
Greetings Steemit friends
Come up with your example similar to float f=7/2; that illustrates the loss (distortion) of value during division. Show how to fix it. Explain why this happens and how you fixed it.
The main challenge is as a result of the data type assigned to the value. As explained in the course, Dividing integer data, will result in integer data. For the case of f=7/2, and another case of f=5/2. The result is not preceded, because both values are integers.
- Problem:
Both operands(5 and 2) are integers and the operation division(/) sees them as integers.
An operation between two integers, results in an integer. This is not the case here, as the result is a float (2.5).
int a=5;
int b=2;
float f=a/b; Problem

- Fix:
It is all about changing the data type for operation and making use of either float or double.
Changing an integer to float is just by adding .0 to the integer. So in our case, 5 changes to 5.0.
Now, 5.0/2 will give us an accurate result with the data type of 2.5.
float a=5.0;
int b=2;
float f=a/b; Fix.

Choose a data type independently and illustrate the limitations of its range: demonstrate the lower boundary (crossing the minimum value) and the upper boundary (crossing the maximum value). Also, demonstrate crossing the boundary during multiplication, explaining the results.
This is an aspect that as a beginner, you seem not to border on or let it cross your mind that data types have limits. You get yourself confused when you are not getting the expected result. I will try to demonstrate my understanding of the limitations of a char data type. I will try to lay emphasis on the boundary range in crossing lower and upper boundaries. As mentioned in the course, all data types have a limit they can go.

For the char data type, it holds two minimum and two maximum values. We have the signed and the unsigned char, as the signed hold from -128 to 127 and the unsigned hold from 0 to 255. Let's display the limits for the char data type to demonstrate the minimum and maximum values.

A situation where boundaries are crossed, starting with the lower boundary. Here we will make use of maxBoundary--, to go below the minimum value. As soon as the minimum limit is reached (-128), any value below the limit is wrapped to the maximum value(127)

Now let's look at the situation where boundaries are crossed, starting with the upper boundary. Here we will make use of maxBoundary++, to go beyond the maximum value. As soon as the maximum limit is reached (127), any value above the limit is wrapped to the minimum value(-128)

In the case that we are carrying a multiplication operation, it is possible to exceed the maximum value. For example, if you have to multiply a value that is exactly the maximum limit, it will lead to an overflow. For this reason, forcing the result to wrap and give us a negative value.
As seen in the demonstrations, whenever a limit is reached. Be it upper or lower, as soon as the boundary is crossed. The result will wrap in the opposite direction of the limit.
Find your own example of 0.1!=0.1, meaning there is a certain value in a variable, but the check shows a different number. Or 0.1+0.2!=0.3. Why is this happening?
This is a situation mostly found when working with float data types. To have a better understanding, make use of floating point numbers. Floating point numbers are stored approximately while minimizing the actual value.

In case 0.1+0.2!=0.3. to be true. We will have to make use of the precise floating point numbers. That way, when the two numbers are added. The result will be an approximation and not equal to 0.3.
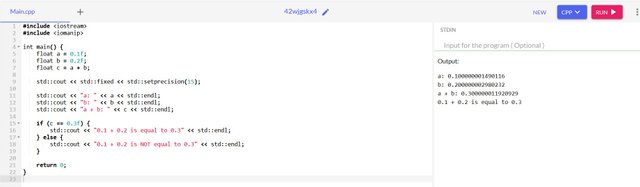
Why do I have to face this situation? Floating point numbers are stored in bits and can not fully represent all the decimal values. If we notice, I set a precision to 15. It can be set to 50, and even more. For this reason, it is highly possible to miss out on the actual value representation of a floating point number.
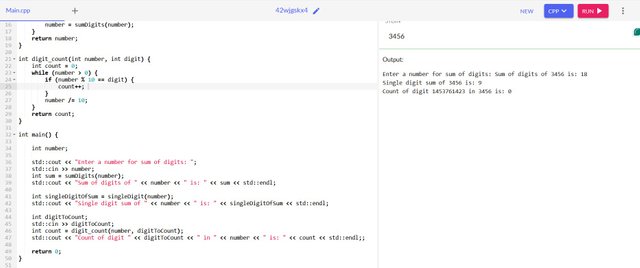
Based on the example of counting digits in a number, write a program that determines:(one of your choice):
- The sum of the digits of a number, (3456 => 3+4+5+6=18), sum(3456) = 18
- The sum of the digits of a number, but finding it for the sum, and for the sum of the sum, until you get a one-digit sum - (3456 => 3+4+5+6=18 => 1+8=9). Here you can do it directly as stated in the task, it won't be the best option, but you can think and find a more efficient solution, which I always ask to find. sum1(3456)=9
- Find the number of a specified digit in a number count_d(143112, 1) = 3, count_d(143112, 5) = 0.
Here, our task required us to calculate the sum of the digits of a number and repeat the calculation to get a single digit. Lastly, specify the digit in the number.
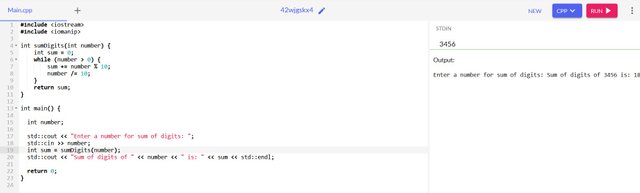
To calculate the sum of the digits, I create a function to handle the logic. Here, the parameter passed (int) with the use of a while loop to extract each digit and accumulate the sum of the digits.
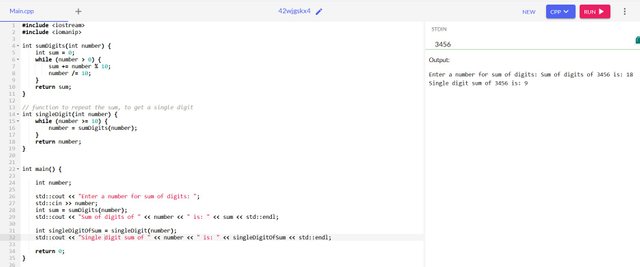
Now, we create a function to repeat the sum until we have a single digit. I made use of the while loop to repeat the sum and drop it from 18(double digit ) to a single digit.
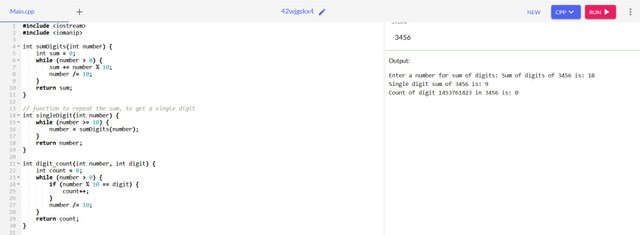
The last section is to get the specific digit and count the number of times a digit appeared.
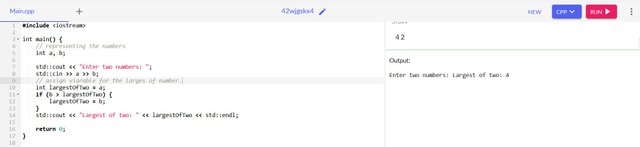
As preparation for the next lesson and to review the past, find the largest of two numbers, then the largest of three numbers (this is a different subtask), then the largest of four, five, six, seven - stop when you understand that you are not following a rational path and for larger quantities, you should do it differently. Complete the task only using the conditional operator if().
This seems a little confusing if I'm actually on track. I will be using the if case for each number.
The largest of two numbers,
The largest of three numbers,
The largest of the four numbers,
The largest of the five numbers,
The largest of six numbers,
The largest of the seven numbers,
To get the largest of each, I will assign a variable as the largest number. Then I will use the if statement to validate if the number is larger than the value in the variable.
- The largest of two numbers
int a, b;
int largestOfTwo = a;
if (b > largestOfTwo) {
largestOfTwo = b;
} return largestOfTwo;
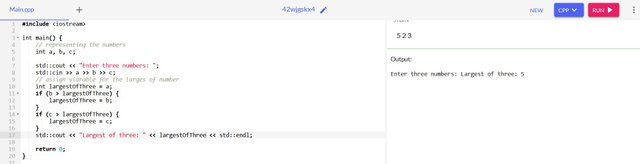
- The largest of three numbers
int a, b, c;
int largestOfThree = a;
if (b > largestOfThree) {
largestOfThree = b;
}
if (c > largestOfThree) {
largestOfThree = c;
}
return largestOfThree;
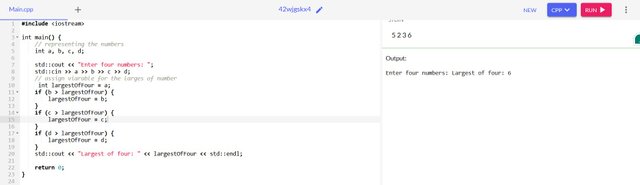
- the largest of four numbers
int a, b, c, d;
int largestOfFour = a;
if (b > largestOfFour) {
largestOfFour = b;
}
if (c > largestOfFour ) {
largestOfFour = c;
}
if (d > largestOfFour ) {
largestOfFour = d;
}
return largestOfFour;
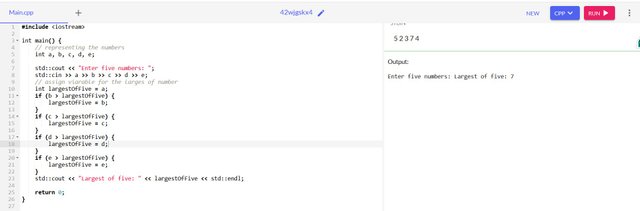
- The largest of five numbers
int a, b, c, d, e;
int largestOfFive = a;
if (b > largestOfFive ) {
largestOfFive = b;
}
if (c > largestOfFive ) {
largestOfFive = c;
}
if (d > largestOfFive ) {
largestOfFive = d;
}
if (e > largestOfFive ) {
largestOfFive = e;
}
return largestOfFive;
- The largest of six numbers
int a, b, c, d, e, f;
int largestOfSix = a;
if (b > largestOfSix) {
largestOfSix = b;
}
if (c > largestOfSix) {
largestOfSix = c;
}
if (d > largestOfSix) {
largestOfSix = d;
}
if (e > largestOfSix) {
largestOfSix = e;
}
if (f > largestOfSix ) {
largestOfSix = f;
}
return largestOfSix;
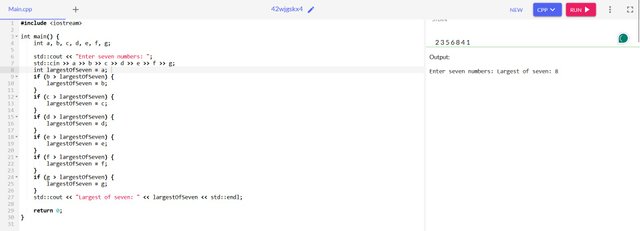
- The largest of Seven numbers
int a, b, c, d, e, f, g;
int largestOfSeven = a;
if (b > largestOfSeven ) {
largestOfSeven = b;
}
if (c > largestOfSeven ) {
largestOfSeven = c;
}
if (d > largestOfSeven) {
largestOfSeven = d;
}
if (e > largestOfSeven) {
largestOfSeven = e;
}
if (f > largestOfSeven) {
largestOfSeven = f;
}
if (g > largestOfSeven) {
largestOfSeven = g;
}
return largestOfSeven;
Perform the previous task using the ternary operator.
To perform the same operation using the ternary operator will be more challenging and long in some cases. I will have to make use of the ternary operator syntax.
(condition) ? if_true : if_false
This is more challenging as we move up to the seven number.
Example
- The largest of Two numbers
int a, b
int largestOfTwo = (a > b) ? a : b;
return largestOfTwo;

- The largest of Four numbers
Here I have to nest ternary operators to be able to get the largest of four.
int a, b, c, d
int largestOfFour = (a > b) ? ((a > c) ? ((a > d) ? a : d) : ((c > d) ? c : d))
: ((b > c) ? ((b > d) ? b : d) : ((c > d) ? c : d));
return largestOfFour;

Here we have a number of conditions to validate to get the largest in the case of four numbers. If a (largest number) is larger than b, that will mean a larger than c, a larger than d, and also true that c is larger than d.
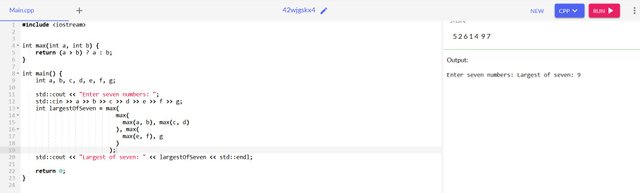
- The largest of Seven numbers
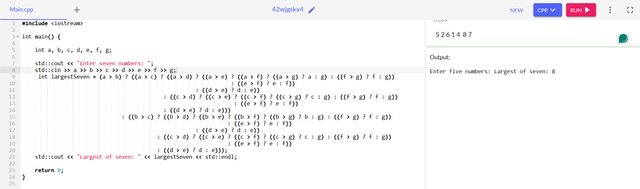
Perform the previous task by writing a function max() and using it.
I used the max() function and passed two parameters(int) using the ternary operator to get the largest number. By nesting the function to get the larger in cases of three, four, five six seven numbers.
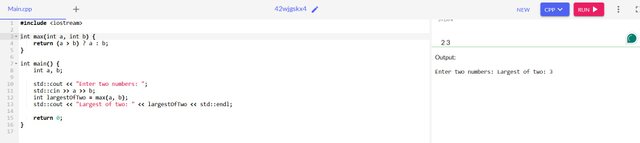
- max() function
int max(int a, int b) {
return (a > b) ? a : b;
}
int a, b;
int largestOfTwo = max(a, b);
largestOfTwo ;
int a, b, c,
int largestOfThree = max(
max(a, b), c
);
largestOfThree ;
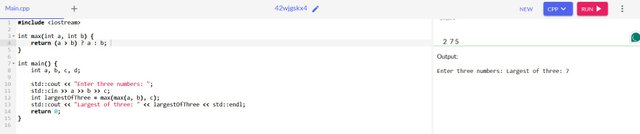
- The largest of Seven numbers
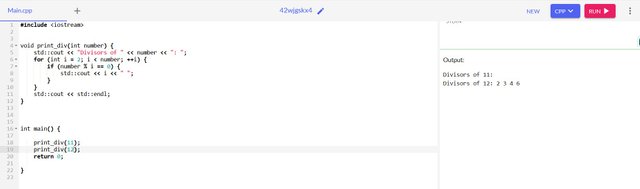
That will print all the divisors of a given number print_div(number) - you can skip printing one and the number itself
print_div(11) => (empty), print_div(12) => 2 3 4 6
Here we use a for loop to iterate through each number from 2 checking if it is greater than 2. If greater than 2, if the division by 2 is equal to zero, then print the value.
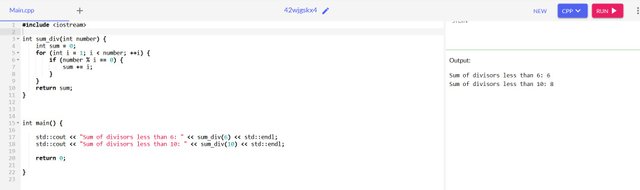
A function sum_div(number) that will calculate the sum of its divisors that are less than itself
sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8
Here the logic is not different from the previous. What we have done is to sum the values after each division.
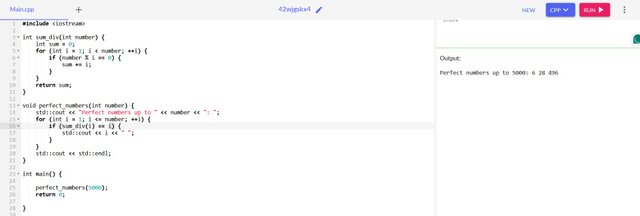
A function that will find and print perfect numbers from 1 to n (the number passed to the function)
Here we will have to make use of the sum_div(number) function above. For every number passed, a check is done using the sum_div(number) function to validate if the number is perfect. If the sum_div(number) is equal to the number, then the number is perfect.
Cheers
Thanks for dropping by
@fombae
Upvoted! Thank you for supporting witness @jswit.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit