
Hello steemians,
Come up with your own example similar to float f=7/2;the one that illustrates the loss (distortion) of value when dividing. But show how to fix it. Explain why this happens and how you fixed it?
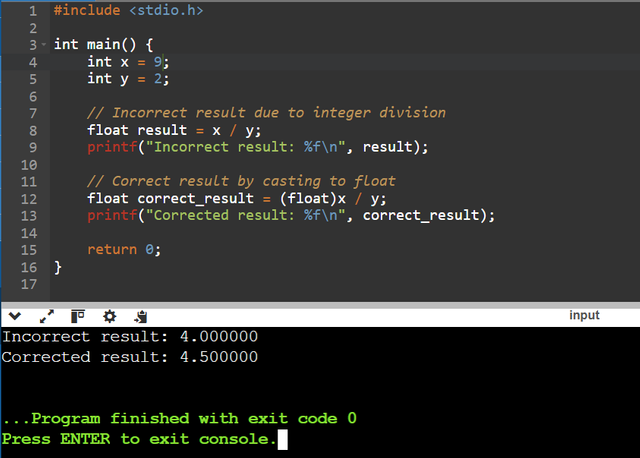
In this example I will explain why dividing 9/2 can produce an unexpected result when I use the float type. Indeed, when I write the instruction float result = x / y; with x defined on 9 and y on 2, the operation takes place in integer division, because in C, as soon as both operands are integers, the calculation is done without taking the decimal part into account. This integer value 4 is then converted to 4.0 when assigned to the result variable of type float which results in a loss of precision compared to the expected result.
To fix this problem and obtain the exact result 4.5, I added a casting operation whose expression is the following (float)x / y which transforms x into a float type only for this operation. By forcing this temporary type change for x I indicate to the compiler that it must treat the expression as a floating point division.
Choose the type of data yourself and illustrate the limitation of its range: demonstrate the limit - from below (transition through the minimum value) and from above (transition through the maximum value. Also demonstrate the transition through the limit during the multiplication operation, explain the results.
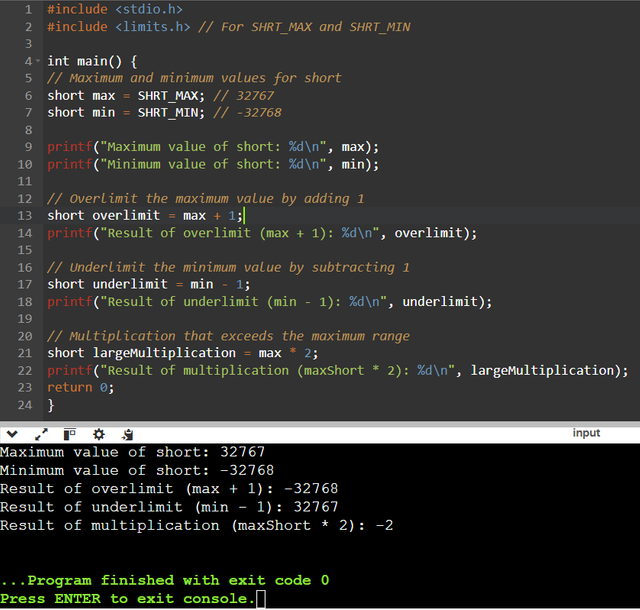
In this code I first define the maximum and minimum values for the short type using SHRT_MAX and SHRT_MIN from the <limits.h> library. The maximum value 32767 is set to max while the minimum value -32768 is stored in min allowing me to monitor the limits of this range via printf.
In our case the overflow is fully explained with the subtype of an integer called "short", starting with the addition of 1 to "max" which is (32767), this bounces the result to -32768, of course since this "short" type has a limited range between -32768 and 32767, also for the subtraction of 1 to "min" (-32768) bounces the value to 32767.
The operation of multiplying "max" by 2 also overflows the result by producing a large negative value. These effects show how calculations outside the range of the "short" type lead to unpredictable results.
Find your analogue that 0.1!=0.1, that is, in some variable, there is a certain value, but the check shows that there is another number. Or 0.1+0.2!=0.3Why so?
Here and in this example I tried to show how the precision of floating point numbers can give unexpected results in C taking the case of 0.1 + 0.2 != 0.3 with the result being close but not exactly equal to 0.3 due to the way floating point numbers are stored in binary.
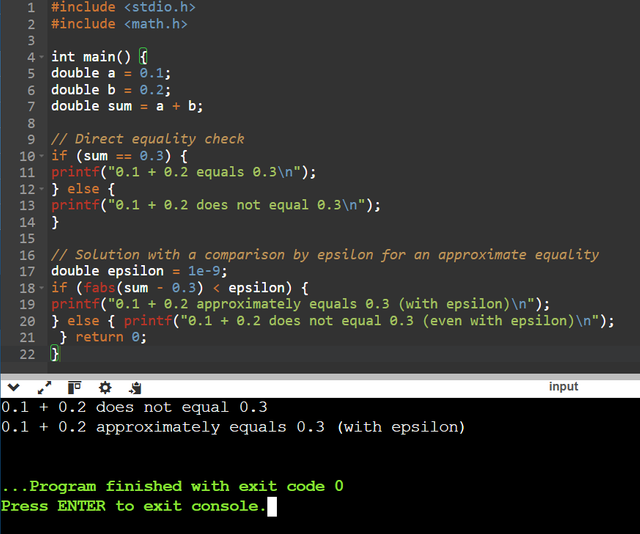
With 0.1 and 0.2 cannot be represented with perfect precision in binary which gives a sum that is close but not exactly equal to 0.3 and the direct check of sum == 0.3 fails because the result is not exactly 0.3 and to find a solution and to solve this problem, I use the approximation that is to say a small margin of error that is called epsilon. So instead of directly checking for exact equality, I will check if the difference between sum and 0.3 is less than epsilon which allows considering the values as "close enough" to be equal.
Based on the example of counting the digits of a number, write a program that finds the number of the specified digit in the number count_d(143112, 1) = 3, count_d(143112, 5) = 0.
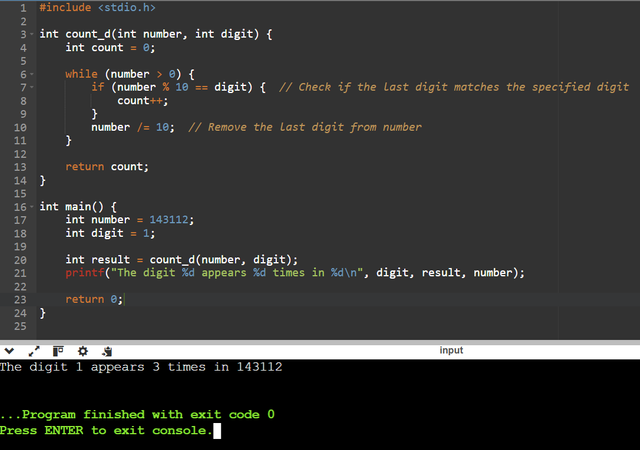

Through this program I started by implementing a function called count_d which takes number and digit as parameters, it initializes the integer variable count to 0 then using the while loop it will go through each digit of number taking the remainder once divided by 10, then if the last digit matches the digit indicated in the parameter count will be incremented by 1 and then the last digit will be removed from number by dividing it by 10. Once all the digits have been checked the function returns count which represents the number of occurrences of the specified digit. For count_digit(143112, 1), the output will be 3, and for count_digit(143112, 5), it will be 0.
As a preparation for the next lesson and repeating the previous one, find the largest of two numbers, then the largest of three numbers (this is another subtask), then the largest of four, five, six, seven - stop at that as soon as you understand that you are not following a rational path and for a larger quantity it should be done differently. The task can only be performed using a conditional operatorif()
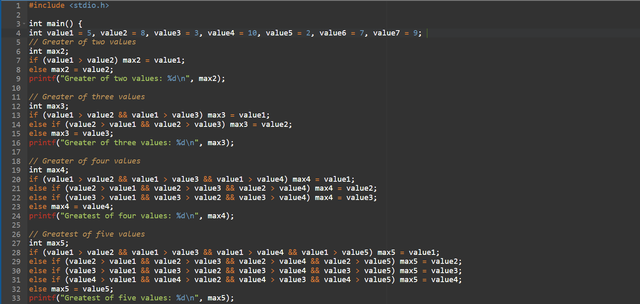
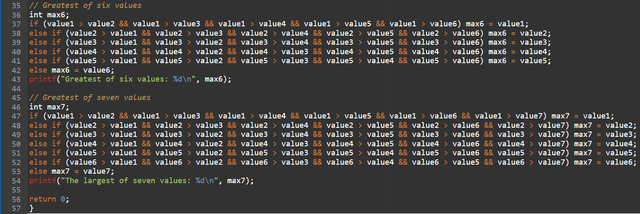
Throughout this example, I used descriptive variable names (value1, value2, etc.). For each combination, I used only the conditional structure to determine the largest number among a set of values.
It can easily be seen that this approach becomes inefficient and difficult to maintain as the number of values increases, i.e. for the combination of two or three values these direct comparisons are reasonably simple however as the values increase to four, five, six, and seven values, the code quickly becomes cumbersome, repetitive and difficult to read.
For larger quantities, it would be more rational to use an array to store the values and to iterate over this array with a loop to find the maximum value.
Perform the previous task through the ternary operator.
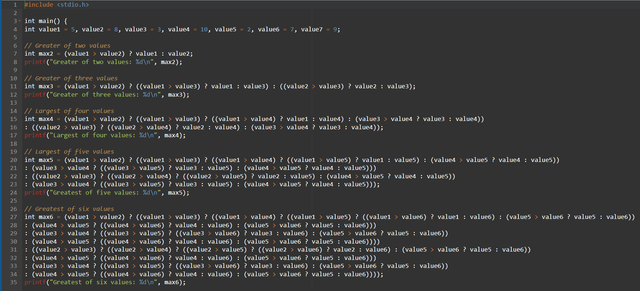
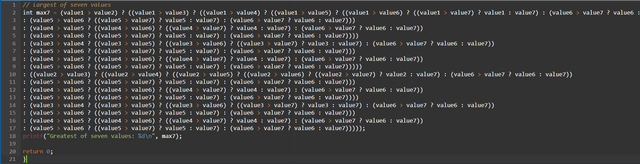
As you can see here using the ternary operator to compare multiple values quickly becomes very complex and difficult to read, because as you increase the number of values the code becomes far too complex to be practical.
Complete the previous task by writing the max() function and using it.
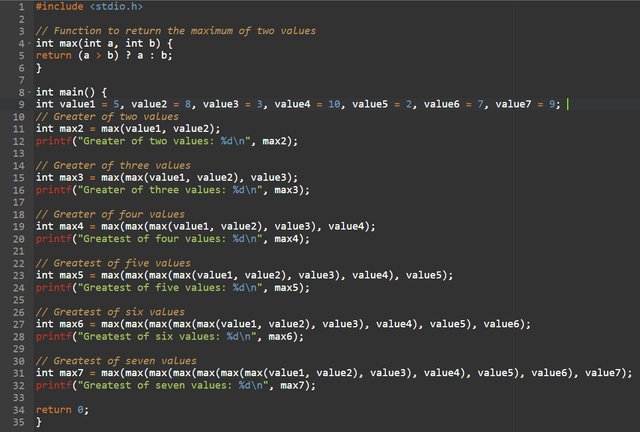
Let's see in this program that with the implementation of the max() function simplifies the code by allowing to find the maximum value only between two numbers and to find the maximum of several values we make nested calls of this function called max(), that is to say to find the maximum of three values we call max(max(value1, value2), value3). This method is more readable and efficient than writing if conditions or ternary operators at each step. However, for a larger number of values, using an array with a loop would be even more convenient.
Write the functions which :
Outputs all the divisors of the specified number print_div(number)- one and the number number itself can not be output
print_div(11) => (empty), print_div(12) = > 2 3 4 6
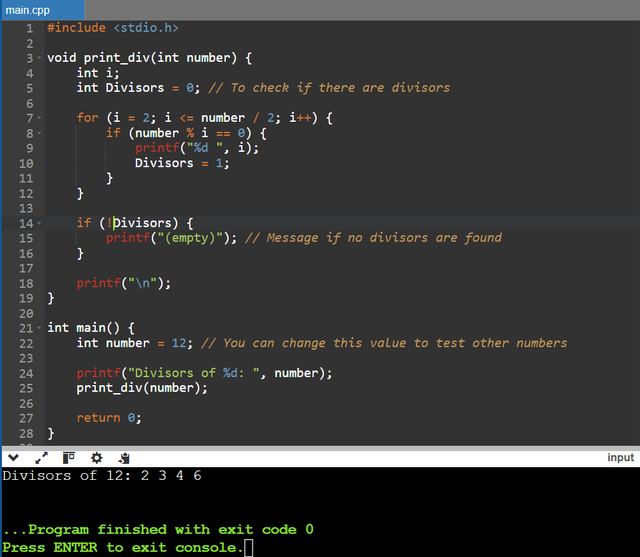
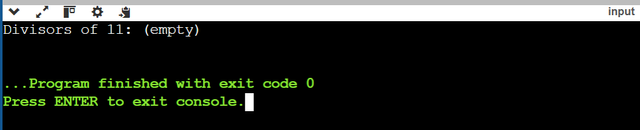
In this program The variable number represents the number whose divisors we want to display, and Divisors is used to check if there are any divisors. For print_div(11), the output will be (empty), and for print_div(12), the output will be 2 3 4 6.
Calculates the sum of its divisors smaller than itself sum_div(6) = 1+2+3=6, sum_div(10) = 1+2+5=8,
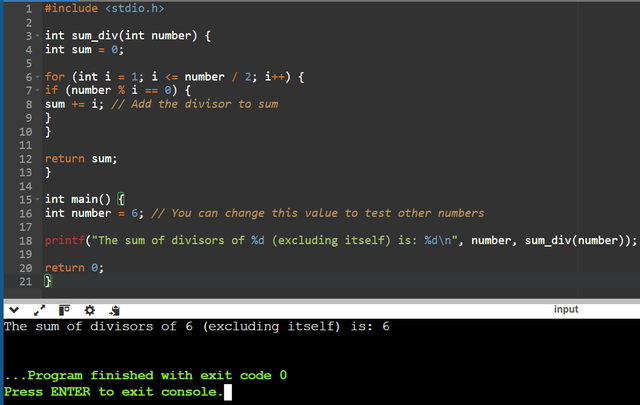

By using the sum_div(int number) function which initializes a variable named sum to 0 and uses the for loop to check all the divisors of number ranging from 1 to number / 2 since any proper divisor of a number is necessarily less than or equal to half of this number, the test is done on the counter i if it is a divisor of number (i.e. number % i == 0) then i is added to sum.
In our example sum_div(6), the result will be 6 since the sum of the divisors 1 + 2 + 3 is 6 on the other hand for sum_div(10), the result will be 8, because the sum of the divisors 1 + 2 + 5 is 8.
Finds and prints perfect numbers from 1 to n (the number passed to the function) perfect numbers are those numbers in which the sum of divisors smaller than the number itself is equal to this number
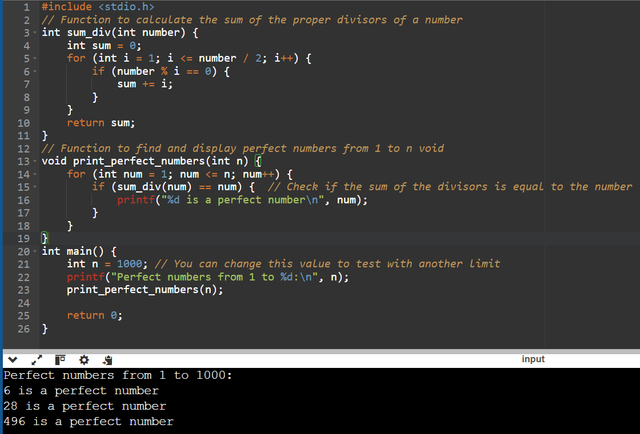
The implementation of the sum_div(int number) function allows to calculate the sum of the proper divisors of a given number, this function is used by the print_perfect_numbers(int n) function to check each number from 1 to n, the test is if the sum of the proper divisors of a number is equal to the number itself, then it is perfect, and the program displays it.
For n = 1000, the program will display 6, 28 and 496 as perfect numbers, because these are the first two perfect numbers in that range (6 = 1 + 2 + 3 and 28 = 1 + 2 + 4 + 7 + 14).
Thank you very much for reading, it's time to invite my friends @cruzamilcar63, @pelon53, @adeljose to participate in this contest.
Best Regards,
@kouba01
