SLC21 Week6 - Programming Games&Puzzles (part 2)

Hello everyone! I hope you will be good. Today I am here to participate in Steemit Learning Challenge of @sergeyk about the Programming Games&Puzzles. It is really an interesting and knowledgeable contest. There is a lot to explore. If you want to join then:

---

---

Join Here: SLC21 Week6 - Programming Games&Puzzles (part 2)

---

---

Designed with ^Canva

What role do random numbers play in the computer world? How can they be transformed from "pseudo-random" to more random?

Random numbers are foundational in modern computing. They provide crucial roles across various domains. Here are different areas where the random numbers play their role:

1. Gaming and Entertainment: Random numbers add unpredictability to gameplay such as random enemy behaviour, loot generation or procedural level design.
2. Cryptography and Security: Random number generate encryption keys, session tokens and authentication codes to ensure secure communication and data protection.
3. Simulations and Modeling: They model real world phenomena such as weather and stock market trends using randomness to account for uncertainty and variability.
4. Machine Learning and AI: Used for dataset splitting, weight initialization in neural networks and stochastic optimization techniques.
5. Optimization and Algorithms: Randomized algorithms like Monte Carlo simulations efficiently solve optimization and probability based problems.
6. Data Sampling and Analysis: Create representative random samples for statistics, polling or A/B testing.
7. Network and Systems Security: Safeguard protocols and applications through random session identifiers, nonce values and port numbers.

---

Transforming "Pseudo-random" Numbers to Truly Random:

Pseudo-random Numbers:

These are generated using algorithms (like rand()) and are deterministic. Given the same seed, the sequence of numbers remains identical, which is useful for reproducibility but can lack unpredictability.

Enhancing Pseudo-randomness:

1. Seeding with Unpredictable External Sources:

   • System time (time(0)): A simple but effective way to introduce randomness by seeding based on the current time in seconds.
   • User inputs or environmental factors: Include mouse movements, keyboard actions, or hardware events for additional unpredictability.

2. Using Advanced Generators:

   • Switch to a higher quality generator like Mersenne Twister or cryptographically secure RNGs, which reduce biases and improve randomness.

3. Incorporating Hardware Randomness:

   • Hardware Random Number Generators (HRNGs) utilize physical phenomena such as thermal noise and quantum events for true randomness.

4. Blending Techniques:

   • Combine pseudo random outputs with entropy from real world sources to mask deterministic patterns.

5. Post processing Techniques:

   • Hashing or scrambling pseudo random sequences removes predictable patterns and enhances randomness.

---

Improving Pseudo-randomness with External Seeding

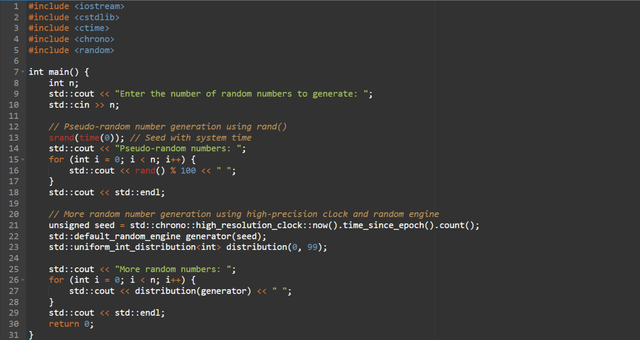
Here is a detailed explanation of the code and how it is working to imrpove the randomness:

• rand():

  • A standard library function that generates pseudo-random integers between 0 and RAND_MAX.
  • Pseudo-random means the numbers follow a predictable sequence determined by the seed.

• srand(time(0)):

  • srand seeds the rand() function with the current time in seconds since January 1, 1970 (Unix epoch).
  • The seed ensures the sequence of numbers varies for different program runs.

• rand() % 100:

  • The modulo operator (% 100) limits the range of generated numbers to 0-99. Without this the numbers could be much larger up to RAND_MAX.

• Output:

  • The for loop runs n times, generating and printing n pseudo-random numbers.

---

More Random Numbers Using High-Precision Seed

• std::chrono::high_resolution_clock::now().time_since_epoch().count():

  • Captures the current time in nanoseconds offering far greater precision than time(0).
  • Converts this time into an integer to use as the seed for the random generator.

• std::default_random_engine:

  • A random number engine provided by the C++ Standard Library.
  • It is more robust than rand() and works well with high-precision seeds.

• std::uniform_int_distribution<int>:

  • Ensures the generated random numbers are evenly distributed within a specific range here the range is 0-99.
  • Unlike rand() % 100 this method avoids potential biases in distribution.

---

How It Transforms Pseudo-random into More Random

1. Pseudo-random (rand()):

   • Depends on time(0) for seeding which has limited precision such as seconds.
   • Numbers generated are deterministic for the same seed and may exhibit patterns if used repeatedly.

2. More Random:

   • Uses nanoseconds as the seed (std::chrono) which increases variability and entropy.
   • std::default_random_engine and std::uniform_int_distribution ensure an even spread of numbers and avoid biases.

This example demonstrates two approaches to random number generation by highlighting how the use of modern libraries and high-precision timing can improve the randomness and distribution quality of generated numbers.

---

---

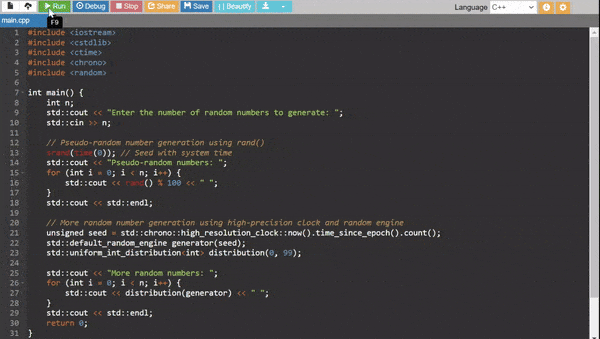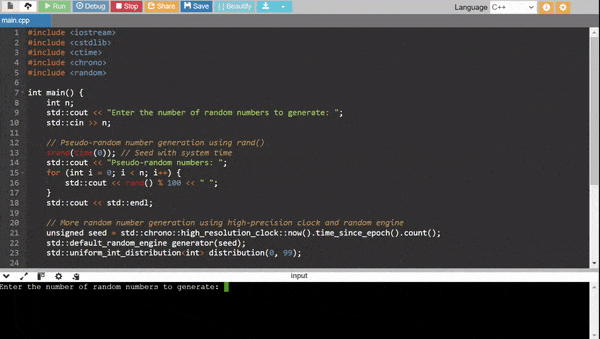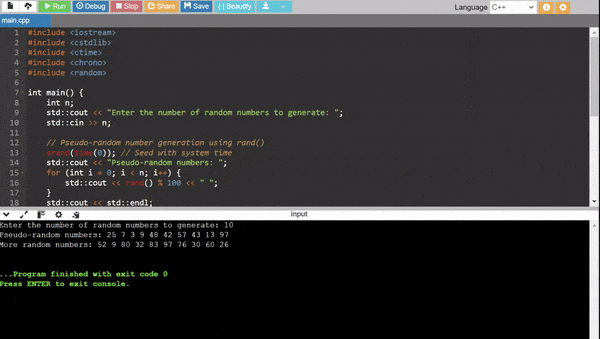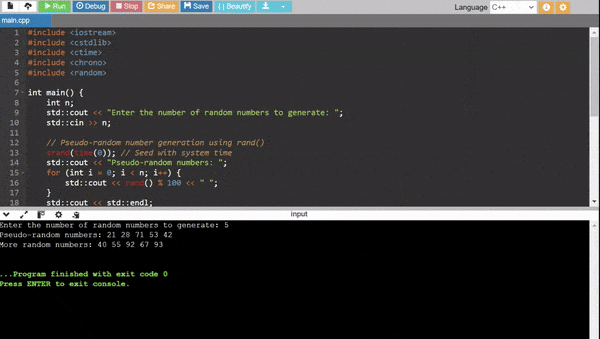
Write a random number generator. Investigate it.

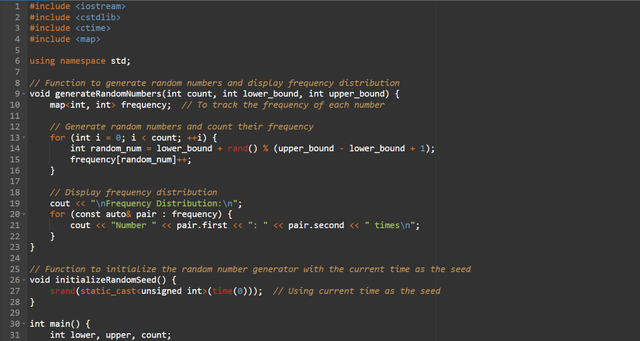
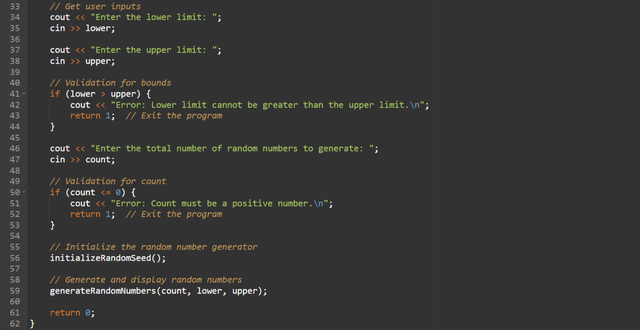
This is a random number generator where the user have to give the upper and the lower limit and the number of the random numbers which the user wants to print.

Moreover this program allows us to investigate the behaviour of the random number generator. Here is how:

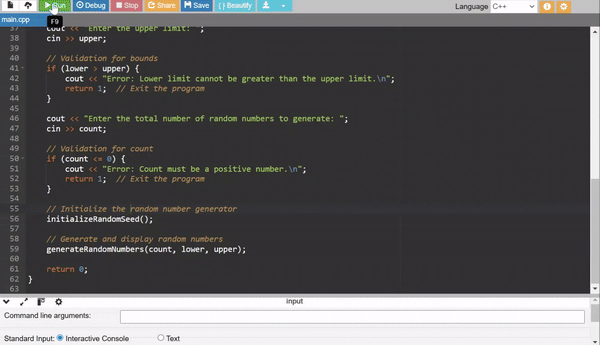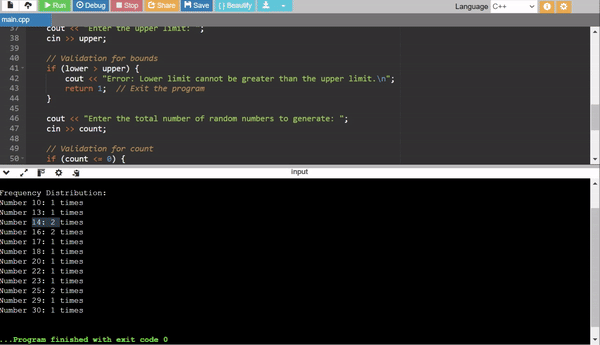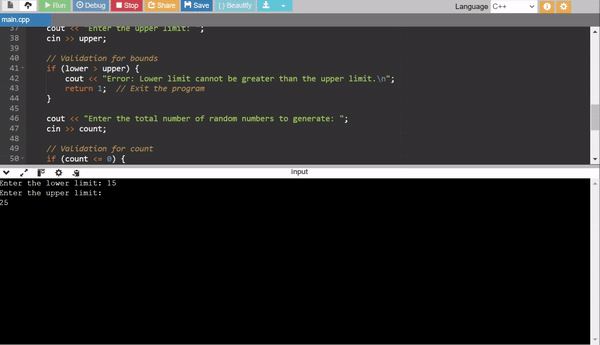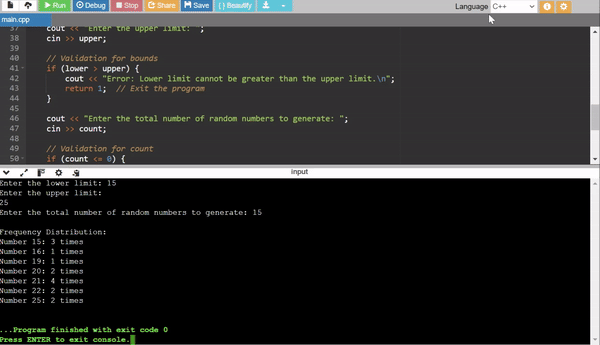
1. Frequency Distribution

• The program tracks how often each number appears within the user specified range (lower_bound to upper_bound).
• Purpose: To identify if the random numbers are evenly distributed such as close to uniform. For a good random number generator all the numbers in the range should ideally have similar frequencies when generating a large number of random numbers.

---

2. Seeding with time(0)

• The function initializeRandomSeed() uses srand(time(0)) to ensure that the random number sequence is different each time the program runs.
• Purpose: Without seeding the random numbers would repeat the same sequence every time the program runs which is not desirable for most applications.

---

3. Ensuring the Range

• The expression rand() % (upper_bound - lower_bound + 1) + lower_bound ensures that random numbers are generated strictly within the user specified range.
• Purpose: This validates that the generator respects user input and does not produce numbers outside the desired range.

---

4. Analyzing Randomness

• Uniformity Test: After running the program, we can check the frequency distribution to see if each number in the range appears roughly the same number of times.
  • Expected Result: Frequencies should be similar for a good random number generator.
  • Example: For a range of 1–5 and 100 generated numbers, we might expect each number to appear around 20 times.

---

5. Brute Force Issues

If the distribution is uneven, it could point to limitations of the rand() function, which may not provide high-quality randomness. For critical applications, a better random number generator like <random> in modern C++ might be required.

---

Key Observations

1. Uniform Distribution:

   • Ideally, the numbers are distributed evenly, but small deviations are expected due to randomness.

2. Seed Impact:

   • Running the program multiple times produces different results because the sequence is seeded with the current time.

3. Range Enforcement:

   • No number outside the specified range appears in the output, ensuring correctness.

4. Limitations of rand():

   • The quality of randomness from rand() is acceptable for general use but may not be suitable for cryptographic or high-precision simulations.

Custom Random Number Generator

• Here in this custom random generator I have used linear congruential generator. The formula of this LCG: Xn+1 = (a × Xn+c) mod m x. After applying this formula the random numbers are generated within a specific range.

• The seed is initialized using time(0) to ensure that the sequence of random numbers changes every time the program runs.

Investigation

Let us analyze the behaviour of the custom random number generator.

1. Uniform Distribution:

   • The random numbers should be evenly distributed across the range [lower_bound, upper_bound]. However, due to the nature of the LCG, slight patterns might emerge in a small number of generated values.

2. Seed Impact:

   • The use of time(0) as the seed ensures that the sequence of random numbers is different every time the program is run. Without a seed, the random numbers would repeat the same sequence in every run.

3. Quality of Randomness:

   • LCGs are relatively simple and fast, but their randomness is not as high-quality as more sophisticated methods, such as those found in the C++ <random> library.
   • For high-stakes applications, such as cryptographic systems or complex simulations, a better random number generator should be used.

---

---

"Deck of Cards" - Find several ways to fill the array 1...N - 1.

Here are five different methods to solve the "Deck of Cards" problem, where the goal is to fill an array with unique numbers from 1 to N - 1:

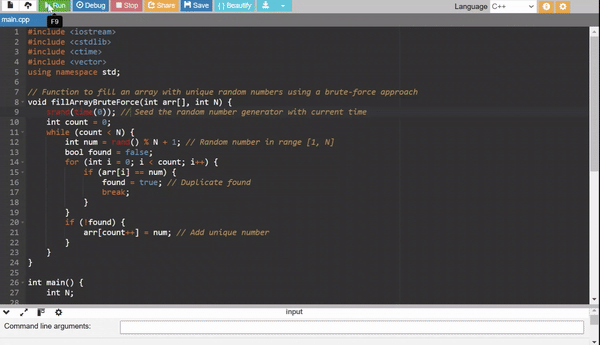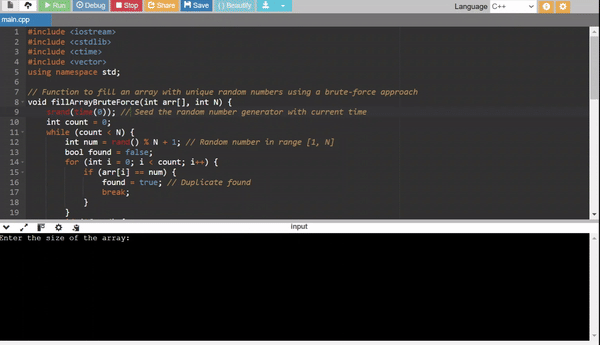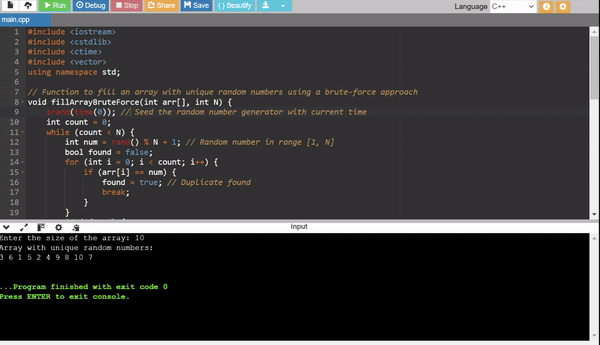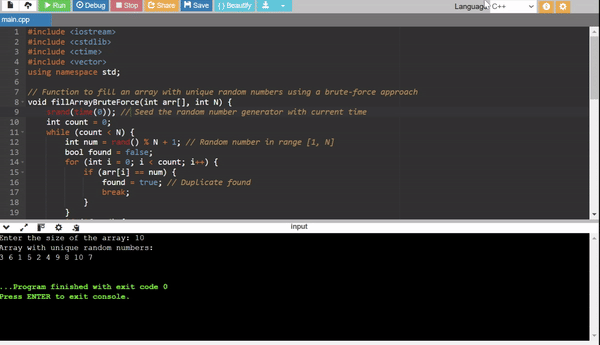
Method 1: Brute Force Method

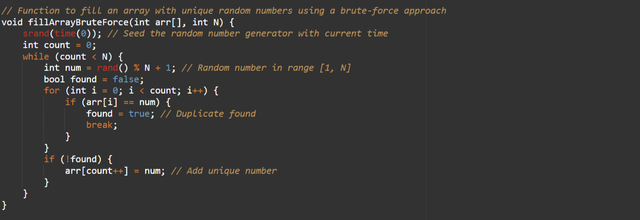
1. Generate random numbers and add them to the array only if they are not already present.
2. Check for uniqueness in every step, which makes it inefficient for large (N).

Efficiency:

• Time Complexity: (O(N^2)) (due to the repeated duplicate checks).
• Use Case: For small values of (N).

---

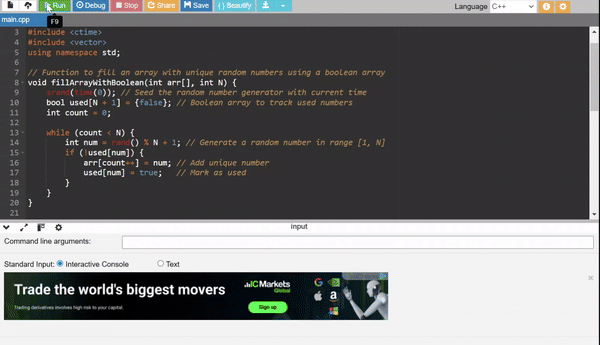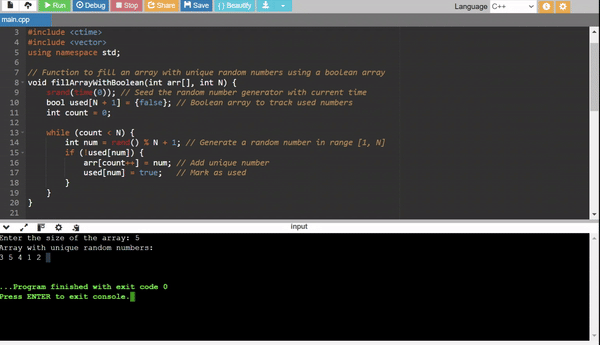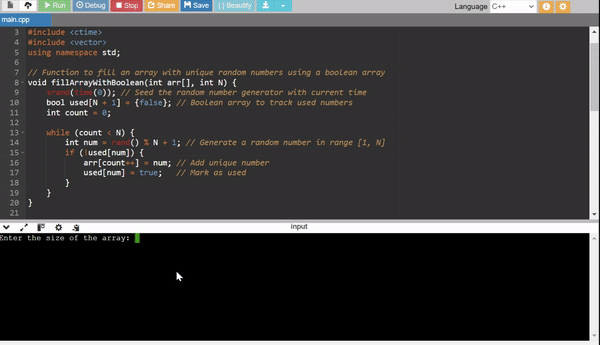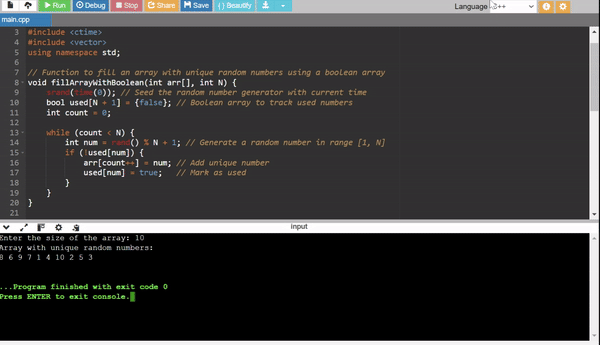
Method 2: Using a Boolean Array for Uniqueness

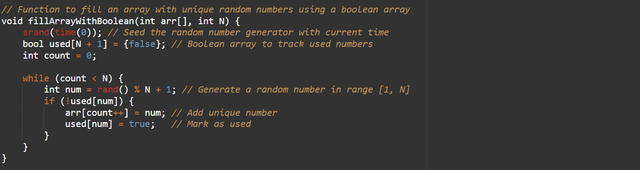
1. Use a boolean array to track whether a number has already been added.
2. Efficiently skip duplicates during generation.

Efficiency:

• Time Complexity: (O(N)) for small (N) but still depends on the randomness of the generator.
• Space Complexity: (O(N)) for the boolean array.

Method 3: Shuffle the Array

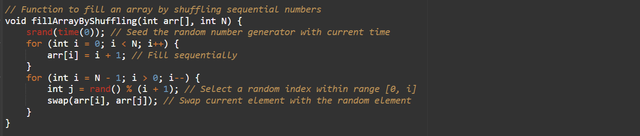
1. Fill the array sequentially with (1, 2, ..., N).
2. Shuffle the array using the Fisher-Yates shuffle algorithm.

Efficiency:

• Time Complexity: (O(N)) (optimal for shuffling).
• Use Case: When shuffling is allowed.

---

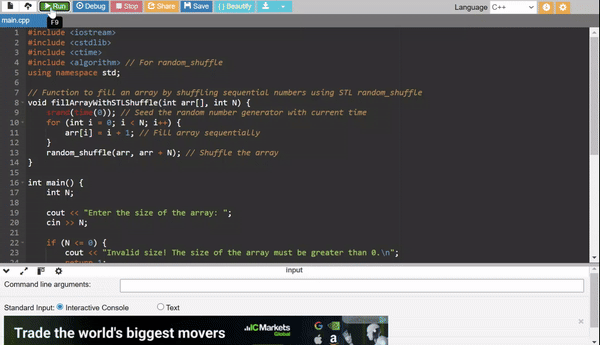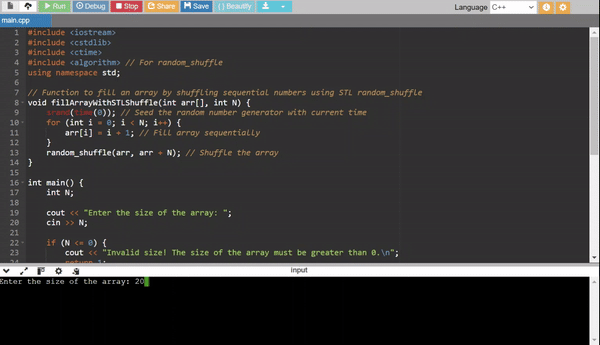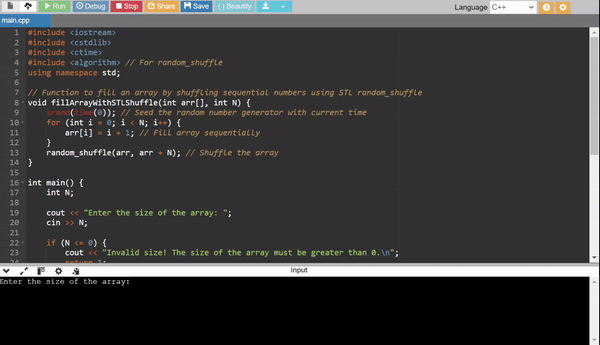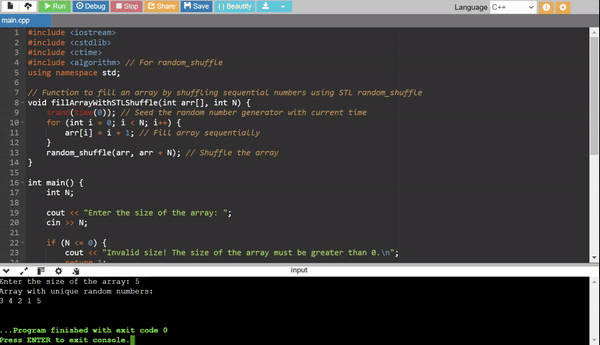
Method 4: STL Random Shuffle

This method uses the C++ Standard Library to shuffle a pre-filled array.

Efficiency:

• Time Complexity: (O(N)) for shuffling.
• Use Case: Quick implementation using STL.

---

Method 5: Use a Set to Ensure Uniqueness

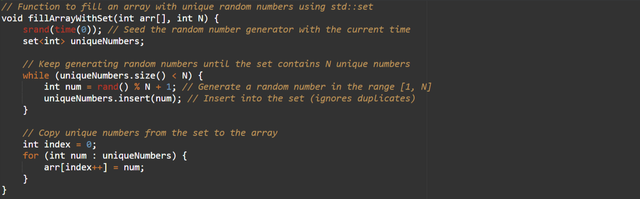
1. Use a set to store only unique numbers.
2. Populate the array from the set.

Efficiency:

• Time Complexity: (O(N log N)) due to set operations.
• Use Case: When ensuring uniqueness without manual checks.

---

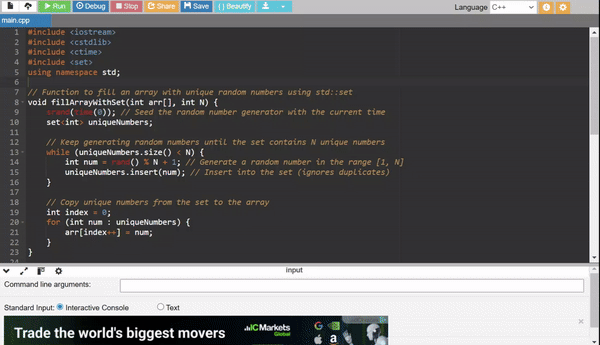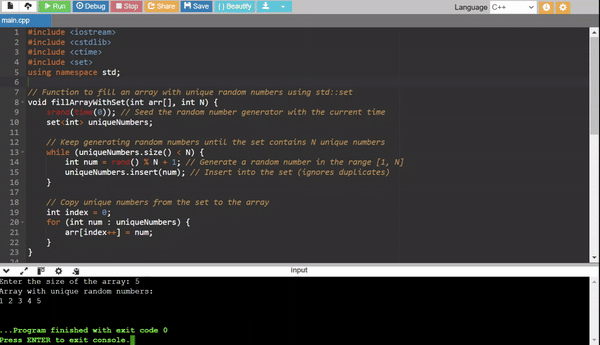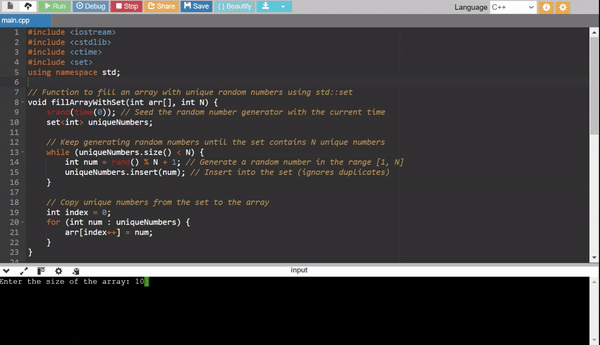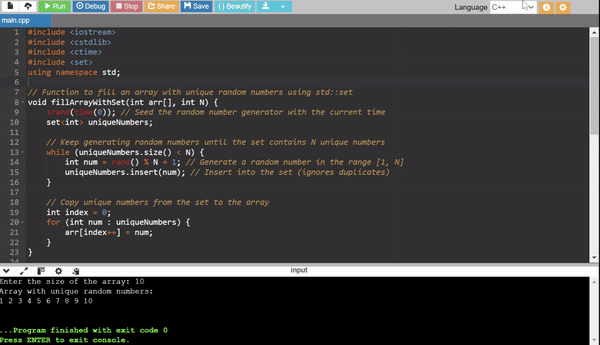
Summary of Methods:

Method	Time Complexity	Key Concept
Brute Force	O(N^2)	Check for duplicates manually
Boolean Array for Uniqueness	O(N)	Track used numbers with a boolean
Fisher-Yates Shuffle	O(N)	Shuffle a sequential array
STL random_shuffle	O(N)	Use STL to shuffle
Set for Uniqueness	O(N log N)	Use a set to eliminate duplicates

Each method has its own characteristics in terms of time and space complexity. We can choose based on the constraints and (N)'s size.

---

---

Construct a table of the number of operations required to generate a deck of N cards for your methods.

Here is an analysis of the number of operations for generating a shuffled deck of N cards. I will do these analysis based on the different methods which I have recently used in the previous question as well. The number of operations is based on the time complexity and assumptions about the key operations involved like checking for duplicates or swapping elements.

Assumptions

1. Brute Force: For every number added to the array, on average, half of the current numbers in the array are checked for duplicates.
   • Operations: O(N^²) (quadratic growth).
2. Boolean Array for Uniqueness: Checking and marking uniqueness is O(1)for each number so it's proportional to N.
   • Operations: O(N).
3. Fisher-Yates Shuffle: Requires a single swap operation for each number in the array.
   • Operations: O(N).
4. STL random_shuffle: Similar to Fisher-Yates shuffle, it's O(N).
   • Operations: O(N).
5. Set for Uniqueness: Adding to a set involves O(log N) for each insertion, so total operations are O(N log N).

---

Table of Operations

Ncards	Brute Force (Approx N^2)	Boolean Array (Approx N)	Fisher-Yates Shuffle (Approx N)	STL Shuffle (Approx N)	Set Method (Approx N log N)
5	25	5	5	5	12
10	100	10	10	10	33
20	400	20	20	20	86
50	2,500	50	50	50	282
100	10,000	100	100	100	664
200	40,000	200	200	200	1,520
500	250,000	500	500	500	4,491
1,000	1,000,000	1,000	1,000	1,000	9,966

---

Explanation

1. Brute Force:

   • Quadratic growth as N increases. It is inefficient for larger decks.
   • Example: For N = 20, ~400 operations, but for N = 1000, it explodes to ~1,000,000.

2. Boolean Array:

   • Linear growth. Each number requires a constant check and insertion so it is proportional to N.
   • Example: N = 50, 50 operations.

3. Fisher-Yates Shuffle:

   • Linear growth. Each number is swapped once, making it very efficient.
   • Example: N = 200, 200 operations.

4. STL Shuffle:

   • Linear growth similar to Fisher-Yates. Internally uses efficient algorithms to shuffle.
   • Example: N = 500, 500 operations.

5. Set Method:

   • Logarithmic overhead due to insertion into a set. Total operations grow as (N log N).
   • Example: For (N = 200), the logarithmic factor leads to 1,520 operations.

---

Observations

• The Boolean Array, Fisher-Yates Shuffle and STL Shuffle are the most efficient for generating decks of cards.
• The Brute Force method is computationally expensive and should only be used for small N.
• The Set Method provides a balance between simplicity and efficiency especially for moderate sized decks.