
La Serie Computación y Programación en su primera edición, consiste en una entrega diaria, donde hablaremos de un tema, en la misma abordaremos los aspectos teóricos, describiremos algunos ejemplos con el objetivo de visualizar y explicar como aplicar lo tratado durante la publicación. La misma está dirigida al público en general, pero con especial atención a estudiantes universitarios, que deseen estudiar o estudien computación, ingeniería en computación y carreras afines. Estoy abierto a sus comentarios y dudas que puedan surgir en el desarrollo del mismo. Sin perder más tiempo, iniciemos.

Construcción de números en diferentes bases
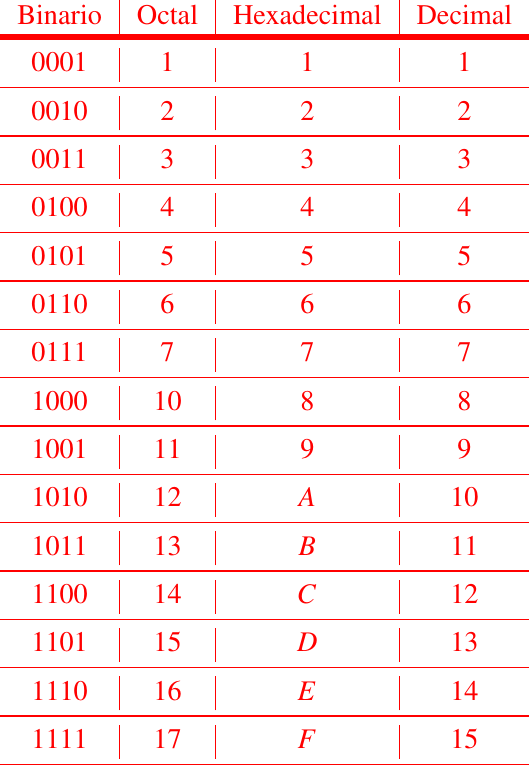
Como ya en anteriores post mostramos la Tabla de equivalencias de algunos números en las bases: binaria, octal, hexadecimal y decimal, para ser más específicos los primeros 15 números. Entonces surge la siguiente pregunta natural:
¿como se forman números consecutivos mayores que el representado por su mayor símbolo individual?
Si tomamos el sistema de representación numérica decimal, el número más grande que se puede formar, con un solo dígito, es nueve. Si queremos representar números mayores que nueve entonces se utiliza más de un dígito, como podemos ver a continuación:

Como podemos apreciar, una vez escritos todos los dígitos simples, se forman todas las combinaciones de dos dígitos comenzando con 1, luego se forman las combinaciones de dos dígitos comenzando con 2 y así sucesivamente hasta llegar al 99. Posteriormente una vez terminadas todas las posibles combinaciones de dos dígitos se procede a formar las combinaciones que tienen tres dígitos; luego se continúa con todas las combinaciones de cuatro dígitos y así sucesivamente.
Este proceso se puede continuar por siempre y se puede aplicar de manera similar a otros sistemas numéricos.
Ahora bien, si queremos formar números mayores que 7 en el sistema octal se utiliza la regla de formación similar a la que se uso en la Tabla (la cual hemos mostrado anteriormente) siguiente:

Ejemplo 01: En el sistema hexadecimal, ¿cómo se forman los números mayores que F?
Para formar números mayores que F, la manera de realizarlo es similar a la que presentamos o la manera natural de realizarlo con el sistema decimal, recordando que los símbolos de la base hexadecimal, son:
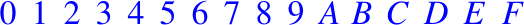
Así, entonces podemos formar los números mayores que F, como los mostramos a continuación:
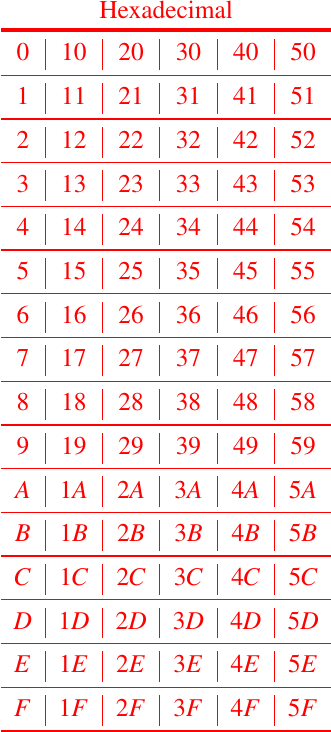
y podemos continuar infinitamente, al igual que en el caso de la base decimal.
Observemos que, primero escribimos la secuencias de todos los dígitos simples, luego se forma todas las combinaciones posibles con dos dígitos simples, comenzando con 10 y terminando con el dígito FF. Así, cuando se agotan las secuencias de dos dígitos, se forman las combinaciones de tres dígitos, que empiezan con 100 y terminan con FFF. Este proceso se repite con todas las combinaciones de cuatro dígitos y así sucesivamente, indefinidamente.
Ejemplo 02: En el sistema octal, ¿cómo se forman los números mayores que 8?
De manera similar que el ejemplo anterior, formaremos los números mayores que 8 en la base octal, como lo vemos a continuación:

y podemos continuar infinitamente, al igual que en el caso de la base decimal y hexadecimal.


Queridos amigos y lectores, espero hayan disfrutado de este cuarto post de la serie de Computación y Programación, de igual manera los invito para la próxima entrega de esta serie, donde continuaremos tratando este tan bonito tema de los sistemas de numeración y otros aspectos. Espero que esto pueda servir de apoyo a ustedes, hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la computación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias.
- Knuth, Donald Ervin. The art of computer programming. Vol. 1, 2, y 3. Pearson Education, 1997.
- Knuth, Donald Ervin. Fundamental algorithms: the art of computer programming. 1973.
- Knuth, Donald Ervin. Computer programming as an art. ACM Turing award lectures. ACM, 2007.
También los invito a leer las anteriores publicaciones de está serie de Computación y Programación, que estoy seguro serán de su interés:
| Sistemas de Numeración #1 | Sistemas de Numeración #2 | Sistemas de Numeración #3 |
|---|
Todas las ecuaciones fueron creadas y editadas por @abdulmath con  , y GIMP.
, y GIMP.

Imagen elaborada por @abdulmath, diseñadas y editada con Karbon y GIMP.
Hola profe @abdulmath lo sigo con interés, me agrada leerlo e ir aprendiendo. No es fácil explicar un tema de matemáticas con tanto detalle, se nota su esfuerzo. Felicidades.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @carmenmdm, gracias por tu comentarios y visitar mi blog. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Nuevamente buen aporte @abdulmath, espero que el publico Steemit, en especial los estudiantes universitarios interesados, aprovechen el contenido. Saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Agradecido @lupafilotaxia, por tu comentario. En realidad, espero que mis publicaciones puedan ser de ayuda a todos los interesados en aprender con estos temas que trato. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Como siempre nos traes una serie presentada con hermosa elegancia. Mis respetos. Profe.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @rmartinezpoeta, muy agradecido por tu apreciación. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @abdulmath te sigo con detenimiento. Fe licitaciones por tu trabajo y por comunicar información de valor agregado para este hermoso océano de información.
Buena vibra.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @angelica7, gracias por tu comentario. La idea es esa, dar un pequeño aporte en la medida de lo que me lo permitan mis posibilidades. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Feliz dia.... que complejos son los números pero que útiles, me hiciste recordar porqué no estudié matématicas... a pesar de siempre haber estado rodeada por ellas... felicitaciones por tu manera de explicar
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @vidaparasita, gracias por tomarte el tiempo de leer mi publicación, agradecido por tu comentario, importante siempre, bueno aún estas a tiempo de aprender poco a poco con mis series de publicaciones, te invito a hacerlo, es muy sencillo. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
hola profe
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @duque
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @abdulmath, los ejemplos de base hexadecimal y base octal bien presentado.
Un Abrazo
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @henjos, que bueno que te gustará mi publicación. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit