Fuente
Para deducir las funciones trigonométricas del ángulo de 45°, inscribamos un cuadrado dentro del círculo trigonométrico de radio r=1, de tal forma que uno de los vértices del cuadrado coincida con el centro del círculo O = (0,0) y su vértice opuesto sea el punto sobre el círculo B = (p,p). Los demás vértices del cuadrado son A = (p,0) y C = (0,p).
Tómese en cuenta que al unir los vértices O y B, se obtiene la diagonal del cuadrado OABC que coincide con el radio r=1 del círculo. Además se forman dos triángulos rectángulos, ellos son ∆OAB (triángulo OAB) y ∆OCB (Triángulo OCB) cuya hipotenusa “h” coincide precisamente con el radio del círculo, y a la vez con la diagonal del cuadrado, por lo tanto h=1.
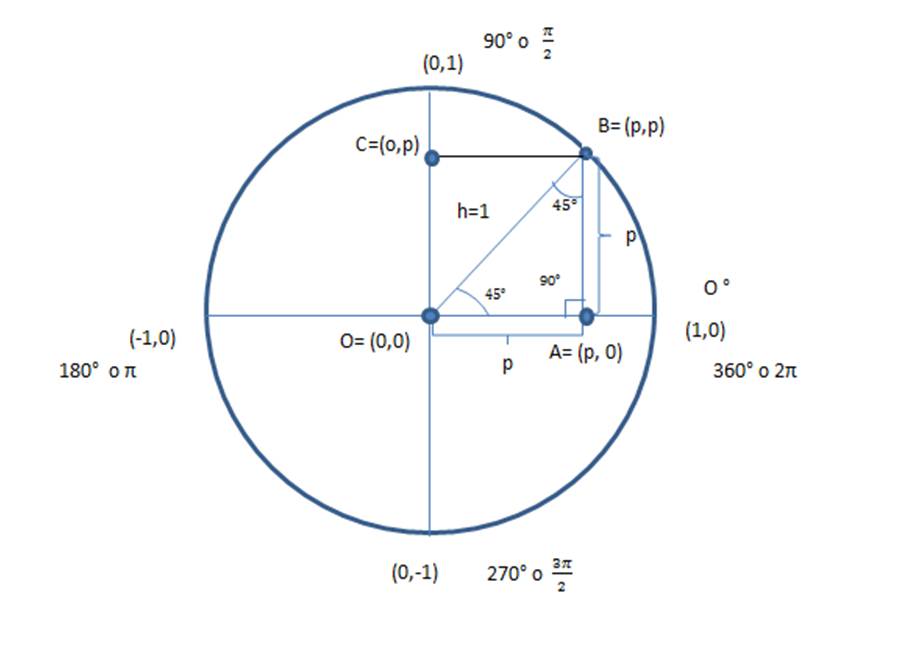
Centremos nuestra atención en el ∆OAB, los ángulos AOB y OBA son ángulos de 45°, ya que la diagonal “h” bisecó los dos ángulos rectos del cuadrado OABC. Trabajemos con uno de ellos para definir las funciones trigonométricas del ángulo de 45°, específicamente con el ángulo AOB.
Para ello, utilicemos el teorema de Pitágoras para determinar la longitud de los lados del dicho triangulo.
De acuerdo a este teorema la longitud de la hipotenusa al cuadrado es igual a la suma de los cuadrados de los lados. La hipotenusa de nuestro triángulo es h=1, la longitud de ambos catetos son iguales a p (recuerde que son los lados de un cuadrado), de donde:
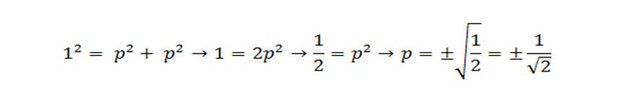
Escogemos el resultado positivo ya que se trata de la longitud de un segmento, luego racionalizamos, en este caso voy a multiplicar tanto el numerador como el denominador por √2, de la siguiente manera:
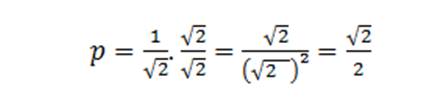
De tal forma que p=√2/2
Con este resultado podemos ahora definir las funciones trigonométricas del ángulo de 45°.
| Función | Valor |
|---|---|
| Seno | √2/2 |
| Coseno | √2/2 |
| Tangente | 1 |
| Cosecante (Recuerde que la cosecante es el valor inverso del seno) | 2/√2.(√2/√2)=(2√2)/2=√2 |
| Secante (Valor inverso del coseno) | 2/√2.(√2/√2)=(2√2)/2=√2 |
| Cotangente( Valor inverso de la tangente) | 1 |