Estudio del cálculo: Límite y continuidad de funciones reales. Parte I

En esta oportunidad quiero dar un especial saludo a las comunidades de #cervantes, #entropia, #proconocimiento, #steemstem, #stem-spanol y #utopian-io por su engrandecido apoyo a las publicaciones de habla hispana orientadas al contenido científico y académico, en donde se valora el aporte en las ramas de matemática, química, física, biología y educación.

En esta oportunidad sigo en la temática del estudio del cálculo, en lo referente a Límite y continuidad de funciones reales. Ya para llegar a estudiar los límites de funciones reales debemos de comprender el estudio sobre funciones reales y matemáticas previas al cálculo:

• Matemáticas previas al cálculo

• Estudio del Cálculo: Funciones reales. Parte I y II:

Parte I

ParteII

El estudio sobre el límite de funciones reales es el universo donde se separa el mundo sin cálculo con el mundo con cálculo, para ello es necesario realizar una síntesis sobre el acercamiento de estos dos mundos.

Surge una gran interrogante para entender lo que acontece en el mundo donde no existe el cálculo:

¿Qué es el cálculo?

Una manera sencilla de entender lo que es el cálculo, es ver el cálculo como aquella máquina capaz de transformar fenómenos dados en nuestra naturaleza donde existan cambios, estos fenómenos de cambios se suelen expresar de diversas formas, un ejemplo de fenómenos de cambios son la velocidad y la aceleración. No solamente la velocidad y la aceleración son objetos de estudio del cálculo, sino también el cálculo de las rectas tangentes, pendientes, áreas, volúmenes, longitudes de arco, centroides, curvaturas y una gran variedad de conceptos que han permitido a científicos, ingenieros y economistas a elaborar modelos matemáticos basados en las esencias del cálculo infinitesimal para poder dar respuestas en algunos problemas reales en el área de la ciencia, ingeniería y economía.

De los muchos problemas que trata el cálculo se pudiera interpretar que pudieran ser resueltos con la ayuda de la matemática clásica, ya que estas también tratan con velocidades, aceleraciones, rectas tangentes y pendientes, sin embargo existe una diferencia fundamental entre las matemáticas sin cálculo y el cálculo. La diferencia más marcada entre ambas es que las matemáticas sin cálculo son más estáticas, mientras que el cálculo es más dinámico. Para comprender esta comparación, establezcamos una serie de ejemplos que ayudará a comprender las diferencias entre el cálculo y las matemáticas sin cálculo:

• Las matemáticas sin cálculo permiten analizar un objeto que se mueve con velocidad constante. Sin embargo, para analizar la velocidad de un objeto sometido a aceleración es necesario recurrir al cálculo.

• Las matemáticas sin cálculo permiten analizar la pendiente de una recta, pero para analizar la pendiente de una curva es necesario el cálculo.

• Las matemáticas sin cálculo permiten analizar una recta tangente a un círculo, pero para analizar una recta tangente a una gráfica en general es necesario el cálculo.

• Las matemáticas sin cálculo permiten analizar el área de un rectángulo, pero para analizar el área bajo una curva general es necesario el cálculo.

Autor: HiTe el cual ha liberado la imagen al dominio público.
Fuente de imagen

¿En qué modo interviene el concepto de límite en el proceso transitorio entre la matemática y el cálculo?

El proceso transitorio entre la matemática clásica y el cálculo se da mediante un modo donde se pueden utilizar una serie de estrategias generales donde se utiliza la reformulación de las matemáticas previas al cálculo a través de un proceso llamado"Límite". En base a esta concepción podemos conceptualizar al cálculo bajo el enfoque de límite, siendo así entonces podemos decir que el cálculo es una máquina de límites que funciona en tres etapas:

• La primera la constituyen las matemáticas previas al cálculo, con nociones como la pendiente de una recta o el área de un rectángulo.

• La segunda es el proceso de límite.

• La tercera es la nueva formulación propia del cálculo, en términos de derivadas e integrales.

Lamentablemente la forma en la que muchas veces se aprende cálculo no va dirigido a la comprensión de este proceso transitorio, sino por el contrario como si su estudio y aprendizaje se tratara de una forma de recopilar un cúmulo de fórmulas, es una situación muy grave ya que si todo el estudio del cálculo se reduce a la memorización de fórmulas de derivación e integración, su comprensión será deficiente, el aprendiz entonces perderá la confianza necesaria en sí mismo y no obtendrá satisfacción por el nuevo aprendizaje en el gran universo del cálculo.

El problema de la recta tangente

La noción de límite es fundamental para el estudio y entendimiento del cálculo, es por ello que se explicaran dos problemas que dieron paso al mundo del cálculo, estos dos problemas son: el problema de la recta tangente y el problema del área, los dos problemas muestran la forma en que intervienen los límites en el cálculo.

Para el problema de la recta tangente, tenemos la siguiente situación: tenemos una función f y un punto P, en donde se trata de encontrar la ecuación de la recta tangente a la gráfica en el punto P, tal y como se muestra en la siguiente imagen: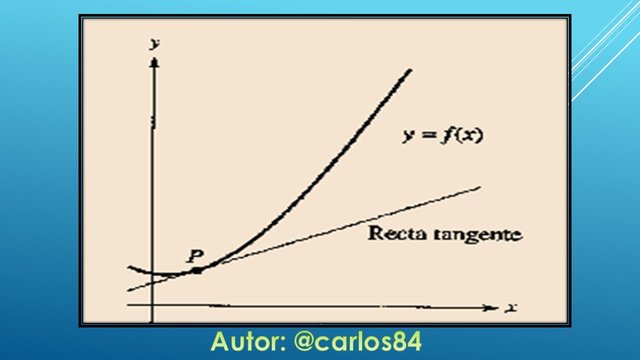

El problema de encontrar la recta tangente en el punto P equivale a determinar la pendiente de la recta tangente en P. La pregunta inmediata entonces es:

¿Cómo se puede calcular la pendiente de la recta tangente que pasa por el punto P?

La pendiente de la recta tangente que pasa por el punto P se puede calcular aproximadamente trazando una recta por el punto de tangencia y por otro punto sobre la curva (recta secante). Tal como se muestra en la siguiente imagen:

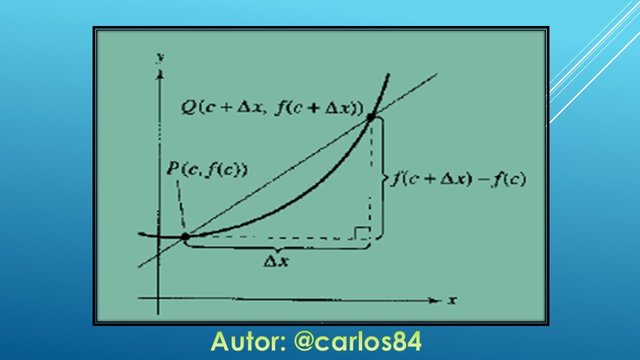
Los dos puntos que delimitan la recta que es secante a la curva son P y Q, estos puntos tienen las siguientes coordenadas (x,y):

P(c,f(c))
Q(c+∆x,f(c+∆x))

Si suponemos q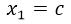ue y que 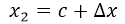, ya tendríamos las coordenadas de X de los dos puntos de la recta secante. Para las coordenadas en Y tendríamos que 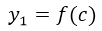y .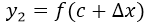

Si utilizamos la ecuación de la pendiente (m) de una recta, diríamos que 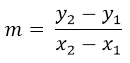; sustituyendo los valores de la ecuación nos quedaría que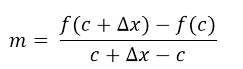

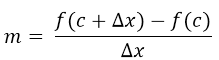⇒ , el problema de esta ecuación es que solamente se puede aplicar si se conocen dos puntos de la recta es decir solamente cuando la recta es secante. De allí surge la siguiente interrogativa:

¿Se puede calcular la pendiente de una recta si se conoce un solo punto?

Para responder a esta pregunta, primero tenemos que estar conscientes de que, para que se calcule la pendiente de la recta conociendo un punto, es porque ese punto que se conoce es el de tangencia a la función, por lo que primeramente se debe considerar que la recta no sea tangente a la curva f(x), sino más bien secante a la función. Para que la recta sea secante a la función solo se conoce el punto que es tangente, entonces se debe considerar otro punto arbitrario sobre la curva. El inconveniente surge es debido a que el otro punto es arbitrario, es decir es desconocido, por lo que la propuesta que se plantearon Leibniz y Newton en su época fue el de acercar al punto arbitrario lo más que se pudiese al punto tangencial, tanto que pareciera que es un solo punto. Bajo esta premisa surge otra interrogante:

¿Mediante qué análisis se puede acercar el punto arbitrario al punto tangencial?

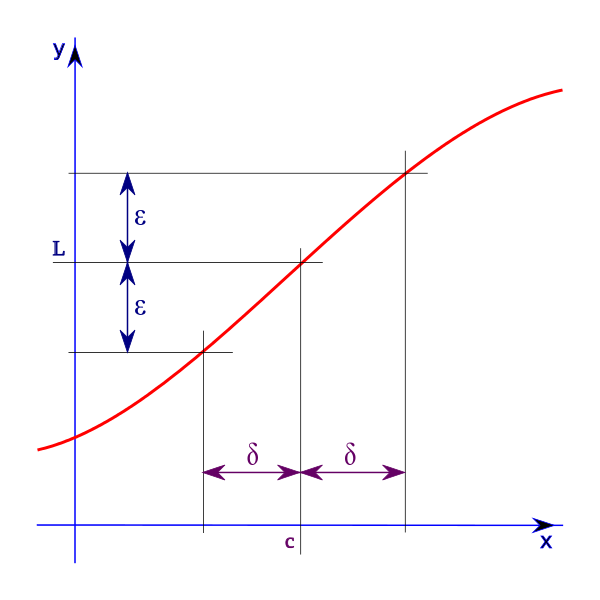
La única forma de llegar a juntar dos puntos que se encuentran separados y ponerlos muy cercas pero que no se junten, es mediante el concepto de lo que hoy en día conocemos como límite, es un concepto que es común en nuestro cotidiano vivir, el término límite muchas veces lo asociamos al de frontera, es decir es como cuando llegamos muy cerca a ese algo, tan cerca que pareciera que estamos en ese algo pero sin llegar a él. En la imagen que muestro a continuación se expresa claramente las diversas rectas secantes que se trazan a medida que el punto Q (arbitrario) se acerca o se aproxima al punto conocido P (punto tangencial a la función).

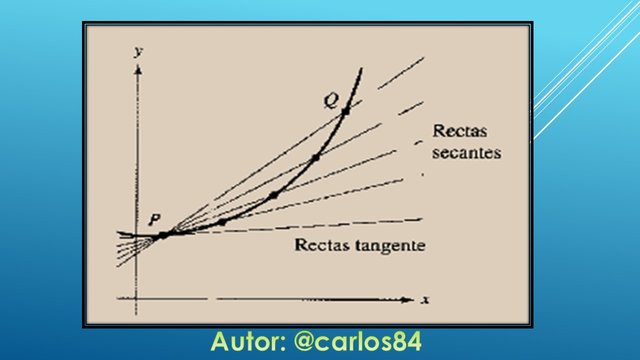
Es así como finalmente para poder calcular la pendiente de la recta tangente conociendo un solo punto, se tiene que recurrir al concepto de límite, con lo que podemos decir que lo que se conoce hoy en día de límite llega gracias al problema que se tenía para calcular la pendiente de la recta tangente conocido solo un punto.

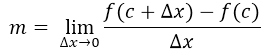
Definición de límite por medio de métodos gráficos y numéricos

Es propicio que para esta parte entendemos lo que es límite de una manera intuitiva, para ello analicemos el siguiente ejemplo:

• Dibujar la gráfica de la función f dada por
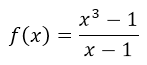
  Antes de graficar es necesario darnos cuenta del dominio de la función, y es que la función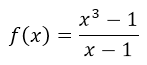 no existe para todos los valores de x, en este caso en particular se puede realizar el gráfico para cualquier valor de x excepto para x=1, ya que para x=1 el denominador de la fracción daría igual a cero, como se sabe dentro de la matemática la división entre cero no está definida.

He aquí otro problema como el de la recta tangente que viene a solucionar el concepto de límite, y es que para valores cercanos a cero pero que no sean cero, puede que existan imágenes reales de la función. Para obtener una idea del comportamiento de la gráfica de f cerca de x=1, se pueden usar dos conjuntos de valores de x, uno que se aproxime a 1 por la izquierda y otro que lo haga por la derecha.

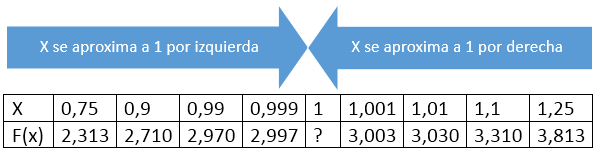
Como podemos ver en la tabla f(x)=3 tanto por izquierda como por derecha.

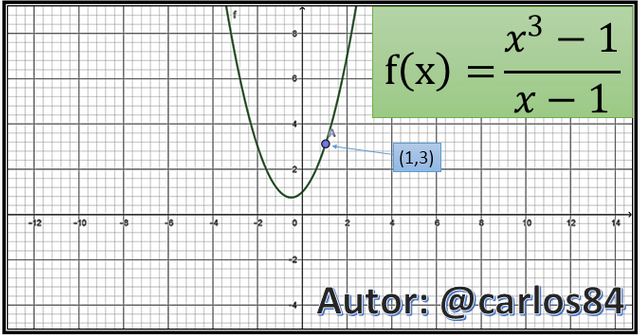
Como se muestra en la gráfica elaborada con el software geogebra 5.0, la gráfica de f representa una parábola con un hueco o discontinuidad en el punto de coordenadas (1,3). A pesar de que x no puede ser igual a 1 y consecuentemente f(x) se acerca a 3 de la misma manera. En conclusión a primera vista pareciera que cuando x toma el valor de uno, la función no existe, pero realmente cuando a x le damos valores cercanos a uno nos damos cuenta que la imagen 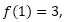y que utilizando la notación que se emplea con los límites, se puede escribir que:

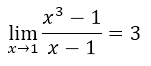
Conclusiones

1. La teoría de límite se origina a raíz de la necesidad de solucionar muchos problemas matemáticos de la antigüedad, como el de calcular la pendiente de la recta que es tangente a un punto de una función cualquiera, el problema de calcular el área que se encuentra por debajo de la curva de una función real también significó un problema que fue arreglado con el descubrimiento de límite.

2. Es de suma importancia manejar el concepto de imagen de una función real, para de esta manera poder comprender lo que significa la teoría de límite desde un punto de vista intuitivo.

3. La teoría de límite es el elemento exacto para delimitar los antecedentes del cálculo infinitesimal y lo que es la ventana abierta para el estudio del mismo.

4. Serán abordados una serie de metodologías de aplicación, teoremas y resolución de ejercicios de límite para el próximo post, donde también se evidenciará la importancia del estudio y aplicación de los límites para evaluar la continuidad de funciones polinómicas.

Referencias consultadas

• Cálculo con Geometría analítica. Autor: Ron Larson y Robert P. Hostetler. 8va edición. Editorial Mc Graw Hill. Volumen I. México 2006.

• El Cálculo. Autor: Louis Leithold. 7ma edición. Editorial Oxford. México 1998.

---

"Para toda aquella persona que le apasiona la matemática, física, química, biología, educación e ingeniería, le recomiendo la etiqueta de #stem-spanol, es una comunidad que valora el contenido intelectual y académico de calidad, conservando siempre la originalidad de las publicaciones, por lo que se recomienda a todos aquellos amigos de steemit que deseen publicar utilizando esta etiqueta a no cometer plagio."