“Los puentes de Königsberg. Nacimiento de la teoría de grafos.”
Hola amigos, deseándoles una muy hermosa tarde, esta vez quiero que conozcan un poco sobre el origen de una de las teorías más destacadas en matemáticas, la teoría de grafos.
En el siglo XVIII la ciudad de Königsberg (Prusia), estaba situada a ambos lados del río Pregel o Pregolya. Este río atravesaba la ciudad, dividiendo la misma en cuatro regiones, para no perder la comunicación, ésta estaba llena de un sistema de puentes conectores. Habían siete puentes: el puente del herrero, el puente conector, el puente verde, el puente del mercado, el puente de madera, el puente alto y el puente de la miel.
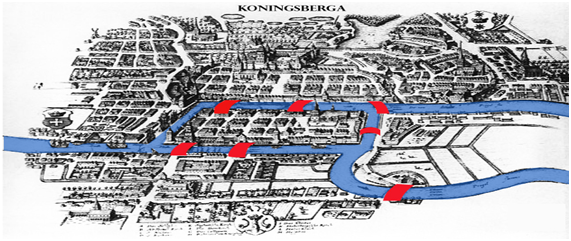
Esta ciudad que en la actualidad pertenece a Rusia, y es llamada Kalinindrado, fue protagonista de un juego cuyo origen se debe a la disposición de los puentes que la atravesaban, y a la curiosidad de los lugareños que pretendían atravesar la ciudad por ellos en sus tardes de paseo.
¿Es posible recorrer cada una de las regiones de esta ciudad pasando por los siete puentes, atravesando sólo una vez cada puente y regresando al mismo punto de donde se partió?
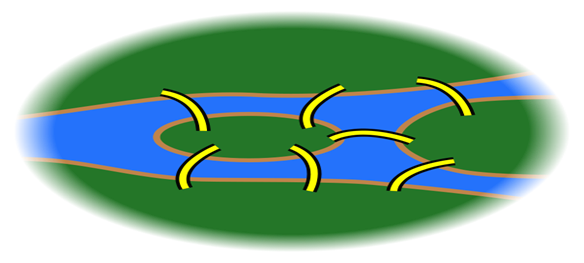
Poco a poco este enigma fue tomando fama, hasta despertar el interés de algunos matemáticos y en especial el de Leonhard Euler, matemático Suizo, quien se encontraba en San Petersburgo (Rusia), cuando escucho de dicho problema.
Para resolverlo Euler simplifico la situación, mediante la sustitución de las regiones de tierra por puntos, y los puentes por trazos (líneas), generando un esquema simplificado representado en la siguiente figura.
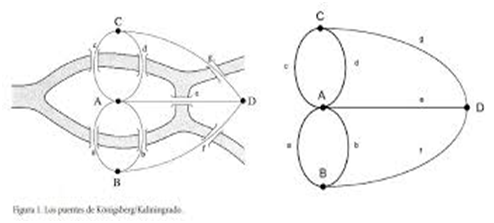
De esta manera, la isla está representada por el punto “A” al cual llegan cinco trazos, que son los cinco puentes que dan con ella. La figura resultante es un grafo ( Un conjunto de puntos llamados "vértices o nodos" del grafo y un conjunto de líneas que los unen, llamadas "aristas o lados" del grafo).
El problema se reduce entonces en dibujar la figura, partiendo de un punto, siguiendo un trazo, sin levantar el lápiz del papel y sin recorrer una misma línea dos veces. A un tal recorrido se le llama camino Euleriano en teoría de grafos.
Para poder recorrer un sistema de este tipo, Euler demuestra que es necesario que los vértices “intermedios”, tengan una vía para entrar y una vía para salir, es decir, deben tener un número par de aristas, y sólo los puntos de inicio y salida pueden tener un número impar de aristas. En otras palabras, Euler demuestra lo siguiente:
Si existe un camino Euleriano, se nos presentan dos posibilidades:
1. El punto de partida y de llegada es el mismo, entonces en todos los vértices concurre un número par de aristas.
2. Los puntos de partida y de llegada son distintos, entonces hay dos vértices con número impar de aristas (el de partida y el de llegada) y todos los demás tienen un número par de aristas.
El recíproco de esta afirmación es también cierto, es decir, si ocurre alguna de las dos posibilidades anteriores, existe un camino Euleriano y podríamos realizar la figura correspondiente sin levantar el lápiz del papel y sin pasar dos veces por una misma arista. Además, si todos los nodos tienen un número par de arista se puede empezar por cualquiera de ellos y se terminará, naturalmente, en el que se empezó; y si hay sólo dos con un número impar de aristas, se empieza en uno de ellos y se termina en el otro.
Notemos que uno de los requisitos en el problema de los puentes de Königsberg es que el punto inicial debe ser igual al punto final, por lo que no podría existir ningún vértice conectado con un número impar de líneas. Pero este no es el caso de este grafo particular, pues en cada vértice concurren un número impar de aristas, por lo tanto, en él no puede ser un camino Euleriano, es decir ¡No es posible planificar un paseo que recorra todos los puentes una única vez!
La investigación que realizó Euler para este problema fue presentada en 1736 en la Academia de Ciencias de San Pesterbusgo. Obra que se considera como el origen de la Teoría de Grafos, y que forma parte de la Topología, rama de las Matemáticas que Leibniz llamó "Geometría de la posición". Teoría que también fue usada por primera vez en ingeniería por Gustav Kirchhoff en 1847, para el análisis de redes eléctricas, formulando leyes de circuitos para calcular el voltaje y la corriente en los circuitos eléctricos, conocidas como leyes de Kirchhoff. Además la teoría de grafos actualmente es aplicada en ciencias sociales, ingeniería, resuelve problemas de estrategias de juegos, de cálculo de rutas óptimas, ciencias de la computación como la inteligencia artificial, la robótica, la genética, teoría de cambio y lógica de diseño o el diseño de redes.
Pues bien amigos, la próxima vez que les reten a repasar cierta figura sin levantar el lápiz, ni repetir un trazo, solo debes fijarte en la paridad de aristas que sus vértices poseen y así no perderán tiempo haciendo vanos intentos.
Recuerda:
Si la condición del reto es que debes llegar al mismo punto de donde partiste, entonces todos los vértices deben tener asociado un número par de aristas. Si el anterior no es el caso, entonces los vértices (donde partiste y donde llegaste) tienen asociado un número impar de aristas. Si tu grafico cumple lo expuesto, entonces sí, ¡puedes hacerlo, inténtalo!
Veámoslo gráficamente.
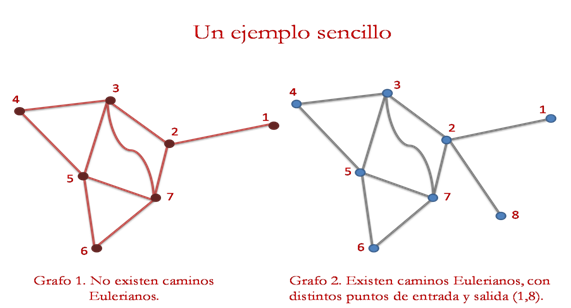
Notar que en el primer grafo no existen caminos Eulerianos, esto se debe a que el vértice 1 posee una sola arista (número impar), y no hay otro vértice con la misma característica, pues todos los demás poseen un numero de aristas par; por tanto no hay forma de realizar un recorrido por cada trazo sin pasar dos veces por la arista que une al vértice 1 con el 2. Sin embargo, en el grafo 2 que se obtiene de agregarle una arista al grafo 1, tenemos solo dos vértices con una arista, aplicando Euler (caso2), si existen caminos Eulerianos en él, es decir, podremos recorrer cada línea del grafo 2 sin repetir ninguna pero no podríamos llegar al punto de partida.
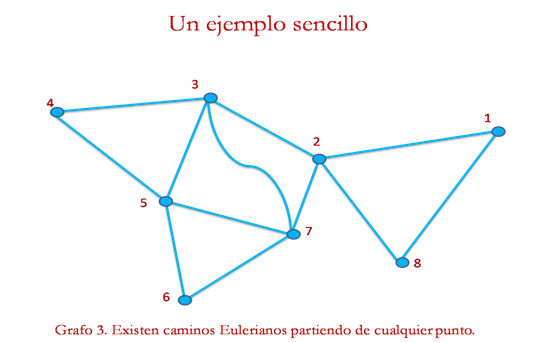
Notar que en el grafo 3 agregamos una nueva arista de tal manera que los vértices 1 y 8 tendrán ahora un numero par de aristas, aplicando Euler (caso1), partiendo de cualquier punto siempre encontraremos caminos Eulerianos en él.
¿Sabías qué?
¡Puedes colorear un mapa cualquiera solo con cuatro colores sin que dos regiones adyacentes posean el mismo color!
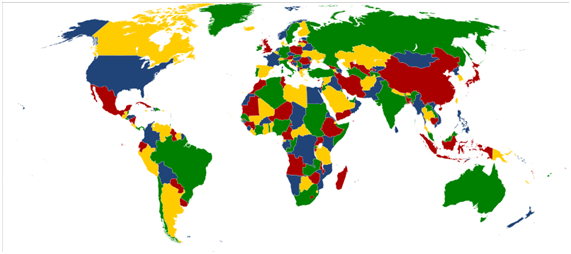
Pues sí, este es un famoso resultado conocido como “Teorema de los cuatro colores”. Dicho teorema fue demostrado por Kenneth Apple y Wolfgang Haken en 1976, un siglo después de que fuera formulado por el matemático Francis Guthrie en 1852. Esta demostración basada en teoría de grafos, se realiza de forma computacional, en donde cada región del mapa es representada por un vértice o nodo, las aristas representan la relación fronteriza entre las regiones, y donde dos regiones “pintadas” con el mismo color no podían estar conectadas entre sí por ninguna arista.
Muy bien amigos lectores, esperando hayan entendido y agradecida de corazón, me despido hasta una próxima entrega .

Congratulations @carolina88! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
¡Felicidades! Esta publicación obtuvo upvote y fue compartido por @la-colmena, un proyecto de Curación Manual para la comunidad hispana de Steemit.
Si quieres saber más sobre nuestro proyecto, acompáñanos en #la-colmena, nuestro canal de Discord dentro de Curation Collective.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por el apoyo, que bueno que mi trabajo les agrade :) claro que los visitare.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Este post fue compartido en el canal hispano #la-colmena de la comunidad de curación Curation Collective y obtuvo upvote y resteem por la cuenta de la comunidad @c-squared después de su curación manual.
This post was shared in the #la-comena channel in the Curation Collective Discord community for curators, and upvoted and resteemed by the @c-squared community account after manual review.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchísimas gracias. Saludos amigos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by carolina88 from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy interesante lo que haces gracias por darle una calida bienvenida a mi novia @astrid.carvajal,un abrazo exitos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por tu tiempo y comentar, un gusto que les agrade :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @carolina88! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit