Podemos decir que una línea recta, el mismo como cualquier curva contenida completamente en un avión es representada, en cuanto a un sistema de ejes Cartesianos, por una función de dos variables, cualquier tiempo la función arriba mencionada es capaz de expresar la condición común que allí satisfacen absolutamente cada uno y cada uno de los puntos que constituyen la línea arriba mencionada. Por ejemplo, si pensamos en una paralela de línea recta al eje de las abscisas, tenemos que comenzar para saber donde la felicidad paralela es planeada, su talón de ecuación es y =mx b. Con la aplicación de Geogebra, nosotros la ecuación de la línea recta para ver su punto del visión mejor, como en este caso en b, que es el término independiente, en aquel m es una constante.
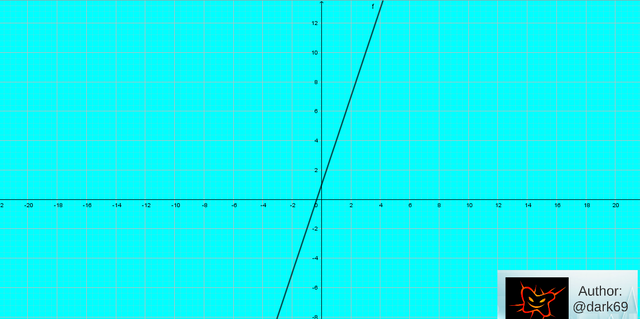
La función de la línea recta charted es la siguiente y=3x 1, donde el m = 3 y b = 1 cuando podemos ver el tribunal en el eje y en 1. (Elaborado por @dark69)
La ecuación de la línea recta que pasa por el origen del sistema de coordinado Cartesiano.
vamos ahora a demostrar que completamente, directamente que pasa, para el origen del sistema de coordenadas ello es representado por una función de la forma y=mx o una función de dos variables del primer grado, sin el término independiente, en aquel m es una constante qué sentido estableceremos más tarde. Para este, tenemos que hacer, para ver que esta función establece o expresa la condición común a la cual allí encajan absolutamente todos los puntos, que constituyen una línea recta que pasa para el origen, en otras palabras debemos indicar que la ordenada y de cualquier punto de la línea recta realmente m es igual al producto de constante para la abscisa x del punto arriba mencionado, o sea y=mx.
Usando la aplicación de Geogebra, nosotros carta nuestra ecuación y=mx.
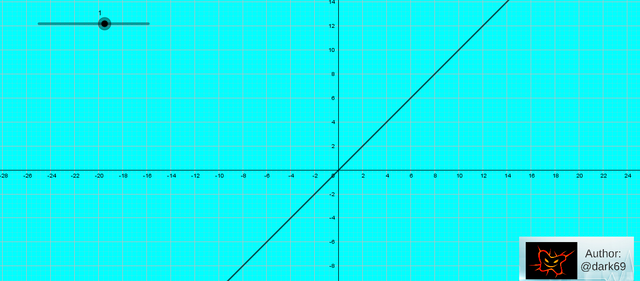
el análisis de nuestra ecuación amantes de las matemáticas tenemos, comenzaremos para hacer x=0 en la función, resultando parecer a esto y=0; Está aquí allí tiene un punto O (0,0) que coincide con el origen de las coordenadas. Inmediatamente damos a la variable x otro valor, por ejemplo c, demostrando y=mc. (Elaborado por @dark69)
Dependiente en línea recta (m).
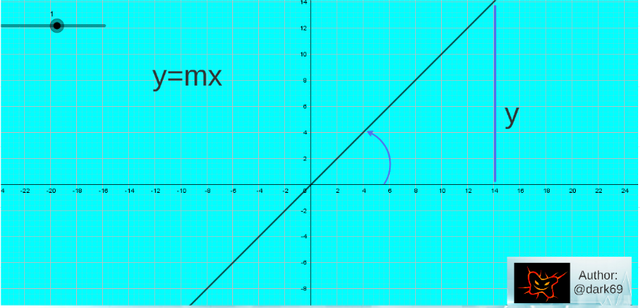
lo abordamos de la siguiente manera, con la intención de ver el sentido del m constante aludiremos a la línea recta y=mx, que supondremos que esto forma un ángulo un positivamente, en cuanto al sentido positivo del eje de x.
En la línea recta tomamos un cualquier punto
P (x, y), de que planeamos el perpendicular un al eje de x, los y se afilian al punto del origen con el cualquier punto P, formar el rectángulo de triángulo, obteniendo la función trigonométrica siguiente: x y tan un =; pero de la función dada apropiada y = m x, es deducido que x y m = Substitución en la igualdad anterior, es tenido: tan un = m.
El m constante es la tangente el trigonométrico del ángulo de inclinación de la línea recta que exactamente recibe el nombre de pendiente de la línea recta, ya que esto controla la inclinación más grande o menor en cuanto al eje de x. Tomando en la cuenta que el m colgante depende de un ángulo y que esto es un coeficiente de x en la función y=mx, también puede ser llamado un coeficiente angular de la línea recta.
Cuando el m constante es positivo, esto indica que el ángulo un de la inclinación de la línea recta es agudo y, cuando es negativo, que el ángulo arriba mencionado mide más de 90 °, pero sin venir a 180 ° para exceder este valor.
Es importante saber que, la Geometría Analítica es conveniente en parámetros que llaman de una línea, línea recta o curva, a las constantes que intervienen en la función correspondiente representativa y de cuyos valores numéricos allí depende la posición que tiene la línea , este independientemente del nombre propio y GEOMETRÍA ANALÍTICA, el sentido de cada constante. Consecuentemente, los parámetros de la línea recta cuelgan el m y arreglaron el origen b, porque ellas son estas dos constantes de las cuales la posición exacta de la línea recta depende.
Sabemos perfectamente que la expresión y=mx b es una función de dos variables, pero uno tolera para llamarlo una ecuación de la línea recta, porque del punto de vista gráfico su solución es sólo una línea recta.
Elaborado por @dark69.
Para concluir que tenemos, de que esta ecuación es usada como un instrumento matemático, en el campo de la ciencia de otros como la Física, para el estudio del movimiento, en la Astrología, planear ellos distancian en el punto en una línea recta entre las estrellas, en la tecnología, este instrumento es aplicado en el Gps para marcar distancias, y en los radares aplicados en el sistema de navegación.
bibliografía de Segunda mano.
Geometría analítica y Trigonometría - la Página 248 para Elena de Oteyza de Oteyza, Emma Lam Osnaya, Carlos Hernández Garciadiego – 2001.
Cálculo diferencial e Integral - la Página 21 – 2007.
Geometría analítica - la Página 80 para René Jiménez – 2006.
