Resolución de SEL por el Método de Gauss en Matlab

Resolver un Sistema de Ecuaciones Lineales (SEL) puede consistir en un proceso de Igualación, Sustitución o Eliminación. Sin embargo, pueden expandirse los métodos para resolverlo si se construyen matrices equivalentes.

Siendo A la matriz de coeficientes, b el vector de términos independientes y x el vector solución, se puede emplear el Método de Gauss para hallar los valores de x.

A continuación, les presentaré cómo programar dicho método en Matlab R2015a, para que puedan determinar el valor de sus variables rápidamente, incluso para un SEL muy grande. Hay que resaltar que, sin embargo, este método genera resultados correctos si y solo si la condición de A es menor que 100.

El pseudo-código del programa, obtenido de la Guía de Prácticas de Laboratorio de los profesores Mirleth Rodríguez y Douglas Pérez, es el siguiente:

Primero, inicien Matlab y creen una función. Colóquenle un nombre conveniente para recordar que es el Método de Gauss. Sus argumentos de entradas serán la matriz A y el vector columna b, mientras que el resultado será el vector columna x.

Luego, se estudiarán las dimensiones de A y b, siendo m y o el número de filas y n y p el número de columnas, respectivamente para la matriz y el vector.

Ahora se puede verificar que los datos ingresados son válidos para hacer el cálculo, pues se sabe que para que un SEL tenga solución única, debe cumplir con ciertas condiciones. Suponiendo que no se cometieron errores ingresando únicamente valores numéricos para A y b, estas condiciones, para la lectura de Matlab, deben ser que A sea cuadrada, es decir, que m=n; que el número de columnas de A sea igual al número de filas del vector b, es decir, n=o; que b sea un vector columna, es decir, p=1; y, por último, que la condición de A sea menor que 100, es decir, cond(A)<100. Si alguna de estas condiciones no se cumple, se puede arrojar un mensaje de error.

Si cumple con todas estas condiciones (o no cumple con las condiciones contrarias, como se muestra en la captura del programa), entonces se puede pasar a crear la matriz expandida M a partir de A y b.

Como es sabido por cursos de matemática o álgebra lineal, el Método de Gauss reemplaza una ecuación por otra equivalente a partir de una segunda ecuación del mismo SEL, y, a su vez, anula los demás coeficientes de una columna en particular. Para esto, de esta segunda ecuación se toma un “pivote”, que es el principal factor para la sustitución. Para evitar errores de redondeo, al programar el Método de Gauss en Matlab, el pivote debe ser el término cuyo valor absoluto sea más grande entre los demás términos en la columna analizada. Así, se debe analizar qué término será el pivote para colocar su correspondiente ecuación (fila de coeficientes de M) en la posición adecuada. Por matemáticas, el pivote no puede ser igual a cero, ya que quisiera decir que los demás términos de la columna son cero (recuerden que se estudió una columna completa para tomar el término con mayor valor absoluto), y esto no generaría una solución única del SEL.

Ahora que la fila del pivote está en una posición conveniente (por encima de los términos que se quieren modificar), se procede a sustituir cada una de las filas inferiores con base en la fila del pivote.

Como se puede ver, este procedimiento se hizo con un ciclo for, por lo que se aplicará a toda la matriz M.

Luego de esto, se crea un vector columna nulo x, y su último término es reemplazado por el cociente entre los dos últimos términos de M, ya que correspondería a x=A/b para la única variable que tiene coeficiente no nulo de la última fila.

Por último, se realiza la llamada Sustitución Inversa, que consiste en reemplazar el valor de las variables ya calculadas en las ecuaciones donde aún falta calcular una variable, para así despejarla y obtener su valor.

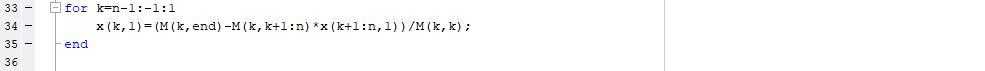
Si no solo se desea guardar el vector solución x sino que también se desea visualizarlo, solo se debe escribir una línea adicional.

A continuación, les dejo una captura del programa completo para una mejor visualización.

Bibliografía