Saludos estimados steemians

El día de hoy saco un poco de tiempo para seguir compartiendo con ustedes temas relacionados con los matemáticas, en especifico lo básico de esta disciplina. En esta oportunidad hablaremos sobre los determinantes, una técnica algebraica relacionada con las soluciones a sistemas de ecuaciones lineales y de primer grado, algo super básico que forman parte de las lecciones de matemática en la secundaria y ademas de fácil compresión, entonces consideremos el siguiente sistema:

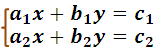
Recordemos que generalmente la solución a este sistema puede obtenerse por medio de los métodos de sustitución, eliminación, igualación o cualquier tipo de artificio matemático de manera que podemos obtener:

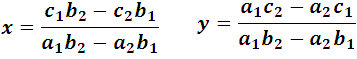
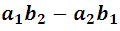
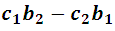
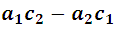
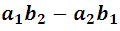
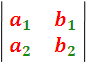
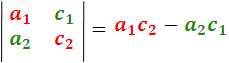
Notemos que el denominador es común para ambas variables y es obvio que debe ser diferente de 0. Ahora bien, las diferencias entre los productos: , y que aparecen en las soluciones, la podemos obtener con facilidad, si adoptamos un símbolo especial, y establecemos que :

se representa por el símbolo al cual se le denomina

, por estar formado por cuatro elementos y dispuestos en dos filas y en dos columnas. Los elementos a₁ y b₂ se dice que forman la diagonal principal del determinante y representa el primer producto, luego los otros dos elementos complementa la expresión En resumen, según lo establecido resulta, pues, que:

Y esta diferencia expresa el valor o desarrollo del determinante. De manera similar:

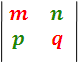
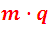
Forman otros dos determinantes de 2⁰ orden. De una manera general, el símbolo , representa la diferencia entre los productos y , es decir, sus diagonales.

Propiedades de los determinantes de segundo orden.

En los determinantes de segundo orden podemos notar, entre otras, las siguientes propiedades:

• El valor de un determinante de segundo orden no altera si combinan las filas por las columnas. Así que:

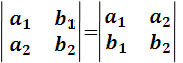
pues ambos son iguales a .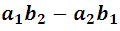

• Permutando entre sí las dos filas o las dos columnas, el determinante cambia de signo, pero no de valor absoluto.

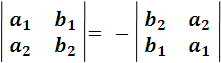
en efecto:

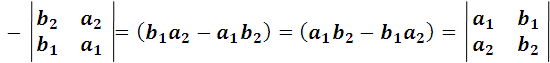
• Si las dos filas o las dos columnas son idénticas, el determinante es nulo.

Así:

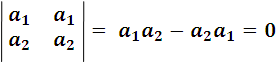
Resolución de sistemas de ecuaciones por determinantes

Como ya lo mencionamos los determinantes de segundo orden podemos aplicarlos en la resolución de un sistema de dos ecuaciones lineales con dos incógnitas. En efecto, en la forma general de estos sistemas encontramos que:

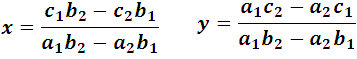
Valores que con los determinantes muy bien lo podemos expresar de la siguiente forma:

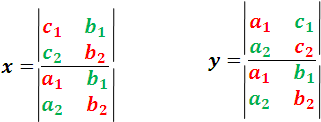
siendo el denominador común diferente de cero, estas ultimas expresiones son también conocidas con el nombre de fórmulas de Crámer (Gabriel Crámer, matematico de Ginebra, 1704-1752). Dichas fórmulas son fáciles de aplicar si se tiene en cuenta que ambas fracciones tienen el mismo denominador, el cual es un determinante formado por los coeficientes de las incógnitas dispuestas previamente en su orden natural; y el determinante del numerador de cada una de dichas fracciones resulta de reemplazar en el determinante común del denominador la columna de los coeficientes de la incógnita que se quiere calcular por la de los términos independientes.

Por ejemplo intentemos resolver el siguiente sistema:

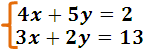
Aplicando lo expuesto, resulta:

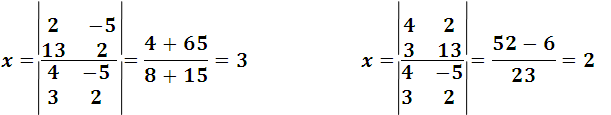
Sin duda alguna que es mucho mas practico resolver estos problemas por medio de los determinantes, y son de mayor utilidad a la hora de resolver de sistemas de ecuaciones de tercer orden, como lo mostraremos a continuación

Determinantes de tercer orden

Consideremos el siguiente el sistema:

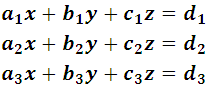
Intentar resolver este sistema por los métodos algebraicos de igualación o sustitución requiere en ellos de muchos pasos algebraicos, por ello es viable utilizar los determinantes y ver como es el desarrollo. El determinante que figura como denominador común se representa por la notación:

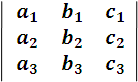
y de manera análoga podemos representar los otros determinantes que aparecen en los numeradores. Procediendo de esta manera la solución del sistema la podemos expresar así:

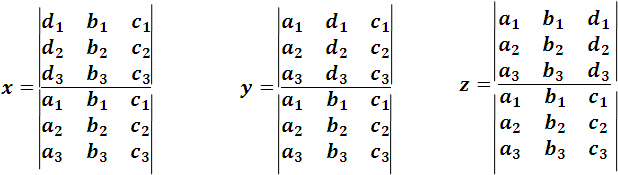
Podemos notar que de igual manera que en un sistema de dos ecuaciones con dos incógnitas, en ele denominador común aparece el determinante formados con los coeficientes de las incógnitas dispuestas previamente en su orden natural, y los determinantes que figuran en los numeradores se forman sustituyendo la columna de los coeficientes de la incógnita que se calcula por la columna de los términos independientes.

Para obtener el desarrollo, podemos acudir al siguiente diagrama, en el cual, para mejor comprensión, marcamos con puntos los lugares ocupados por los distintos elementos del determinante señalado:

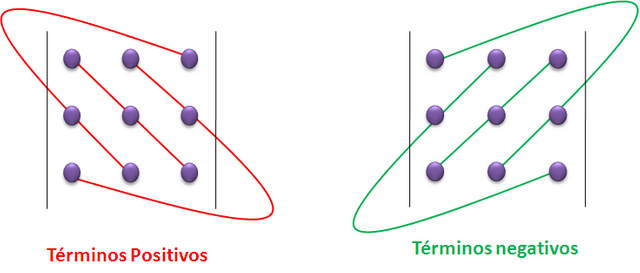
Se puede observar que la diagonal principal y sus paralelas, cada una de estas ultimas con el elemento del vértice opuesto, forman los términos positivos, y la otra diagonal y sus paralelas, cada una de estas ultimas con el elemento del vértice opuesto respectivo, los términos negativos. Esta regla para expresar las soluciones de los sistemas lineales se le llama regla de Crámer, en resumen, el determinante de tercer orden es toda expresión de la forma:

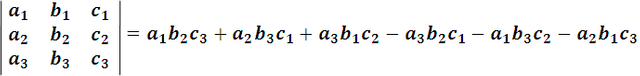
Para ver un ejemplo resolvamos el siguiente sistema:

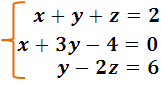
Comenzamos por ordenar el sistema en su forma natural y resulta:

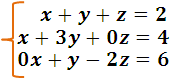
Aplicamos ahora la regla de Crámer se tiene:

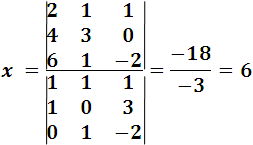
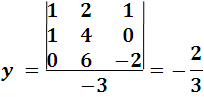
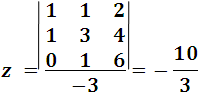
De esta manera queda demostrado lo fácil, practico y útil de los determinantes para solucionar problemas con respecto a sistemas de ecuaciones lineales de primer orden. Mas adelante estaré compartiendo otros puntos respecto a los determinantes y las generalidades sobre matrices.

Para mayor información con respecto al tema puede consultar las siguientes referencias:

• 1
• 2
• 3
• 4

Hasta la próxima steemians

by @juancmz