Soy estudiante de ingeniería electrónica de la Universidad Simón Bolívar de Venezuela (USB), hace unos trimestres me encontraba cursando la materia “Circuitos Digitales” donde se nos estuvo evaluando el diseño de circuitos lógicos a través de distintos simuladores entre ellos el simulador “Logisim”. Una de nuestras primeras evaluaciones fue el simplificar expresiones lógicas obtenidas mediante tablas de la verdad y simular un circuito combinatorio de cuatro entradas y dos salidas. Por especificaciones del profesor se utilizo la suma reducida de los dos últimos números del carnet universitario de cada estudiante para realizar una serie de actividades.
Actividad 1:
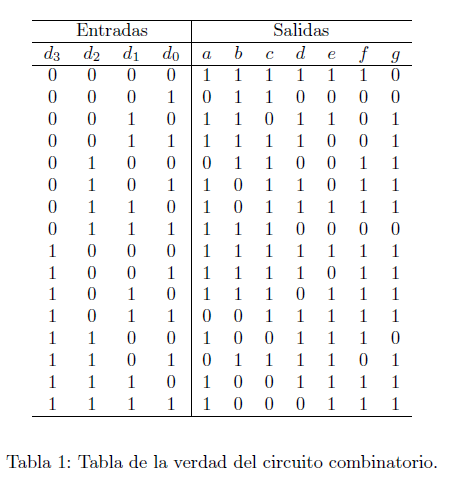
Una compañía desea hacer la ingeniera inversa de un circuito combinatorio desarrollado por la competencia. Dicho circuito lógico posee 4 entradas y 7 salidas. Uno de los ingenieros de la compañía logró obtener la tabla de la verdad del circuito. La relación de entradas-salidas se muestra en la “tabla 1”. En esta actividad, se requiere que su grupo obtenga la expresión de dos de las salidas del circuito lógico usando “minterms”. La distribución de las salidas se realiza según la “tabla 2”.
Actividad 2:
Usando las funciones lógicas obtenidas en la Actividad 1, simplifique dichas ecuaciones usando algebra y propiedades de la lógica booleana.
Actividad 3:
Simplificar las funciones lógicas asignadas usando la técnica de mapas de Karnaugh.
Actividad 4:
Implemente las funciones lógicas obtenidas en la Actividad 1 y Actividad 3 en el simulador “Logisim”, y verifique que los circuitos cumplen con los valores de referencia, es decir, con los valores de la tabla 1.

Diseño y resultados:
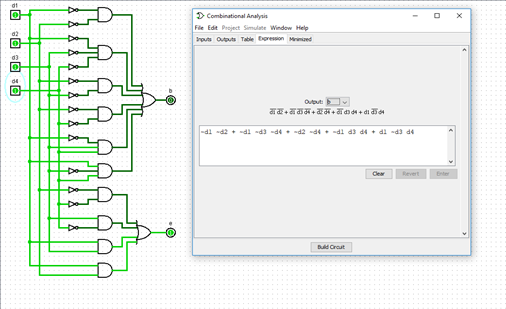
Tras realizar la suma reducida de los dos últimos números del carnet se obtuvo 4 y siguiendo la Tabla 2 (Asignación de las salidas según la suma de los últimos números del carnet.) se procedió a trabajar con las salidas b y e y se realizaron las actividades con los cálculos a mano:

Se utilizó la tabla para construir las funciones lógicas.

Se procedió a realizar la simplificación de las dos expresiones obtenidas y se hallaron simplificaciones para b y e:

Luego se procedió a elaborar los correspondientes mapas de Karnaugh a mano para poder hallar nuevamente la expresión lógica más simplificada:
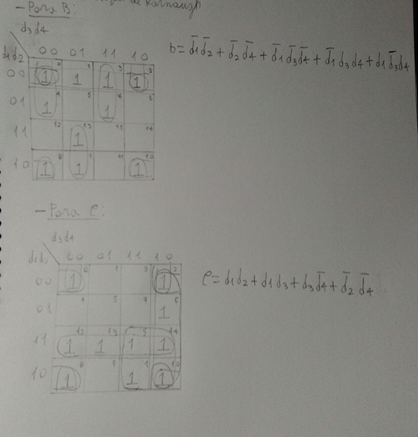
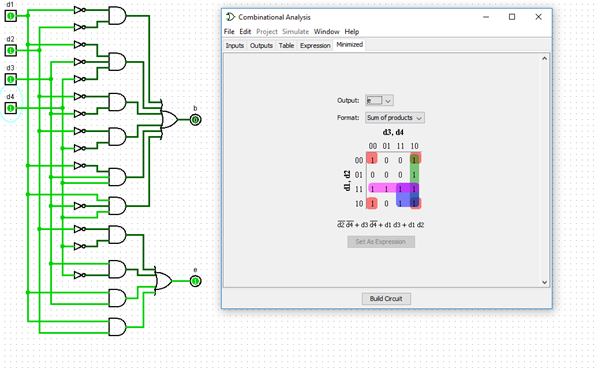
Posteriormente se procedió a las simulaciones en “Logisim” ingresando la tabla de la verdad inicial obteniendo la expresión algebraica más reducida y los mapas de Karnaugh correspondientes a cada salida:
Para b:

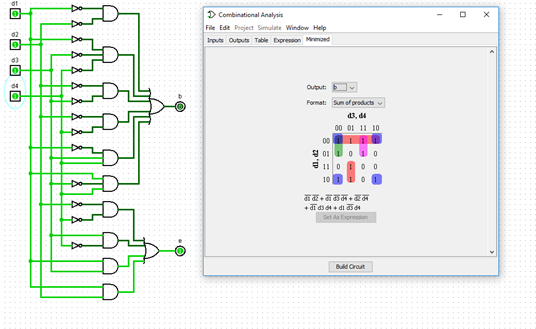
Para e:

Discusión:
Se logró diseñar el circuito combinatorio de cuatro entradas y dos salidas y simularlo en “Logisim”. Al comparar las funciones de cada salida obtenidas mediante el mapa de Karnaugh y mediante el simulador, respectivamente, se evidencia que se obtiene los mismos resultados, pero al compararlas las expresiones obtenidas utilizando minterms se encuentran diferencias ya que estas últimas son más largas. Esto se debe a que la manipulación de lógica booleana debe ser más extensa para lograr llegar a los mismos resultados, lo cual no se logró debido a que las expresiones son más engorrosas. En consecuencia, al utilizar el mapa de Karnaugh y el simulador se logran resultados más exactos, precisos y prácticos, por su puesto el análisis manual sigue siendo válido y se llegaría a los mismos resultados, pero no resulta nada eficiente debido a lo largo y a que es muy fácil equivocarse en estos cálculos.
Referencias:
Harris Sarah y Harris David “Digital design and computer architecture”, editorial “Morgan Kaufann”, 2013.
Angel Terrones, "Actividad 1", entregado el 1/11/18
Buen trabajo. Qué bueno que te animes a compartir aquello que estás estudiando. Al leerte también me pongo a recordar varias cosas en la temática de arquitectura del computador. Te animo a aprender a usar la aplicación de steemstem que es idónea para subir este tipo de contenidos a la blockchain. Recibirás también recompensas adicionales en los votos por usarla. También te invito a unirte al servidor de STEM-Espanol en Discord si no lo has hecho.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hey! Muchas gracias amigo!! Muy interesante la información! Ya lo se para la siguiente oportunidad!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @orbital753! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPTo support your work, I also upvoted your post!
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail. It is elligible for support from @curie.
If you appreciate the work we are doing, then consider supporting our witness stem.witness. Additional witness support to the curie witness would be appreciated as well.
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Please consider setting @steemstem as a beneficiary to your post to get a stronger support.
Please consider using the steemstem.io app to get a stronger support.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit