¡Hola queridos lectores coloridos! El día de hoy les traigo un post que llevaba un tiempo preparando, quise intentar algo diferente y por ello elaboré un informe tipo ensayo, donde expresé mi opinión sobre dos temáticas que amo: las matemáticas y la ilustración.

Si ya leyeron el titulo del post ‘’La importancia de las matemáticas en la ilustración’’ ; tengo Fe de que algún diseñador me este leyendo y sepa entender a que me refiero (jejeje) pero me entusiasma enseñarles como las matemáticas influyen en el desarrollo de cualquier diseño y/o ilustración permitiendo obtener resultados increíble en nuestras creaciones. Sin mas preámbulo, sigan leyendo y entérense de algunos secretos matemáticos dentro del diseño.
El número de oro o EL NÚMERO PHI
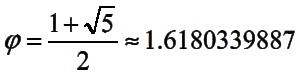
Fuente: Diseñado por mi persona 2018
Phi es un número irracional, φ =1.618033988749895…, que representa la proporción áurea o el llamado número de oro, y que es una razón definida por la siguiente construcción geométrica, con su ecuación asociada:
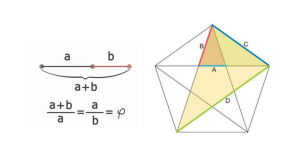
Fuente: http://www.sacred-geometry.es
Además, el estudio y descubrimiento de este fabuloso número que aportó muchísimo en la historia de la arquitectura, la matemática y las ciencias…y en la actualidad lo encontramos, presente en el diseño y la composición. Puedo añadir que el número π se obtiene al dividir la longitud de una circunferencia entre su diámetro. Los habitantes de Egipto y Mesopotamia (hace más de 4000 años) ya utilizaban aproximaciones bastante buenas de nuestro famoso número. En Egipto se utilizó el valor 256/81 ≈ 3,16, y en Mesopotamia 25/8 = 3,125.
Fuente: Número de Oro
El primero en descubrir un método para calcular su valor fue Arquímedes de Siracusa, quien vivió durante el siglo III a. C. Sus avanzados métodos y su gran ingenio le llevaron a concluir que el valor de π era aproximadamente 22/7 ≈ 3,14286. Encontró además las fórmulas para el área del círculo (π·r2) y el volumen de la esfera. (4·π·r3/3)
Según lo que leí en el blog de José Goznes, señala que : A partir del siglo XVII empieza una carrera imparable por calcular π con precisión. En 1615, Van Ceulen calcula 35 cifras decimales, Machin en 1706, 100; Shanks en 1874, 527; Smith y Wrench en 1949, 1120. Las 100,000 cifras se alcanzan en 1961, el millón en 1973, los mil millones en 1989. El 20 de septiembre de 1999, los profesores Kanada y Takahashi de la Universidad de Tokio alcanzan la marca de 206,158,430,000 cifras decimales, tras 83 horas de cálculos con ayuda de un superordenador. Así comienza nuestro insigne amigo.

Fuente: www.masscience.com
WOW
Dato curioso
El número pi es una constante en las matematicas y la naturaleza, que muestra la relación entre la longitud de una circunsferencia y su diámetro. Mira los 100 primeros decimales de Phi:

Fuente: ttps://www.masscience.com
¿Son muchos?, ¿no?. Pues para Tammet, No!. Pues, el matemático británico Daniel Tammet recitó de memoria durante 5 horas y nueve minutos 22.514 decimales de Pi, en el Museo de Historia de la Ciencia de Oxford, un 14 de Marzo, que es el día de Pi; además habla once idiomas, y compara la emoción que se puede sentir ante un número primo con la lectura de versos.
Ahora bien, les contaré sobre la relación fascinante que tiene el número Phi (el número de oro) desde los inicios de la arquitectura, la escultura y el arte…y claro con el diseño en la actualidad.
La Proporción Áurea
De forma simple, la Proporción Áurea establece que lo pequeño es a lo grande como lo grande es al todo. Habitualmente esto se aplica a las proporciones entre segmentos. Esta razón ha sido venerada por toda cultura en este planeta. Podemos encontrarla en el arte, la composición musical, incluso en las proporciones de nuestro propio cuerpo, y en general en toda la Naturaleza "escondida" detrás de la secuencia de Fibonacci.
Entonces si estudiamos el número de oro como un valor medio tenemos que La Proporción Aurea es también una forma de dividir un segmento en dos partes que reproducen la afirmación hecha al inicio: lo pequeño es a lo grande como lo grande es al todo. Considera siguiente segmento:
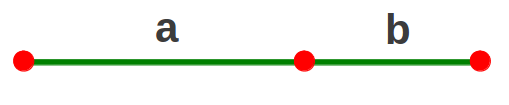
Fuente: http://www.sacred-geometry.es
Esto se puede expresar matemáticamente de una forma sencilla: ab= a+ba. Esta relación puede visualizarse en términos racionales , podría expresarlo como a/b y sigue satisfaciendo la idea principal del valor medio. Tendríamos que Q=a/b, lo cual nos conduce a la misma idea principal:
ab=1+ba⇒Q=1+1Q⇒Q=ab=φ=5+12
De ello deducimos que cada parte (la parte grande A o la parte pequeña B) representan las proporciones siguientes con respecto al segmento total (a+b):
ba+b=11+ab=11+φ=1φ2
aa+b=ab1+ab=φ1+φ=φφ2=1φ
Lo mas interesante de esto es que en el caso especial de un segmento unitario, la sección Áurea proporciona la única forma de dividir la unidad en dos partes que están en progresión geométrica: (tomamos la siguiente imagen como referencia)
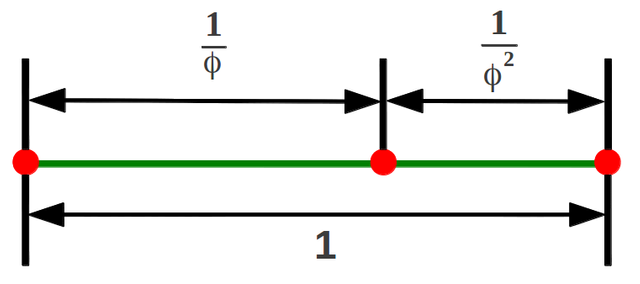
La Proporción Aurea es la única forma de dividir la unidad en dos partes que están en progresión geométrica
Fuente: http://www.sacred-geometry.es
La división de un segmento unitario según la Proporción Áurea es un proceso que puede iterarse de forma indefinida, es decir en muchos segmentos pequeñitos con un valor medio y la primera división proporciona todos los elementos necesarios para hacerlo. La figura siguiente ilustra el proceso de división iterada en Razones Áureas sucesivas. Este proceso también puede iterarse hacia el exterior usando las potencias crecientes de φ
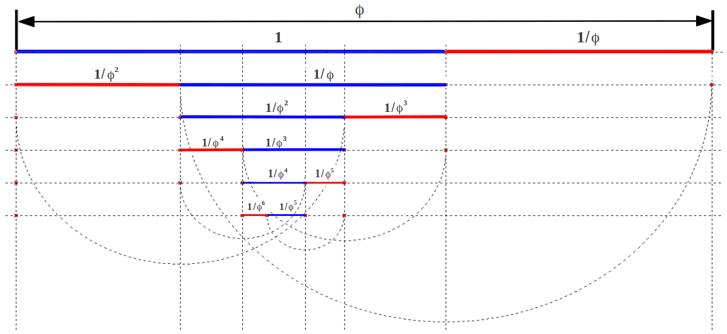
División iterada de un segmento según la Proporción Áurea.
En cuanto a la relación que tiene la Proporción Áurea con la construcción geométrica...
Hay muchas formas de dividir un segmento geométricamente siguiendo la Proporción Áurea. En el primero, tan solo necesitas calcular el punto medio de un segmento dos veces: empezando por el segmento AA, se calcula su punto medio denotado como M. Entonces se marca el punto B de forma que el segmento MB tenga la misma longitud que AA', y se calcula su punto medio . Por último, se marca el punto C tal que M'C=MB y esto es todo. Uno acaba con un segmento AC que está dividió según los Segmentos Áureos AB y BC. Es decir que, ABBC=ACAB=φ
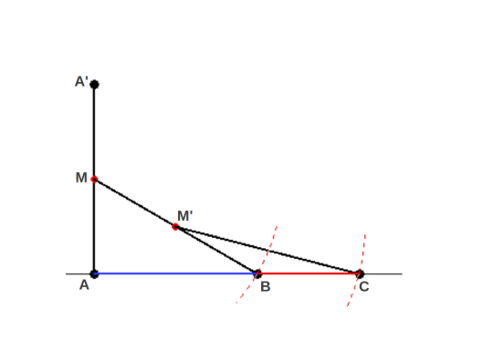
Método 1: Utilizando un compás y escuadras, Construcción geométrica de la Proporción Áurea usando dos puntos medios
Fuente: http://www.sacred-geometry.es
Los otros dos métodos tienen en común el uso de un triángulo rectángulo, con un cateto de longitud doble del otro. En el siguiente método; se empieza por el segmento AC y se calcula su punto medio denotado como M. Entonces se levanta la mitad de ese segmento perpendicularmente a MC para obtener el punto C y el triángulo ACC (cuya diagonal es 5/2). Entonces se lleva la altura del triángulo sobre la hipotenusa AC para obtener el punto B y por último se lleva la longitud AB hacia abajo para obtener el punto B, que divide el segmento original AC según la Proporción Áurea, con lo cual tenemos de nuevo que: ABBC=ACAB=φ
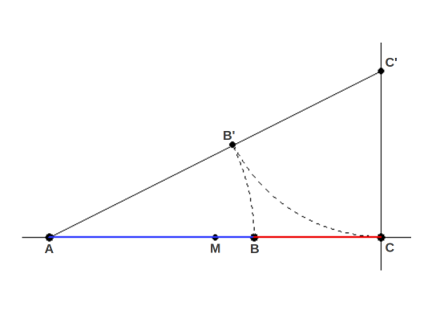
División geométrica de un segmento según la Proporción Áurea usando dos arcos. El segmento original acaba dividido en dos partes Áureas
Fuente: http://www.sacred-geometry.es
El tercer método; empieza por un cuadrado de lado AB . Se calcula el punto medio denotdo nuevamente como M de este lado y se dibuja un círculo con centro en este punto pasando por D hasta que pase por el puno C. Y ya lo tenemos: el segmento AC está dividido según la Proporción Aurea en el punto B, así que tenemos de nuevo la igualdad de ABBC=ACAB=φ
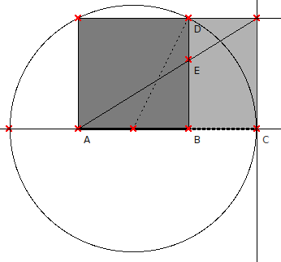
Fuente: http://www.sacred-geometry.es
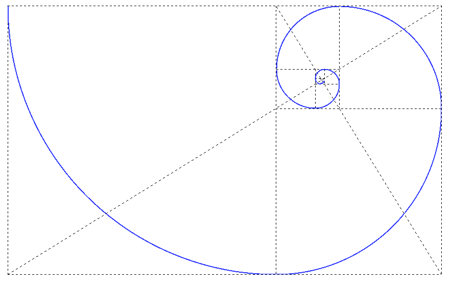
Espiral Áurea
Fuente: http://www.sacred-geometry.es
Importante: A pesar de que los tres métodos geométricos de construir φ son equivalentes, cada uno tiene su uso preferido. Por ejemplo, el método B se usa cuando uno quiere dividir un segmento de longitud conocida en subsegmentos que obedecen la Proporción Áurea. Por el contrario, el método C empieza por un segmento que acabará siendo la parte grande de la división de el segmento total AC en Razón Áurea. El Método A puede usarse cuando no se tiene ningún segmento que dividir pero simplemente se necesita la proporción. Entonces éste se puede trasladar a cualquier segmento deseado por similitud.
Ahora bien, el tercer método los vemos íntimamente relacionado con La sucesión de Fibonacci, entra en el campo de la aritmética y está relacionado con el número de oro. Se trata de una serie infinita de números naturales que empieza con un 0 y un 1, y continúa añadiendo números que son la suma de los dos anteriores, quedando con la siguiente forma de sucesión: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1.597, 2.584, 4.181, 6.765, 10.946, 17.711, 28.657… Uniendo el concepto aritmético/matemático con su representación geométrica se obtiene una de las imágenes más comúnmente asociadas al número y la razón áurea: la espiral de Fibonacci
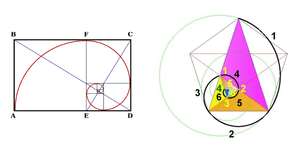
Fuente:http://padresyprofesores.com
Importante : La relación de esta sucesión con el número de oro (PHI) estriba en que al dividir cada número por el anterior de la serie se obtiene una cifra cada vez más cercana a 1,61803, quedando el resultado alternativamente por debajo y por encima del número preciso, sin llegar nunca a alcanzarlo absolutamente.
Entonces, cuando comenzamos a relacionar esta proporción divina en cada uno de los detalles del diseño, la arquitectura, el arte y la fotografía; es importante resaltar que nuestros ojos analizan eficazmente una imagen y la retinen mucho mas, si está encuadrada en un rectángulo áureo, de forma que ésta proporción áurea, se ha utilizado de forma intuitiva desde la Antigüedad hasta nuestros días, porque es la forma más cómoda y agradable a la vista.
¿Sabias qué el famoso logo de mazana de la compañía Apple esta relacionado con la proporción áurea?, ¿Y con la distribución de los pétalos en una flor?, ¿Y con las proporciones de nuestro cuerpo? hasta con el hombre ideal o el Hombre de Vitruvio, dibujado por Leonardo Da Vinci y considerado un ideal de belleza.
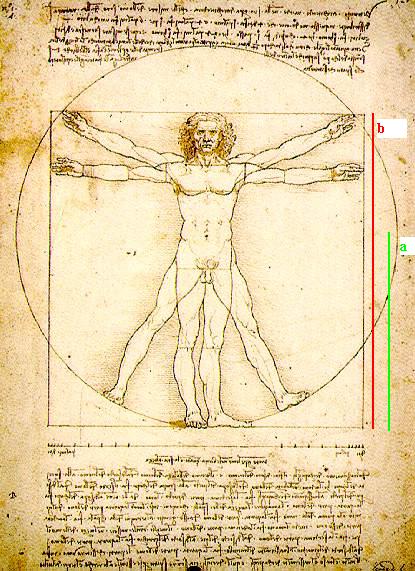
Fuente: Imagen tomada de la página web Razón Áurea
Y pues el diseño del logo de la compañía APPLE diseño su logo de manera ingeniosa y creativa y sin darse cuenta desarrollaron un logo que se adapta a la perfección con la proporción áurea y esto vuelve a confirmar que el nmero de oro es increíble! y logra triunfos en el diseño y la publicidad cuando lo utilizamos correctamente en la composición de diseños.

Fuente: Computer Hoy
Esta proporción ha fascinado desde hace siglos al ser humano, que lo ha considerado un indicador de la perfección y la estética. En el Renacimiento, muchos artistas y arquitectos compusieron sus trabajos con la intención de aproximarse a la proporción áurea, convencidos de que esta relación atribuía a las obras un carácter estético especial.

Fuente: Collage realizado con imágenes tomadas de http://padresyprofesores.com
De una forma u otra, esta ley matemática, así como su historia y su relación con la creatividad humana resulta increíble, fascinante y misteriosa, y su vínculo con el diseño actual de logotipos es sin duda también un tema curioso. Y definitivamente en el ámbito de la publicidad esta comprobado que esta herramienta nos permite construir elementos visualices en el área del diseño que lograr capturar a grandes masas en el mundo
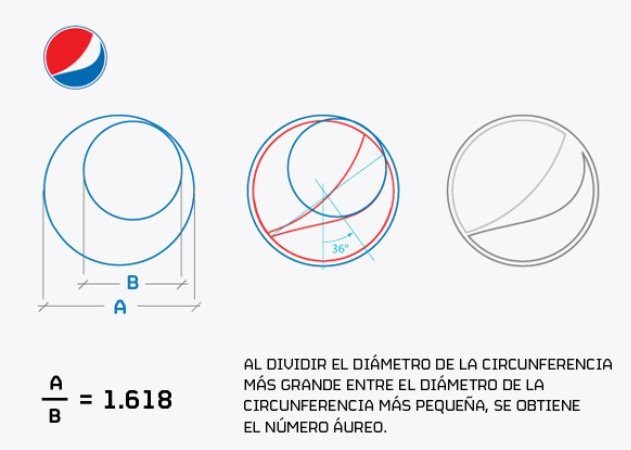
Fuente: Computer Hoy
Además que facilita la construcción de los logros, reduciendo el trabajo y logrando que sea un logo armónico y que se adapte a la tendencia minimalista, debido a que permite reducir los elementos visuales y añade la utilización de lineas y figuras mas definidas que logran adaptarse al concepto gráfico.
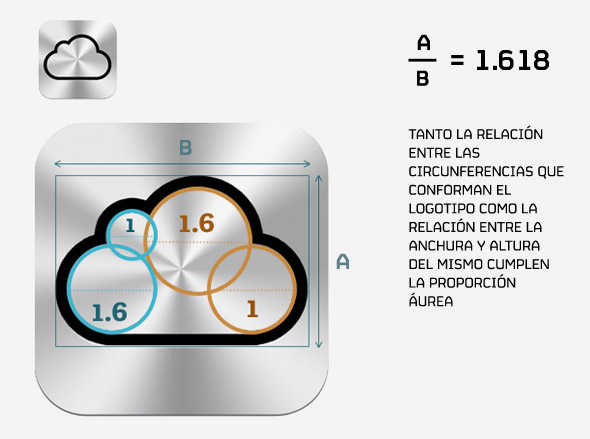
Fuente: Computer Hoy
Para cerrar los invito a animarnos a descubrir en nuestra vida diaria, detalles sorprendentes que nos rodean y se relacionan con el número áureo. Es fantástico y super cool.

Fuente:Nana´s Blog - WordPress.com
Ademas quiero compartir con ustedes con la proporción áurea me ayudó a definir mi marca personal como diseñadora gráfica y logro que mi objetivo de tener un logo maravilloso, armónico se desarrollara adaptándolo correctamente al concepto que tenía.
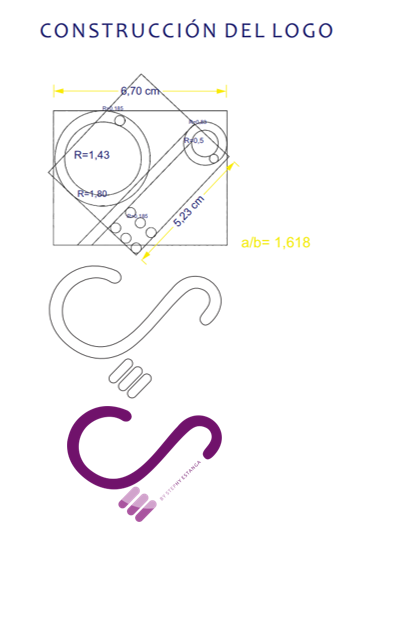
Fuente: Diseño de logo elaborado por mi persona 2017

Referencias:
- Lawlor, Robert: "Sacred Geometry. Philosophy and Practice", Thames and Hudson, 1982, ISBN 0-500-81030-3.
- G.H. Hardy. (1999). Apología de un matemático. Editorial Nivola.
Bueno eso fue todo por el post de día de hoy, espero se motiven a utilizar algún día la proporción áurea; me encantaría saber su opinión sobre mi artículo y la temática, no olviden que hay que aprecias las herramientas de las matemáticas y dejar volar nuestra imaginación para admirar el don de la vida y la perfección de la naturaleza!

FOLLOW ME @STEPHYESTANGA
Por cierto, recuerda que todos los gifs que utilizo en mi blog son de www.giphy.com :')
Sencillamente encantador tu post y super original. Felicitaciones
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola @stephyestanga. Interesante, bonito y entretenido. Su post ha sido votado por @ramonycajal. Cuenta curadora de ciencias de @cervantes.
Un saludo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente @stephyestanga
Como siempre mostrandonos perspectivas diferentes de diversos temas, de una manera sumamente creativa, al estilo stephy. Esta vez, la vinculación de la ciencia con las artes. El aplauso...para tí. Te deseo mucho éxitos. Felicitaciones !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
¡Wao @stephyestanga! Extraordinario post. Eres muy brillante, y por tu esmero en este post tienes bien merecido el voto de @cervantes y más. ¡Felicitaciones y que continuen los éxitos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit