CONOCIENDO EL SOFTWARE LIBRE GEOGEBRA 6
Fuente: Elaborado por @xeliram editadas con el programa Microsoft Power Point en formato jpg.
Cabe destacar que según Pérez (2007) los software de Matemáticas se clasifica en dos categorías, los Sistemas de Álgebra Computacional (CAS, en inglés), que permiten cálculos simbólicos y numéricos, y también representaciones simbólicas (Derive, Mapple, Mathematica y MathLab, entre otros); y los Sistemas de Geometría Dinámica (DGS), estos programas de ordenador permiten la introducción directa en la ventana gráfica de objetos geométricos y la representación dinámica de los mismos (Cabri, Cinderella, entre otros).
En este contexto, Preiner (2008) señala que el Geogebra tiene las dos categorías, el Sistema de Geometría Dinámica (DGS) con ciertas características de un sistema de Álgebra Computacional (CAS). Combina las representaciones gráficas y simbólicas ofreciendo ambas al mismo tiempo. De allí que el Geogebra puede realizar construcciones tanto con puntos, vectores, segmentos, rectas, secciones cónicas, como con funciones que después pueden modificarse dinámicamente.
Para la instalación del Geogebra puedes revisar el artículo: Instalar Geogebra y primeros pasos: Herramienta útil para aprender y enseñar álgebra, geometría y cálculo: de @skatitauriazul, Una vez descargada la aplicación y activada, es importante conocer su interfaz, entre ellos veamos los elementos que presenta la pantalla del Geogebra, donde puedes observar la vista algebraica, vista gráfica, la barra de herramientas y teclado virtual (ver figura 1).
Pantalla del Geogebra
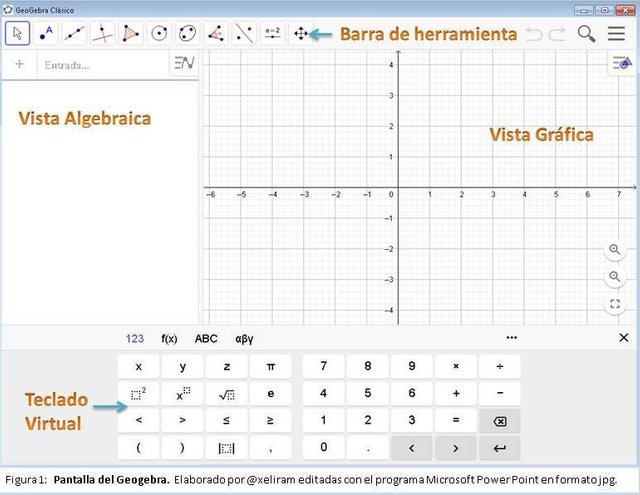
El Geogebra además de la vista algebraica y gráfica ofrece otras vistas: vista gráfica 3D, vista CAS y hoja de cálculo. Cada vista presenta su propia barra de herramientas, excepto la algebraica.
Con un repertorio de herramientas y comandos, así como operadores y funciones que permiten crear construcciones dinámicas con diferentes representaciones de los objetos matemáticos.
Fuente de información:
Vista Algebraica
La vista algebraica se abre junto a la vista gráfica, allí encontraras integrada una línea de entrada donde pueden ingresar directamente expresiones algebraicas, empleando el teclado. Allí se verán reflejadas todas las formulas y objetos de nuestras construcciones. Además observaras la barra de herramientas gráficas, con los botones deshace y rehace (ver figura 2).
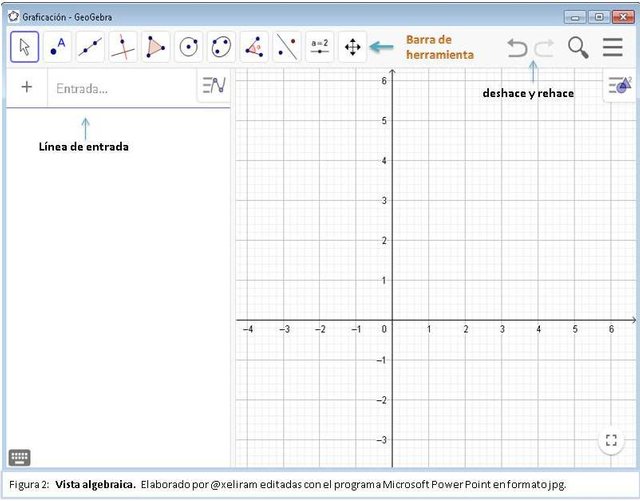
Vista Gráfica
Donde se dibujaran todos nuestros gráficos, esta encabezada por la barra de herramienta gráfica y los botones deshace y rehace. Para realizar construcciones y crear objetos matemáticos se emplea la barra de herramientas, el cual se opera con el raton. Estos objetos creados en la vista gráfica tiene su correspondiente representacion en la vista algebraica (ver figura 3).
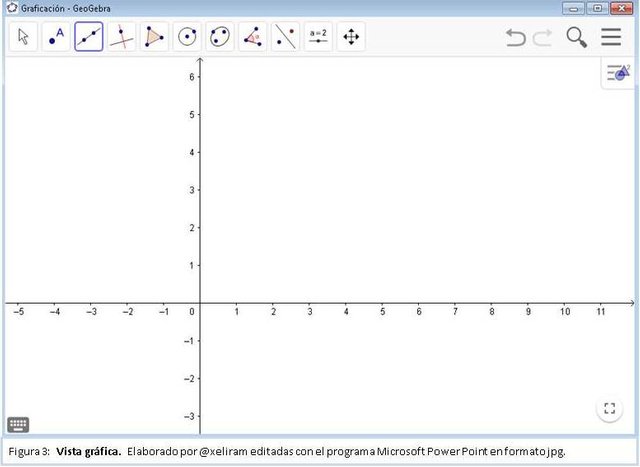
Barra de herramienta gráfica.

Permiten crear objetos geométricos de manera cómoda. Compuesta por once (11) botones muy descriptivos. Según Galaz (sf) Cada uno de ellos permite seleccionar una opción de un conjunto de acciones que, al activarse permiten realizar una operación específica para efectuar la construcción y acción que se desee, estos botones van cambiando según la última opción elegida. Al hacer clic en cada botón, se obtiene un menú desplegable con diferentes posibilidades. Cuando se selecciona una de ellas, aparece un breve texto que explica de manera precisa como usar la herramienta seleccionada.
Vista Gráfica 3D
Se abre por omisión junto a la vista algebraica, en el cual aparece la barra de herramienta de la vista gráfica 3D ubicada en la parte superior de la ventana de Geogebra. Las construcciones creadas en la vista 3D, también se representan en forma algebraica en la vista algebraica, en el cual además de representar objetos como rectas, segmentos, polígonos, cónicas entre otras se pueden representar planos, esferas, conos, poliedros, funciones de dos variables. Para crear objetos se pueden utilizar la barra de herramientas gráfica 3D o ingresar su representación algebraica en la línea de entrada (ver figura 4).
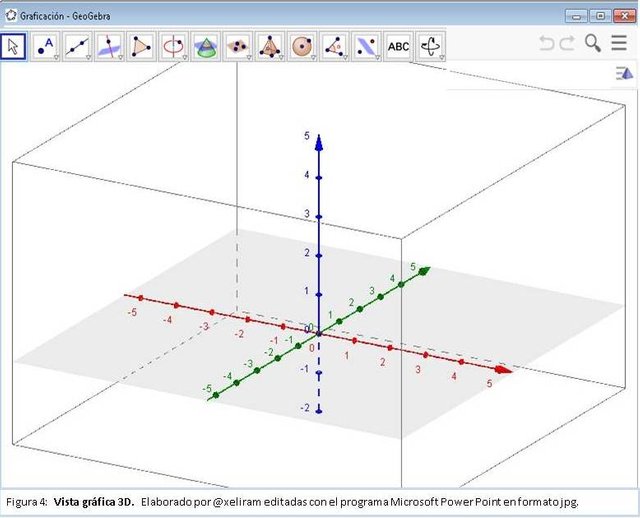
Barra de herramienta gráfica 3D.

Aquí disponemos de una nueva barra de herramientas, donde algunas íconos de esta barra son los mismos de la barra de herramienta anterior, que pueden utilizarse con el ratón, permitiendo las construcciones tridimensionales directamente en la vista grafica 3D. Al igual que la anterior, al hacer clic en cada ícono, se obtiene un menú desplegable con diferentes posibilidades.
Vista CAS
Permite realizar cálculos en forma simbólica, derivadas, integrales, sistemas de ecuaciones, cálculo matricial, entre otros, se comporta de forma similar a la línea de entrada, permite introducir expresiones y comando específicos, en el cual dispone de su propia barra de herramientas. La vista CAS se relaciona de forma dinámica con el resto del Geogebra y es fácil de usar (ver figura 5).
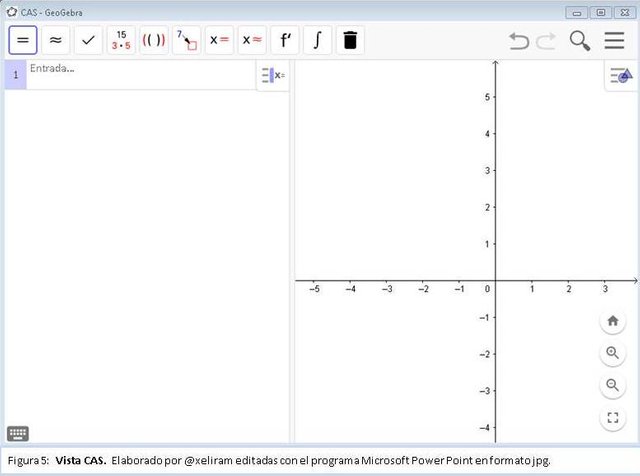
Barra de herramienta CAS.

Esta barra al igual que las anteriores se selecciona con el ratón, y sirven para evaluar expresiones ingresadas y realizar cálculos.
Vista Hoja de Cálculo
Esta vista, presenta una planilla con celdas organizadas en filas y columnas en las cuales es posible ingresar y tratar datos numéricos. También ofrece herramientas para el tratamiento estadístico de los datos. Muy similar al Excel y sus fórmulas numéricas, pero más potente, ya que se integra al entorno de geometría, permitiendo realizar iteraciones de construcciones. Los objetos creados en la vista hoja de cálculo aparecerán inmediatamente representados en la gráfica y también lo podremos ver en la vista algebraica (ver figura 6).
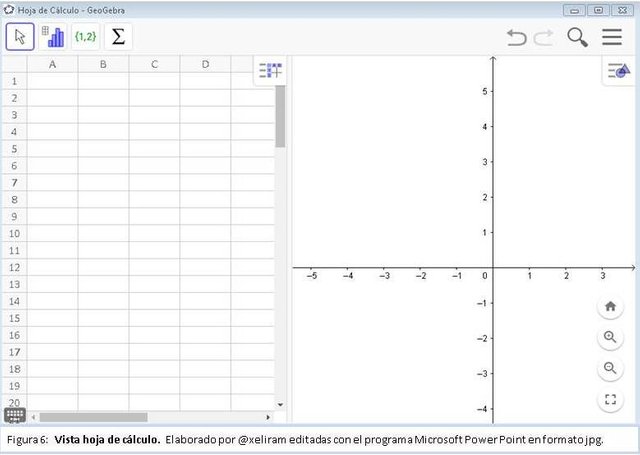
Barra de herramienta de la Hoja de Cálculo.
En esta barra de herramienta encontraras: herramientas de desplazamiento, herramienta de análisis de datos, herramientas de listas y tablas y herramientas de cálculos estadísticos.
REFERENCIAS CONSULTADAS
Galaz, M. (sf). Geogebra: una herramienta para la construcciones geométricas. Disponible:
Hohenwarter, M., Hohenwarter, J., Kreis, Y. y Lavicza, Z. (2008). Teaching and learning calculus with free dynamic mathematics software GeoGebra. 11th International Congress on Mathematical Education. Monterrey, Nuevo Leon, Mexico. Disponible: http://www.geogebra.org/publications/2008-ICME-TSG16-Calculus-GeoGebra-Paper.pdf
Losada, R (2007): “GeoGebra: La eficiencia de la intuición” en Gaceta de la RSME vol. 10.2, pp. 223-239.
Manual del Geogebra. Disponible: https://wiki.geogebra.org/es/Manual
Pérez, A. (2007). Centro Virtual de Divulgación de las matemáticas, DivulgaMAT. Disponible: http://divulgamat2.ehu.es/divulgamat15/index. 18/01/2011
Preiner, J. (2008). Dynamic Mathematics Software to Mathematics Teachers: the Case of GeoGebra. Salzburg. Faculty of Natural Sciences University of Salzburg. Recuperado de http://www.geogebra.org/publications/jpreiner-dissertation.pdf
Las imágenes son capturas de pantalla que pertenecen al software Geogebra 6.
Soy Marilex Porteles profesora de Matemática, investigadora, soñadora, me gusta tejer y nadar.
Para leer contenido de calidad sobre ciencia los invito a visitar la etiqueta #stem-espanol.
¡Hasta pronto!**











Muy bien. Las matemáticas son lo máximo :)
Posted using Partiko Android
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @emiliomorles, próximamente estaré realizando algunos ejercicios..
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail.
If you appreciate the work we are doing then consider voting us for witness by selecting stem.witness!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por el apoyo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit