Understanding Higher Dimensions of Reality - Sacred Geometry - Sacred Calculus - Sacred Mathematics - Hyperdimensions

If you could write a message that lasted forever, what would you say?

---

Image Source

In ancient times, you had to etch your messages deep into the stone and hope that someday someone would dig them up after you were long gone. Today it is now possible to etch your messages in a digital stone called the blockchain, and that message will remain long after you are gone. The message will remain as long as a civilization exists that has electricity and internet capabilities. Some seem to assume that one day the power grid will go out globally, but they fail to realize how easy it is to generate electricity with solar and wind. I personally think, that in an extreme situation, where the power grid goes down, people would be quick to start building small scale local grids.

Anyways, I think these messages will last on the blockchain for awhile, so what do I have to say to the people of the future?

There is a Divine Plan or Blueprint that you can align with to remain harmonious with the the world in which you live. Mathematics and geometry reveal the fingerprints, or clues, of this order. These patterns are beyond any dogma, religion, and tradition. They do not require faith, and can be easily verified by anyone who understands our base 10 number system and is equipped with a compass and a straight edge.

It's no joke you can literally derive absolutely every pattern, number, and equation in this universe with a simple compass and straight edge. This is the importance of Geometric Proofs.

Start with a blank slate or the void. Create a single point or the singularity before the big bang. Create a circle using your point as the center. LET THERE BE LIGHT! Now draw another circle using its center as any point of your first circle. Now you have duality, the vesica pisces, the stargate of creation. Make another circle using the intersection of the first two as your center point. This gives you the holy trinity that we hear so much about in certain religions. Go around your original circle and continue to draw circles at the intersection points. 6 circles will fit around your 1st one. This gives you the holy number 7, and also what is called the seed of life or the Genesis Pattern. Didn't it take God 7 Days, or circles, to create the universe in the book of Genesis? You can continue to expand this pattern and come to the flower of life, tree of life, metatron's cube, the 5 platonic solids, and eventually absolutely every template/key/blueprint that is needed to construct entire universes and galaxies. If you think this sounds crazy, maybe you should look at the pattern of all plants, life forms, and minerals.

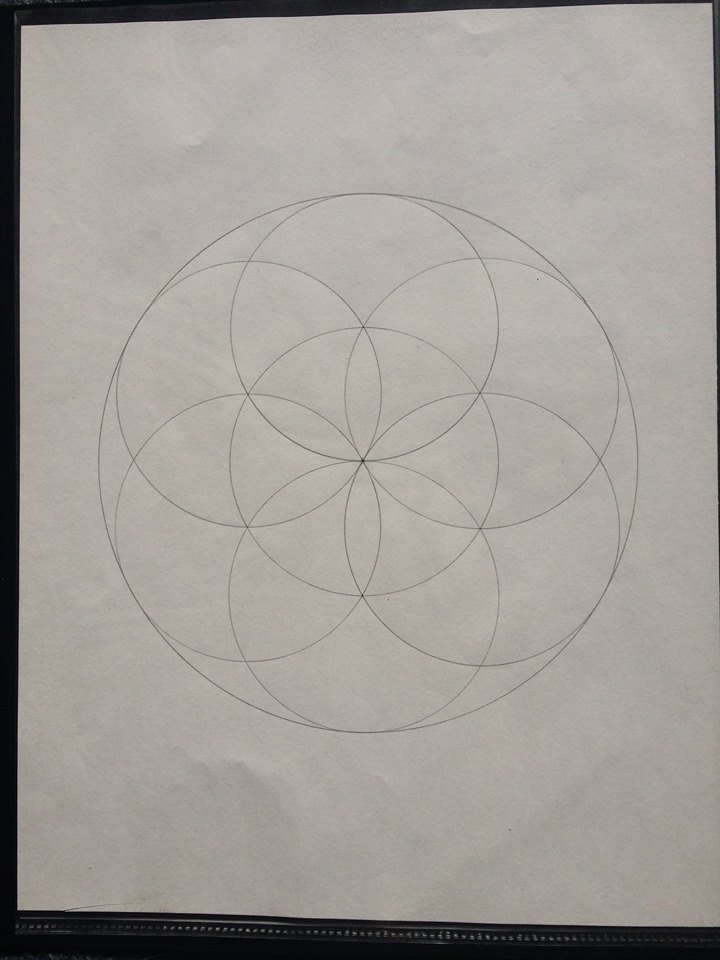
You can see a sample of my other personal drawings here:
http://crystalgeometry.weebly.com/sacred-geometry.html

I will go more into these patterns and sacred geometry in future posts, but for now let us return to the math..

The hard part for most people is that they were taught to despise and hate math. They came to the conclusion that math was hard simply because no teacher or school took the time to show them the harmony between number and nature. Math isn't simply a logical language of the left brain. Geometric Symbols are the key to bridging the right and left brain. Being shown these symbols and patterns within your natural world allows you to realize their importance. Math and numbers aren't solely meant to be used for counting and measuring how quickly you can extract a resource and profit from it. This is were our society has been led astray.

I find it absolutely mind boggling that many people have never learned any geometry or mathematics outside of the second dimension of planes. Maybe this is why our species is so lost and cannot fathom the existence of multiple dimensions beyond 3D. How can you conceptually understand 4D and beyond if noone ever taught you more than linear algebra and planar geometry. Many people have a hard time even visualizing three dimensional shapes.

What is a dimension anyways?

A measurable extent of some kind, such as length, breadth, depth, or height

I have always had an innate love for mathematics and science, which is why I decided to go into an Engineering major. It astounds how long our schools wait to show a student geometry and math beyond straight lines and planes. The majority of the population simply stops at linear algebra and planar geometry. Which keeps them trapped in the 1st and 2nd dimensions even though our observable reality obviously exists in at least 3 dimensions.

It isn't until Calculus 1 that you start to learn how to take the slope of a curve. This opens up the mind to things beyond linear thinking. The slope of a curve is also called an instantaneous rate of change. The mathematical operation of doing this is called a derivative. In linear algebra, the slope is found by picking two points and finding the rise over run, or simply the change in height over the change in width. With a derivative you find the slope with one point instead of two. But how is this possible? The key to this is understanding limits. If you understand how to take the slope of two points, now imagine that these two points come closer and closer together until the distance between them goes to zero. Eventually these two points are so close together that they appear to be the same point. So you take the slope of two points that have the distance of zero between them. Its mind bending right?

Hmmmm. These mathmagicians seem like wizards even though the patterns are there for any to follow.

Now what the hell is the point of taking the instantaneous rate of change or slope at a single point? Well if your equation or graph is the the change of position of an object relative to time, then the derivative or slope at a single point allows you to find the velocity of the object. You can take the derivative of a position graph and find its velocity. Then if you take the derivative again you have the acceleration. You can go further and take the derivative of the acceleration equation which will give you what's called jerk. The laymen would understand jerk as whiplash. We will leave it at that for the moment.

Have I lost you yet? Try to stay with me.

The reason you think math is pointless is because you were only taught the math of a line and a plane when your world is beyond both of those limitations. Break free from the projected shadow of 2D flat land and evolve into the next dimension. I promise we will get to 3D.....and discuss a bit beyond that.

But first lets talk about the opposite or inverse of a derivative called an integral. This leads us to Calculus 2.

All mathematical operations have an inverse or opposite. This may seem like a complex idea, but all it means is that there is an operation that can undo the operation that you performed. You already know this. Addition and Subtraction are the first example you learned. Then Multiplication and Division. Derivatives are to integrals as addition is to subtraction. So if you know somethings acceleration with respect to time you can take its integral and get back to its velocity equation. Take the integral of velocity and your back to displacement. Easy enough?

So what other purpose does this have?

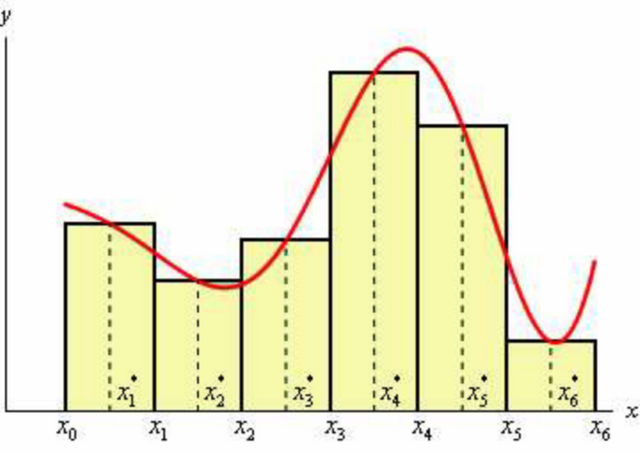
With integrals we can find the area under a curve which means we can find equations for the area of any irregular shape in the world. If we have a shapes equation we can take its integral and have its area equation. Pretty cool huh? But how is this done? Once again we have to stretch the mind and think of limits. To estimate the area under a graph we can simply draw rectangles underneath it, since all of us know a standard equation for the area of a rectangle, and simply add the area of the rectangles together. To make your approximation better you can draw rectangles with smaller and smaller widths until the width of the rectangle is approaching zero. Basically just imagine that you are drawing an infinite amount of teeny tiny rectangles and then adding that area up. Boom you now understand integration.

Image Source

But now even though you grasp the basics of Calculus 1 and Calculus 2, at least in theory, you are still only dealing with the second dimension. What use is it to understand how to calculate area of any shape in 2D when we live in 3D?

It wasn't until Calculus 3 that I began learning about the 3rd Dimension. Yes, I admit, that there were mentions of a Z axis before this when volume is discussed, but the major focus was always on an X-Y plane.

That's right our society thinks it is a good idea to wait and teach you about 3D math after you've already decided that it was absolutely useless in the real world.
The problem is almost no one makes it to Calculus 3.

So to step into the third dimension you go add another axis called the Z axis that is perpendicular to the XY plane. If that sounds fancy just imagine a square on your page popping out towards you to make a cube. The basics of Calculus 3 just allow us to take derivatives and integrals in this 3D space. This is done by taking partial integrals and derivatives with respect to different variables and planes. I won't try to explain this in detail, as I have a hard time putting it into words.

What does this allow us to do?

Instead of finding just the area of an irregular shape we can now find the volume of any irregular shape in the world. Instead of just finding the position, velocity, and acceleration in 2 Dimensions we can now do it in 3 Dimensions. We can not only travel left-right, forward-backward, but we can also now travel up-down.

We can now actually apply math to the reality we live in!

Beyond the 3rd Dimension....

Many people seem to think that we only live in 3 dimensions even if they don't fully understand the math of how all of this works. However, geometry is not limited to 3 dimensions, and neither is your life. If you don't believe me, I ask you to consider two things: Time & Dreams. Some consider time as the fourth dimension and stop there, but where are we when we are dreaming? We obviously experience another dimension even when our eyes are closed and our body is at rest. Do we consider this the 5th dimension of out-in? Why stop just at the 5th dimension? Geometry doesn't stop there even if your mind cannot visualize it or rationalize it. Dreams are an important door to other dimensions. Lucid dreaming is the process of mastering these hyperdimensions. Just as a hypercube casts a 3D shadow of a cube, and a cube casts a 2D shadow of a square, your idea of a 3D self is just a shadow of the higher dimensions. You can easily imagine a 2D shadow of yourself on the ground, but can you begin to go up the dimensional scale and imagine your self in 4D, 5D, and beyond?

What about the hypercube, hypertetrahedron, hyperdodecahedron? Astral Geometric Light Body Vehicles?

We will leave this topic upon until next time :)