블랙홀의 존재에 대한 슈뢰딩거 방정식의 도입에 의한 양자점과 특이점 수학적 고찰
블랙홀과 화이트홀은 연결되어 있으면서 그 사이 웜홀이 있어서 시간여행이 가능하게 만들어 준다. 그런데 우리는 블랙홀의 위치와 존재 범위에 대해서 막연히 추측만 할 뿐 그 존재에 대해서는 어떤 논리적인 공식을 유도해 내지 못하고 있다.
미시 양자역학과 거시 우주 사이에 일관적으로 적용되는 신의 원칙이 있다면 그건 반드시 하나의 통일장이론으로 그 가치를 발할 것이다.
나는 블랙홀의 위치에 대한 여러 가지 생각을 하던 중 한 가지 생각에 정신이 집중되었다. 빛이 파동이라면 아인슈타인의 상대성이론에 의하면 중력장이 강한 물체의 주변을 지나갈 때 휘어지게 되고 블랙홀에서는 사건의지평면에서 특이점구간에서 빛은 빠져나가지 못한다.
그런데 우주의 임계밀도를 유지하기 위해서는 블랙홀에 들어온 양만큼의 질량이 화이트홀을 통해 빠져 나가야 된다. 그럼 블랙홀은 우주의 어디에 존재하고 어떤 특성을 가지면서 움직이고 어떤 공식에 의해서 세기의 변화가 나타날까?
고민 끝에 난 하나의 가설을 설정했다.
즉, 파동은 제한된 공간속에서 양자화되어 있다. 우주의 크기가 무한이 아니라면 이 원칙은 양자세계에서 우주에도 적용할 수 있다는 착상이 떠올랐다. 갇힌 전자의 파동함수를 빛의 블랙홀 속에서의 파동함수로 식을 변형시켜서 유한한 우물 깊이에 해당되는 블랙홀의 사건의 지평면에서 특이점까지의 방정식은 d²ψ/dx²+8π²m[E-U(x)]ψ /h²=0로 대체하고 이를 풀면 확률밀도함수ψ²n(x)를 나타내는 그래프가 나온다. 그리고 2,3차원의 슈뢰딩거 방정식을 접목하여 특이점의 안정점을 계산할 수 있고, 이를 토대로 화이트홀의 위치를 계산할 수 있다. 아직은 조금 불안정한 면이 많은데 충분한 시간을 두고 정리를 할 생각이다. 이것이 해결되면 시공간에 대한 블랙홀의 위치와 개수등을 쉽게 계산 할수 있다. 한마디로 특이점을 양자점으로 전이시키는 것이다. 참고로 수소원자의 퍼텐셜 우물에 대한 에너지 함수공식과 그래프는 다음과 같이 나타난다.
U(r)=-e²/4π₀r 에 의해서 다음 그림을 그릴 수 있다. 얼마나 블랙홀과 모습이 닮았나?
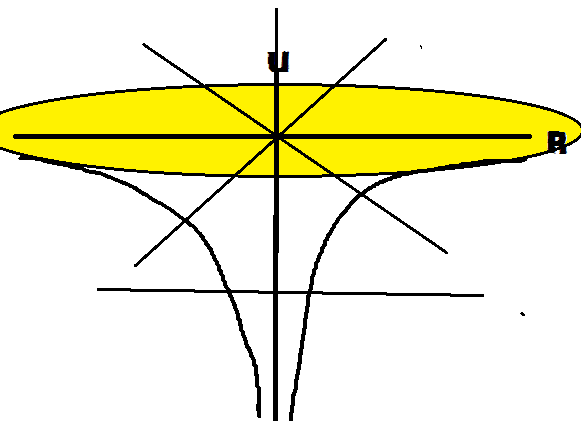
이건 유레카를 수백번 외쳐도 계속외쳐야 될 내용이다.
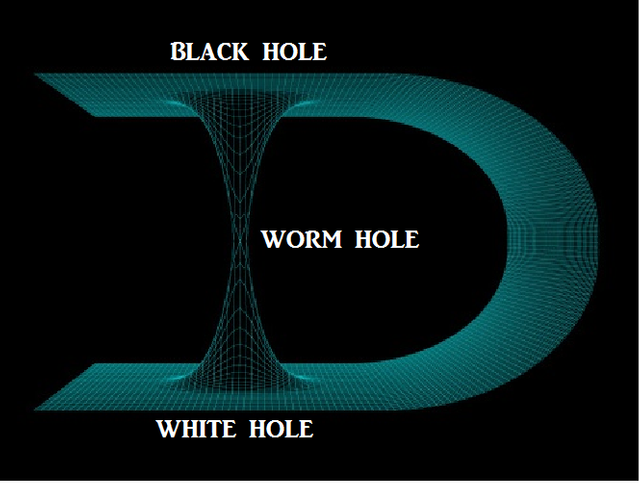
이 글의 출처는 '22세기 수학과학 institute ' 에서 가져온 내용입니다.
==============
재밌게 읽으셨다면 감사하겠습니다.
글을 스크랩 또는 다른 곳에 올리신다면 제 스팀잇 주소를 마지막에 출처를 밝혀 주시면 감사하겠습니다^^
https://steemit.com/kr/@economy
Please Follow @economy 
오류가 있으면 지적해주시면 감사하겠습니다.
이해는 안 되지만 흥미롭습니다. 다음 글도 기대하겠습니다~^^
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
재미있어요
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
재밌다니 ... 엄청나신듯! 종종 글올릴게요. 감사합니다.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit