#STEEMGIGS: (tutorials) — I will offer some Math Tutorial Subjects. I will teach you on how to solve it.

I will share some simple math problems. If you want to tutor some math problems I am willing to teach you. This is related to my course which is Electrical Engineering. In engineering courses and other related fields was more on mathematics subject.

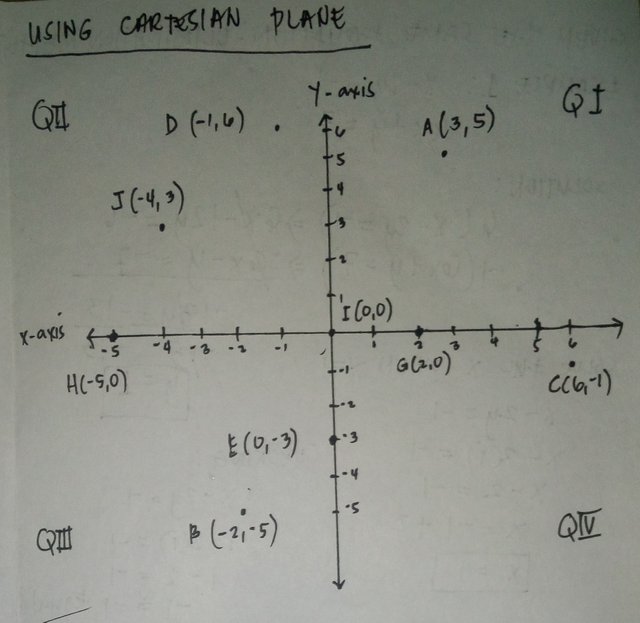
Using a CARTESIAN COORDINATE PLANE.

The given coordinate plane below, I want to plot the following points and I will label the points base on the given.

A. (3,5)

B. (-2,-5)

C.(6,1)

D.(-1,6)

E. (0,-3)

F. (4,-6)

G. (2,0)

H. (-5,0)

I. (0,0)

J. (-4,3)

•Rewriting in Ax+By=C into the form of y=mx+b and vice versa.

An Ax+By=C is standard form in linear equation in two variables which is the x and y. Any linear equation can be transformed into its corresponding slope-intercept form or y=mx+b. The m means a SLOPE while b is the Y-INTERCEPT.

This can be rewrite to the following into a form of y=mx+b. Transpose the other variables into the right side.

The Quadratic Equations 

Concept: Solving a systems of equations by using a SUBSTITUTION METHOD.

The Quadratic Equations 

Concept: Solving a systems of equations by using a ELIMINATION METHOD.

The Quadratic Equations

Concept : Identifying Linear and Quadratic Equations

A quadratic equation in one variable is of the form in ax^2+bx+c=0 where a,b and c are called as real numbers and a ≠0. A complete quadratic equation contains both teh first and second power of x and while an incomplete contains the second power of x and y. The linear equation in one variable contains the first power of the variable.

The Quadratic Equations

Concept: Solving by Extracting the Square Root Method.

This is an incomplete quadratic equation is in form of ax^2+c=0 where a ≠0. To solve on this sample below , I need to transpose c and it will divided by a then extract the square root of both members of the equation. Any quadratic equation has two roots.

• To solve for the roots of the following incomplete quadratic equations by extracting the square root and also to identify the roots as a real or nonreal , rational and irrational, equal and unequal.

The Quadratic Equations 

Concept: Solving a systems of equations by using a FACTORING METHOD

Solving the quadratic equation by FACTORING METHOD. It will simplify and equate the trinomial to zero then factor. Apply the zero product property of real numbers . A product of two real numbers are zero unless if at least one of the factors is zero, conversely, then if the product of two real numbers are zero then either factor is zero or both factors are each equal to zero.

The Quadratic Equations 

Concept: Using the Completing the Square Method

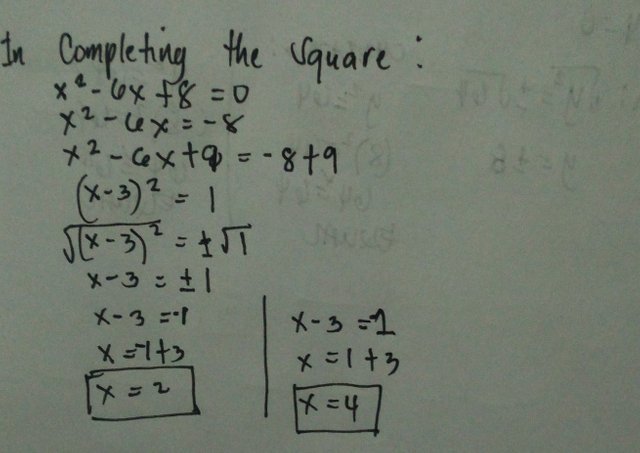
To express the equation in the form of ax^2+bx=c.

•Add a term to each of the following to make it perfect square trinomial and it will express it as a binomial square. 

The Quadratic Equations

Concept: Quadratic Formula Method.

The formula of Quadratic Equation is derived from the standard form of : ax^2+bx+c=0 and using it as a completing the square the result was :

• We need to rewrite the following equations in the standard form the identify the value of a,b,c then substitute in the formula and solve for the roots.

In Quadratic Equations:

Concept : The Nature of the Roots of a Quadratic Equation

In the quadratic formula the radicand b^2-4ac is called the discriminant . The numerical values tells us on what kind of root the quadratic equation has, if the formula b^2-4ac is:

1.ZERO - roots are equal, rational ,real.

2.POSITIVE: 

    Perfect square - roots are unequal, rational , real.

3.NEGATIVE- roots are nonreal.

•Determine the nature of the roots of the following quadratic equations by solving for value of the discriminant which is the b^2-4ac.

A RATIONAL EXPRESSIONS

Concept: Operation with Rational Numbers

•Example:

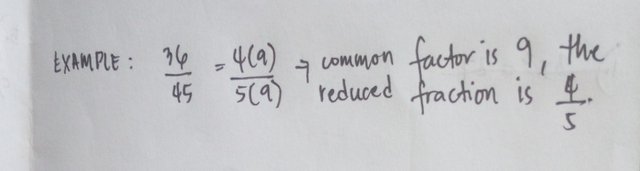
A rational number is a number which can express in form a/b where b≠0. A rational number or rational expression is in its simplest form when both numerator and denominator do not contain a common factor or expression is a relatively a prime.

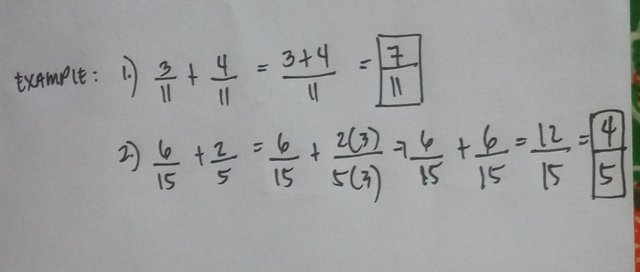
A Rational numbers or fractions can be subtracted ,added , multiplied and even divided. When the fractions have same denominators, you will add the numerator and it will simply copy the denominator. To reduce the fractions to its simplest form. When the denominators are not equal then it will be expressed it to the given fractions to its equivalent form.

A Rational Algebraic Expression

Concept: Reducing Rational Expressions

Fractional is known as a rational number. When numerator or denominator contains a variable or variables. This rational number becomes a rational algebraic expression. The rational expressions must be reduced to lowest term ,that was removing the common factor. This common factor is called as GCF or known as Greatest Common Factor.

This example shows the factory in both numerator and denominator. One factor must be the GCF of both. No denominator is zero.

A Rational Algebraic Expressions

Concept: Sum & Difference of Rational Expressions

When the fractions are similar and it simplys add the numerator and to copy the common denominator.

A Rational Algebraic Expressions

Concept: Product of Rational Expressions.

To factor both numerator and denominator. Cancel the common factors and then multiply.

•The product in its simplest form. It was assumed that none of the denominators is zero. It shows the cancelled factors in this sample.

A Rational Algebraic Expressions

Concept: Quotients of Rational Expressions

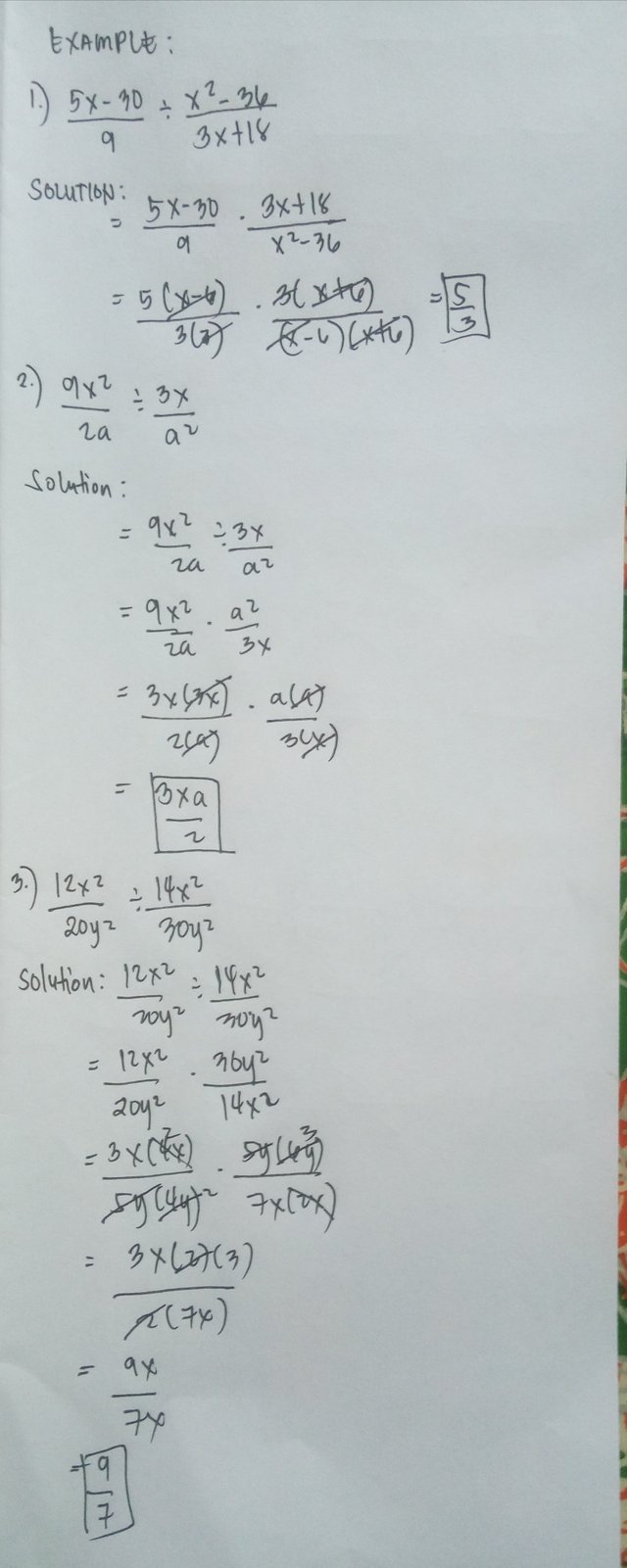
Divide the rational expressions and it will simply follow the rules for dividing fractions that was get the reciprocal of the divisor and it will apply the rules for multiplication of fractions.

Example in finding the quotient in its simplest form.