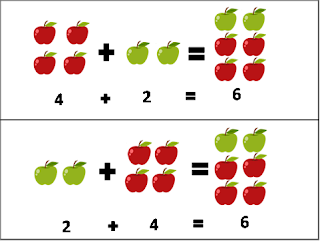
"Multiplication is an operation that belongs to the family of the sum". At least this affirmation that we have maintained for years as the only way to approach this operation. Do we review any strategy?
Source
When we work on the construction of this concept, we must take into account the relationship between multiplication and other operations, not only its relation to the sum, we will see that many multiplicative situations can also be resolved with divisions or subtractions.

Source
Knowing that "multiply" is not related exclusively to the resolution of its operative calculation, but to the world of significations that involve the operation.
Our students will know how to multiply when in addition to knowing that the calculation can apply it in the proposed situations and recognize the operation in the declarations of the activities.
Many times we propose the teaching of multiplication from the repeated addition of quantities.
How many have in total if each package brings 10?
Possibly our students add 10 + 10 + 10 + 10 + 10 to achieve the result. It is in this case that the sum can be replaced by multiplication, as an economic form of calculation, performing 5 "times" 10 when the multiplication table was already included as a tool.
But what happens if this situation is reversed?
How many each package brings, if they all contain the same amount.
The resolution can go through different times, although it can be resolved with the division (50/10 = 50) that our students can look for, by way of equation, which number multiplied by 5 gives 50. This situation is also multiplicative.
Another way to present it would be:
How many packages will Manuel have bought if in total he has 50 figurines?
To solve it we can resort to subtraction as an operation, since we can increase 50 - 10 - 10 - 10 - 10 - 10 and get to the result: if I subtracted five times the amount of each package, then I bought five packages, because 5 X 10 It's fifty.
Therefore, as we can see, a multiplicative situation can be solved with different strategies, so it is important to analyze all the possibilities generated by a situation and discover, together with the group, different resolution strategies.
MULTIPLICATION TABLES: a separate theme
It often happens that the "amount" of mathematics that a child knows by a very particular parameter is generally measured socially: the tables.

Source
In this sense, it is important to note that the multiplication tables are a valuable tool to accelerate the calculation and that it is important that our students manage to internalize them and use them in mental calculations, but not as a mere repetition but as the construction of an instrument that will facilitate the calculation.
To favor this construction, students must operate with concrete material building proportional tables.
When MULTIPLICATION is a repeated sum of quantities.
If we have several figures and we want to know how many are, we can perform two procedures. First, count them one by one or, if they present a regularly ordered disposition. What is simpler and faster is to operate numerically: add or, better yet, multiply.
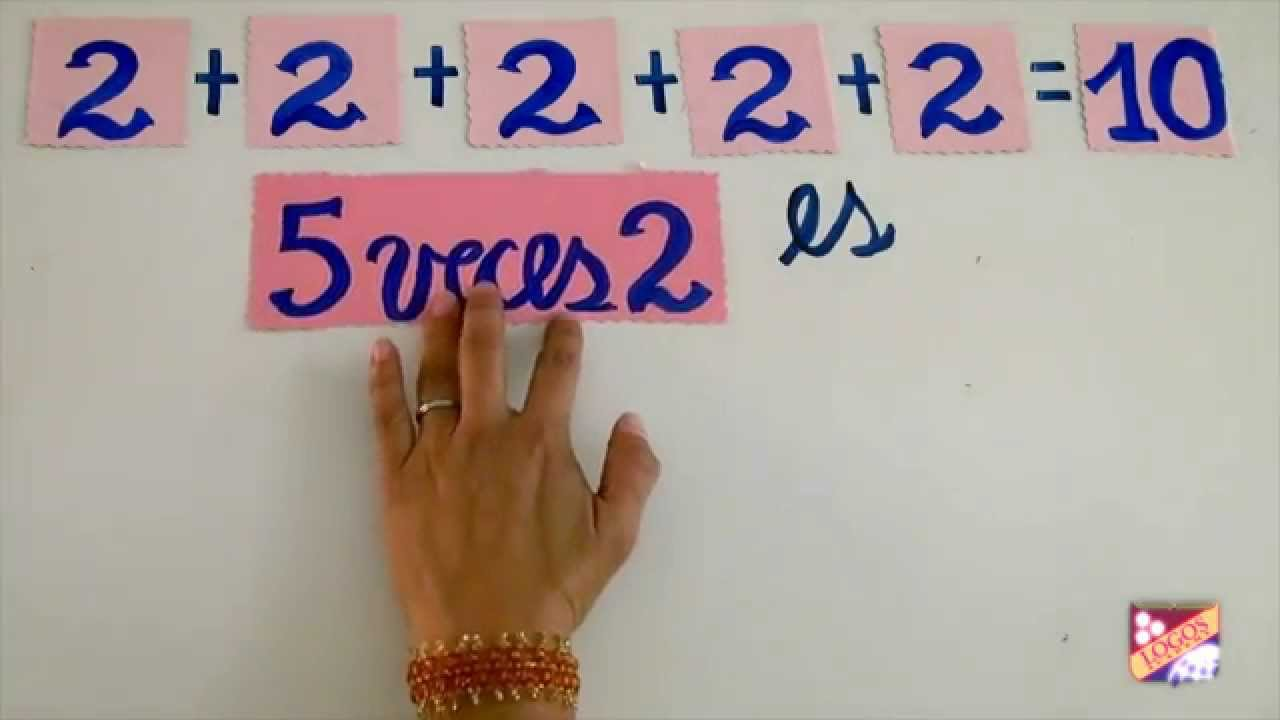
Source
In order for children to discover these quantification strategies, we must propose a problematic situation that aims to discover that meaning.
Reference:
https://www.gcfaprendelibre.org/matematicas/curso/multiplicacion_y_division.do
https://www.etapainfantil.com/ensenar-tablas-multiplicar
Another cool thing.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks friend
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
good tutorial, sharing this on twitter
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks friend
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is nice, think i can adapt this to teach my daughter maths!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Having a solid understanding of the fundamentals of math is so important. There are so many relationships between mathematical operations and even just the numbers themselves. Conducting math talks in your class and talking through these relationships can really help to develop stronger understanding in our students. If we show a passion for numbers and math it will transfer over to our students.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You are right in:
We must be the first to show our interest to the students.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is a very good post. I admire those who can explain essential mathematics to the very young. It's a talent I admittedly have never developed. I must admit that I envy those who can do it.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
It's easy, working with children, I can tell you better than with adults. I worked with adults instead of children, and I stay with children who are easy to learn. The game is the best strategy for them.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
For me, it's younger children (Year 1 through Year 6), then first year university students, then older high school. The middle years students tend to be hit or miss, until they realize that they need you to write them a good recommendation.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit