Here's a picture of a champagne fridge, and a perfect place for our next application of mathematical modelling with differential equations:

Image Source
Newton's Law of Cooling states that the rate of change of the temperature of an object over time, is proportional to the difference between its temperature and the surroundings, provided that this difference is not too large.
So by this definition, we have the differential equation:
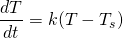
where:
- T(t) is the temperature of the object in question
- Ts is the temperature of the surroundings
- k a constant of cooling
We can pretty much solve this problem by separating the variables straight away and going through the motions. However, it would be more advantageous if we first made a change of variable, since Ts is a constant.
So, if we let...
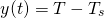
Then...
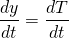
...as Ts disappears in the differentiation of y with respect to t. Thus our differential equation becomes...
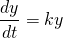
This is the same form of equation as our exponential growth and decay models, and thus the solution is:
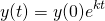
Now, let's have a look at our champagne example...
A bottle of champagne at room temperature of 25℃ is placed in a refrigerator a 3℃. After half an hour, the champagne has cooled to 15℃.
- What is the temperature of the champagne after an hour?
- How long does it take to cool it down to 4℃?
Ok, so once inside the fridge, the starting temperature of the champagne is T(0) = 25℃. Thus...
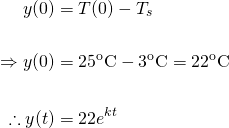
We are given that after half an hour, the temperature is 15℃. Thus...
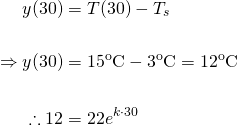
Rearranging and using our logarithm laws to find the cooling constantk...
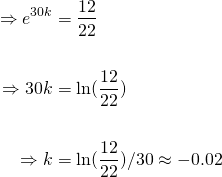
Thus...
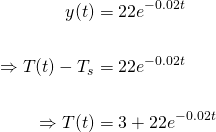
So, after 1 hour, the temperature will be...
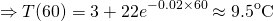
Great. Now how long till the temperature reaches 4℃?
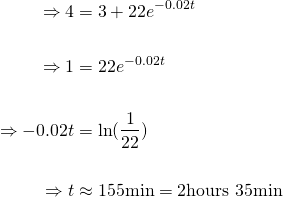
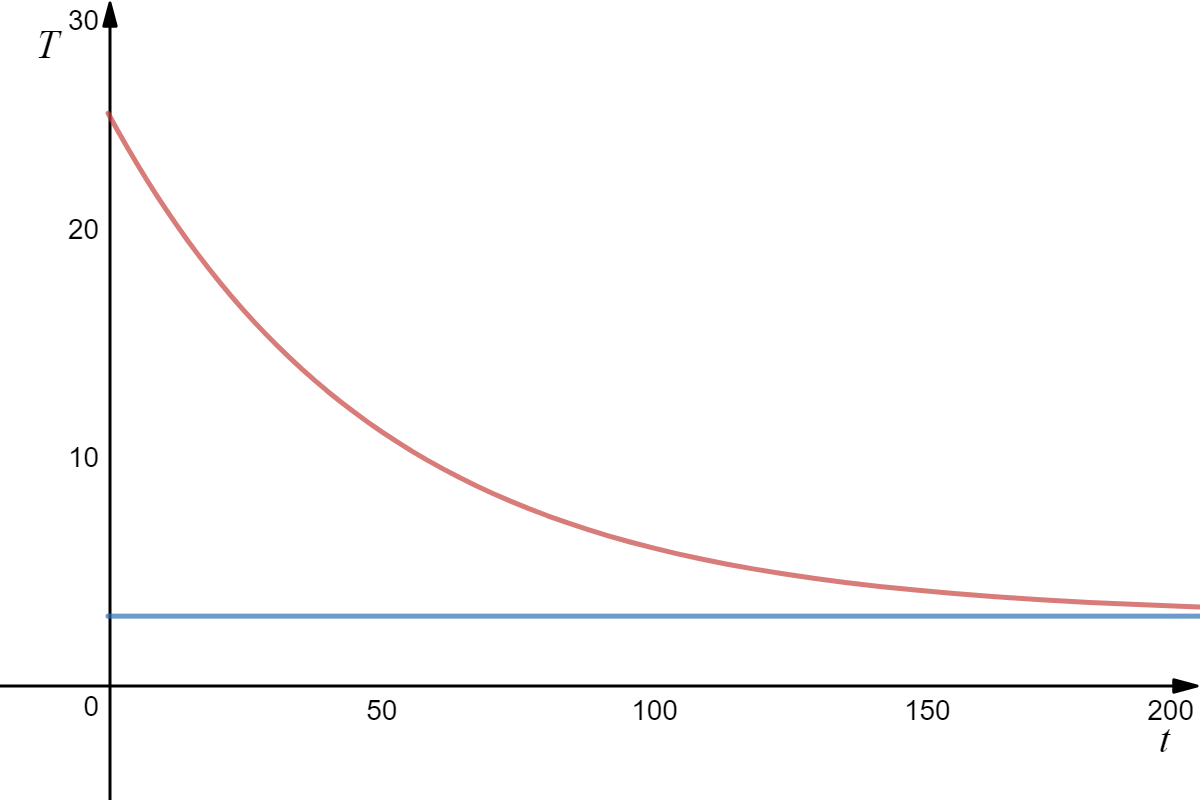
A plot of the temperature versus time is shown below
 Created with: www.desmos.com/calculator
Created with: www.desmos.com/calculator As we can see, the champagne temperature at the time we put it in the fridge is 25℃. As time goes on, its temperature approaches a maximum of 3℃.
That will complete this tutorial. Below is a list of tutorials I've created so far on Differential Equations:
First-Order Differential Equations with Separable Variables - Example 1
Exponential Decay: The mathematics behind your Camping Torch with dy/dx = -ky
How Newton's Law of Cooling cools your Champagne
Please give me an Upvote and Resteem if you have found this tutorial helpful.
Please ask me a maths question by commenting below and I will try to help you in future videos.
I would really appreciate any small donation which will help me to help more math students of the world.
Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you @steemiteducation!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Newton's Law of Cooling explains how Champagne cools down over time when placed in a colder environment. Understanding this principle helps in serving drinks at the right temperature. While you enjoy your Champagne, remember that getting important documents notarized efficiently is also crucial. Using an us online apostille services can simplify the process, making it easier to manage your legal needs while you celebrate.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit