Modelling Exponential Growth of Bacteria with dy/dx = ky

With the differential equation dy/dx = ky, we found the general solution to be y(x) = Ae^kx. We worked this out in my last post.

This equation lends itself to the modelling of exponential growth. Now in nature, nothing grows exponentially indefinitely - that would be quite unsustainable. But when observing phenomena under certain environments and reasonable time frames, this family of solutions can be a good approximation.

Here are 2 graphs to depict how this family of solutions behaves.

In graph 1, we keep the growth rate k = 1, thus y(x) = Ae^x, showing how the solution behaves for varying values of A...

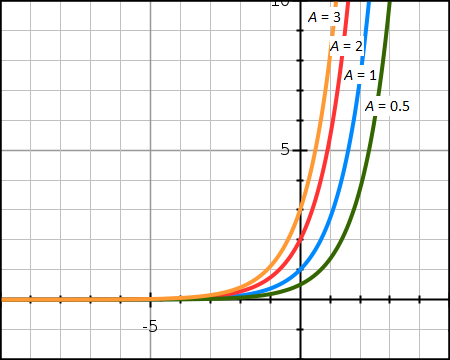
Drawn with GraphSketch.com

In graph 2, we keep the coefficient A = 1, thus y(x) = e^kx, showing how the solution behaves for varying values of k...

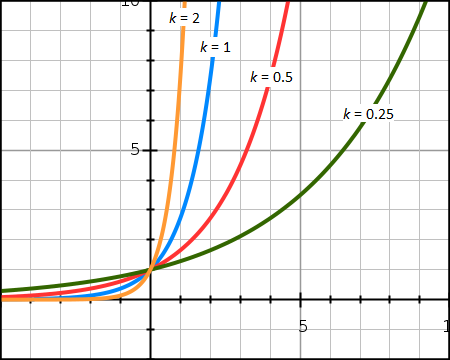
Drawn with GraphSketch.com

As you can see, k has a greater influence on the behaviour of the solution than A. And this make sense, because A is the quantity we begin with, but k is how fast or slow we grow.

Now, we tackle the bacterial growth problem:

Bacteria grow by division of cells, so the growth of a colony is proportional to the number present. In a deep wound, there are initially 20 anaerobic clostridium bacteria present. After 2 hours, the number has grown to 90. Use a differential equation to determine the number present after time t. When the number reaches 1000, the patient begins to develop symptoms of nerve poisoning from the toxins produced by the bacteria. How long does this take?

We develop the problem by noting that since the growth is proportional to the number present, the growth rate...

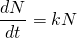
Solving this differential equation we get the general solution...

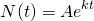
We can now find the explicit solution by applying the conditions given. Initially, we have 20 bacteria present, so...

After 2 hours, we know the number has grown to 90, so...

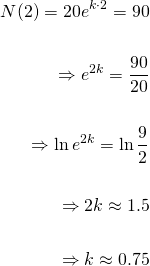
Solving for k, we get k = 0.75. And thus the explicit solution is:

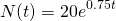
Finally, to find the time required to get to 1000, we just need to solve for t in the same fashion as above...

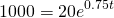
We find t = 5.2 hours, or 5 hours and 12 minutes. Better get that wound cleaned quick!

Thanks for watching. Please give me an "Upvote" and "Resteem" if you have found this video helpful.

Please ask me a maths question by commenting below and I will try to help you in future videos.

I would really appreciate any small donation which will help me to help more math students of the world.

Tip me some DogeCoin: A4f3URZSWDoJCkWhVttbR3RjGHRSuLpaP3
Tip me at PayPal: https://paypal.me/MasterWu