Arithmetic sequence is a sequence of terms with a common difference (denoted as d) between consecutive terms. For example, 2, 4, 6, 8, 10, ... is a sequence with 2 as the common difference. To get the common difference, subtract (4-2 = 2) ; (6-4 = 2) ;
(8-6 = 2) ; (10-8 = 2), so d=2.
To find the value of any term from a given arithmetic sequence, use the formula below.
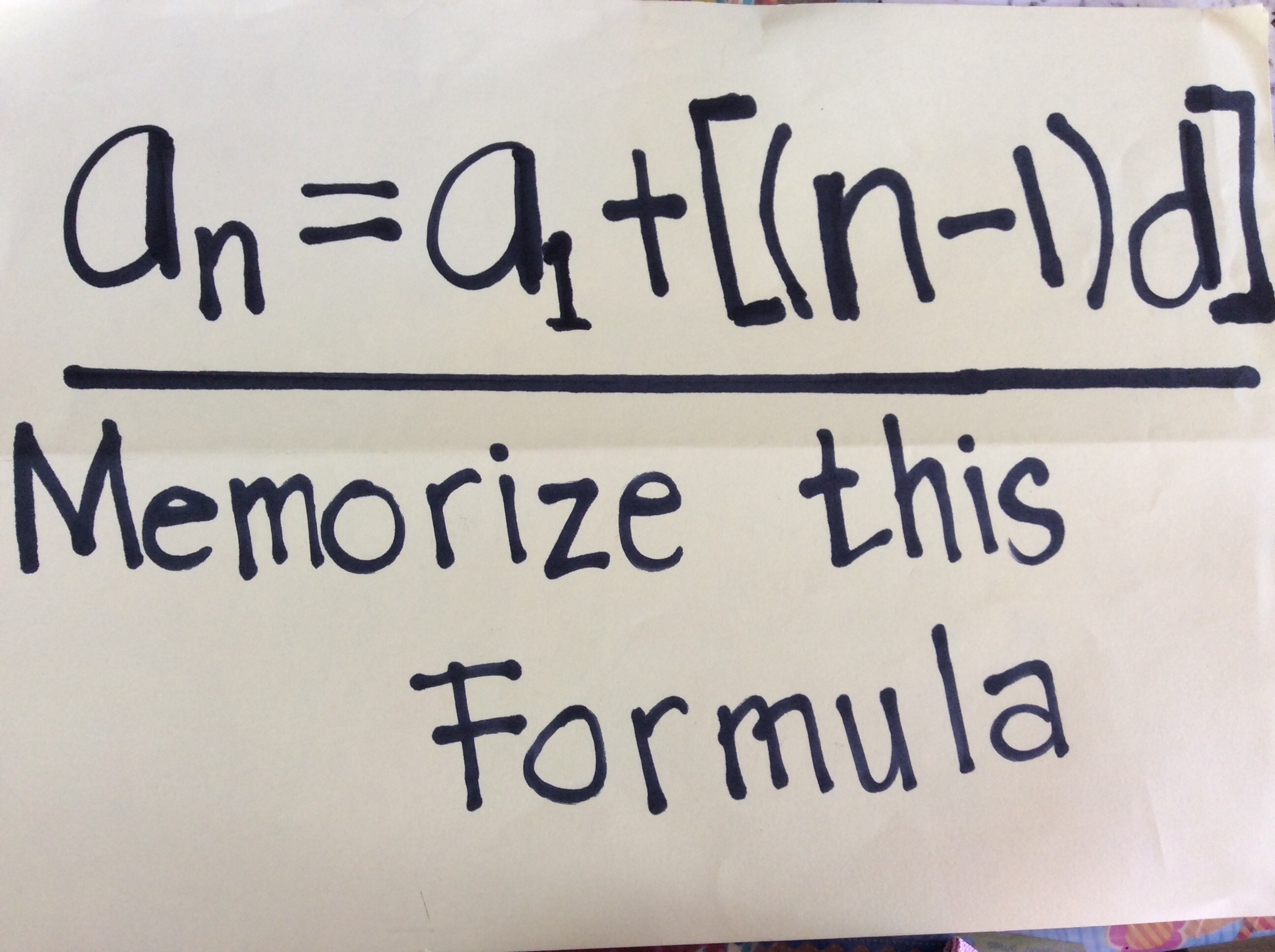
where ;

Let us try to answer these example and find the 20th term of the sequence.

To find the 20th term of the given sequence:
- Identify the first term and the nth term,
- Find the common difference exists between consecutive terms, and
- Substitute to the formula.
SOLUTION:
- First term = 6
- nth term = 20
- d = 4

Therefore, the 20th term is equal to 82.
- If you understood how to find the arithmetic sequence of an nth term, try to find the 33rd term of the given sequence below and drop your answer in the comments.
0.5 , 2.0 , 3.5 , 5.0 , ...
MathFun @rezel