Claudius Ptolemy was born in Egypt 100 years ago. He was a writer in profession. And there was astrology, mathematics. He also echoes the design of a solar system in the center of the earth. Despite his mistake, his suggestion helps in future research!
In the ninth-tenth class higher mathematical book we have come to see Ptolemy's theorem or many "seeing". Today, we will talk about Ptolemy's famous theorem, a little bit more!
The theorem was:"The sum of the area of rectangular rectangle in the opposite arms of a quadrilateral in the circle is equal to the rectangle within the corners of the quadrilateral. "
If you have difficulty understanding, look at the picture below
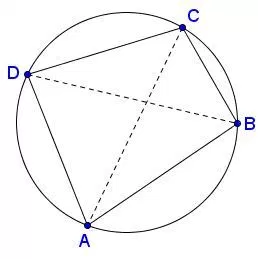
What is Ptolemy theorem, if we add AD * BC and CD * AB, then it will be equal to AC * BD. The condition is one, you can see the quadrilateral, it must be located inside a circle in such a way that it touches four to four top circles . It will not be said in the face, it will prove to be proved. Let's turn from the most beautiful part of this theorem. (Actually, the most beautiful and costly part of any theorem is its proof, evidence is never boring, it is proved by bowling.
Proof
The first thing I will do is take the angle DCE to the angle ACB equals. Look at the picture, this cartoon has been removed with a red spot.
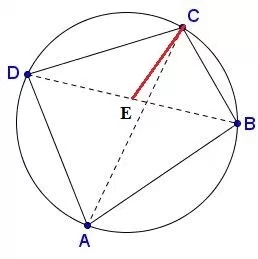
Again, who is the circle angle standing on BC? Yes, just say, angle BAC and angle BDC. Therefore, they are equal.
Now, between the triangle ABC and the triangle CDE,
Angle ACB = angle DCE
Angle BAC = angle BDC
Therefore, the triangle has two identical zodiac signs.
So from here we can say,
CD / CA = ED / BA => CD * BA = AC * ED --- (1)
Likewise,
Try to prove triangle BCE and triangle ACD like the triangles, try it. The same thing, just a symmetric matter!
From here,
BC/AC = BE/AD => BCAD = ACBE ———(2)
(1) and (2) add,
BCAD+CDAB = AC(BE+ED) = ACBD
Prove to end.
Come on, let's see some of the things that went to school at Sundaramo Avoyad. You do not know whether or not you know this Ptolemy theorem can be very good to prove Pythagoras' theorem. Do not waste time to see it
Take over, the quadrilateral is a rectangle. Imagine the picture, if your imagination is like the picture below, then I am fine.
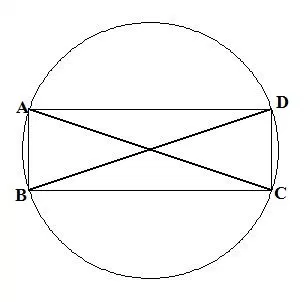
What is the Ptolemy theorem?
Ptolemy says:
ABDC + ADBC = AC*BD
Since it is a rectangle, its opposite arms are equal to each other! So let's say AB = DC and AD = BC, even the corners are equal to each other! Therefore, AC = BD.
Put these values in the upper equation,
Come see another interesting thing. Do you know, the circle / cubes of the pentagon = the golden rays ?
Come see a circle pentagon
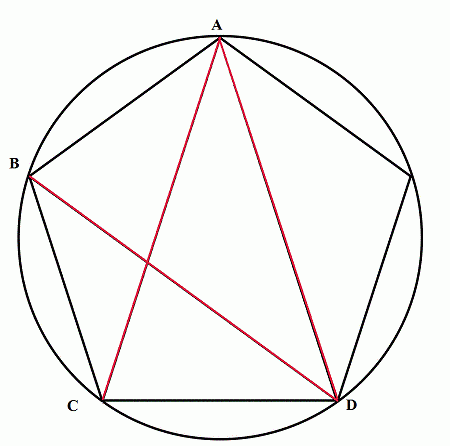
This pentagon is a regular Pentagon, whose five sides are equal. The ears of a regular Pentagon are the same, just as it is for a class, so they are all equal to AD, AC, BD (colored in red color).
The quadrilateral is inscribed in the ABCD circle, so Ptolemy's theorem can be said:
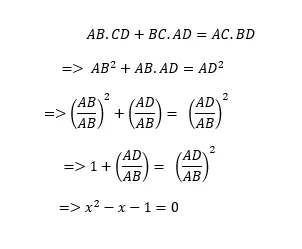 !
!
Use the condition that the second line is the same as the arm and the ears. And the next line is divided by AB ^ 2. Finally, I have assumed the AD / AB as x.
Have you seen this equation before? One solution to this equation is (1 + sqrt (5)) / 2 which we call golden rays
That means, a regular Pentagon's ears and one arm ratio are golden rays! Proven by Ptolemy The boring (!) Ptolemy theorem of the school college
Off topic: If the quadrilateral is not inscribed in the circle, that is, if some part of the circle goes out, then the relationship between the arm and the ear is determined by using Ptolemy inequality. It's like that

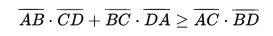
Next Discussion About of Golden Ratio
No.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I totally agree with you: 100 AD is not 100 years ago :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Pls vote and follow me toushik
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @toushik! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit