This is a seemingly mind-boggling primary school mathematics problem from Singapore, for primary 4, or even primary 3. This is like our version of grade 4 elementary school, but on steroids. You may want to call it “Singapore math”, but in Singapore, we just call it “maths”. Some of us pronounce it, improperly, as “macks”.
ABCD is a square of side 10 cm and PQR is a right-angled triangle. The corner P of triangle PQR is placed at the centre of square ABCD. BX = 3 cm. Find the area of the quadrilateral PXCY.
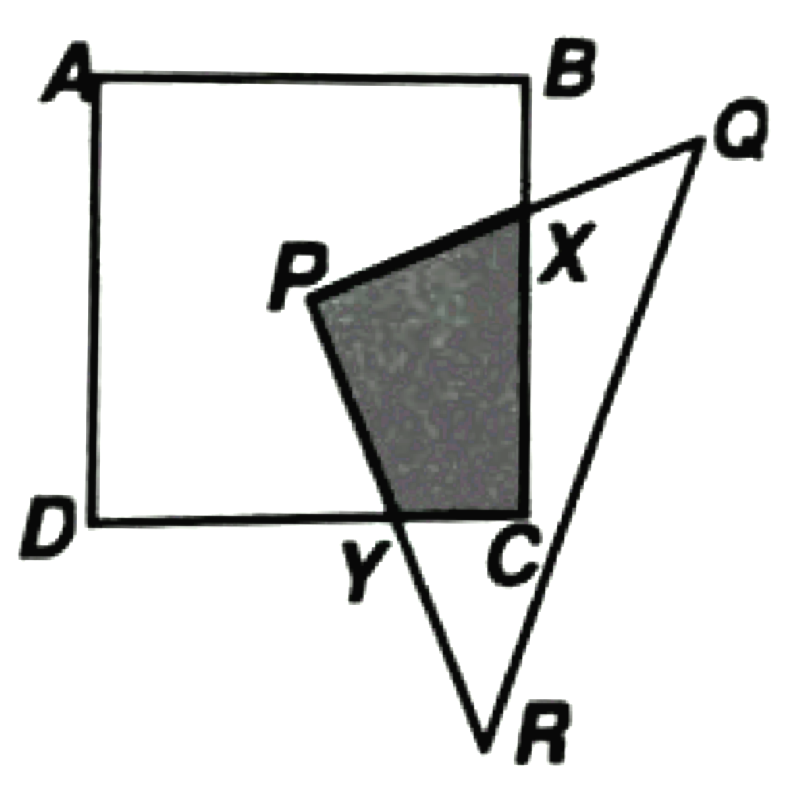
Challenging, eh?
How would you tackle this?
How do you begin?
Pause here.
Do not peep below.
Think about it.
Hint 1: Think of an equivalent problem (this is a heuristic).
Hint 2: Can you do things to the shape that does not change the area?
What we can do is to make an imaginary cut from P horizontally to the right, perpendicularly to BC. We get a piece in the shape of a right-angled triangle. We can take this right-angled triangle and move it down to re-join the shaded area at the lower side DC. (see diagram below). This looks like a rotation about P. We are just shifting the piece around, which does not change the area. But now the problem becomes really easy. It is just a quarter (or a fourth) of the big square ABCD! So it is ¼ × 10 × 10 or 25 cm².
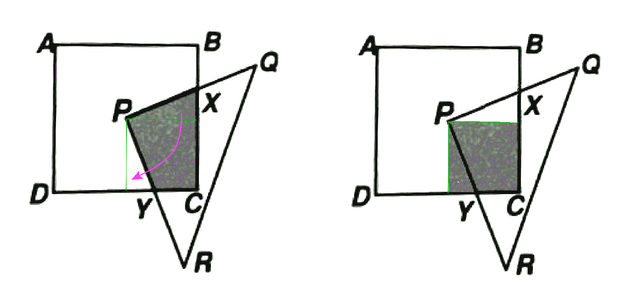
Notice that the fact that BX = 3 cm is irrelevant. If BX was 2.9 cm, or 3.01 cm, or any reasonable length for that matter, we could still have used the same “trick” and gotten the same result. So this is a distractor. The teacher who set this question was sneaky, eh? Is it fair? Well, mathematics is not just about arithmetic and calculation. It is also about great ideas like “areas are the same after shifting around (translations and rotations)”. Being able to judge the relevancy of a piece of information is also critical in school, as well as in life in general. This is an example of mathematics in the Singapore curriculum that really makes pupils (and even adult parents and tutors helping them) think! Thinking of a related problem is a powerful heuristic. Sometimes, problems can be solved by thinking of it in another way. With some creativity, you can make the cut! (no pun intended)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is one of the great examples where education is about teaching people how to think for themselves instead of merelyrecalling facts (which has its own place). Considering that repositories for information are now more fluid and accessible, what's left for us (and even challenged by narrow AI) is the ability to synthesize new insights from preexisting concepts. Great post and I'd definitely like to see more of your stuff. Thanks!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @tradersharpe! You have completed some achievement on Steemit and have been rewarded with new badge(s) :
Click on any badge to view your own Board of Honor on SteemitBoard.
For more information about SteemitBoard, click here
If you no longer want to receive notifications, reply to this comment with the word
STOPDownvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post recieved an upvote from minnowpond. If you would like to recieve upvotes from minnowpond on all your posts, simply FOLLOW @minnowpond
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post recieved an upvote from minnowpond. If you would like to recieve upvotes from minnowpond on all your posts, simply FOLLOW @minnowpond
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit