We know the formula for the area of a circle but can we prove it is correct? If you can calculate the area of a triangle you can deduce this formula.
Many proofs for πR² seem to be overly complicated to a student of mathematics. When we use geometry instead of integration, the proof is simpler and intuitively easier to understand. By using isosceles triangles to mimic segments of a circle, we can arrive at our familiar formula.

Triangles Become Segments
Looking at Figure 1, we can see that we are almost there in our attempt to calculate the area of a segment of the circle, and therefore, the whole circle. However, it is obvious that the area of the segment edge cannot be calculated due to the curve of the circle. This edge area may be small, but it is important. The formula that we want to prove accounts for the whole area of the circle.
The answer is to make the triangle thinner. In Figure 2 this thinner triangle is heading in the right direction because the proportion of the segment that is unfilled is smaller. Notice how the height of the triangle is increasing to almost the same length as the radius.
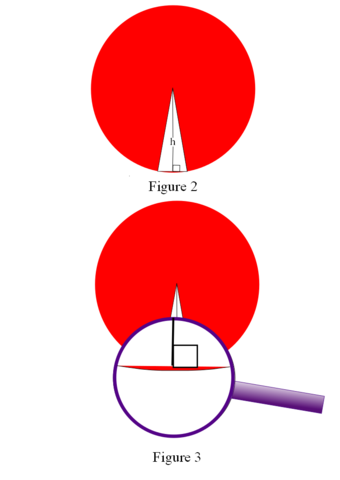
What if we made the triangle really thin, so that it almost disappears. In theory we can make the base of the triangle as small as we want, even down to the width of an atom or a millionth of the width of an atom. We can do this because mathematics is a mental exercise. As the base of the triangle approaches zero, the triangle becomes a perfect segment. In addition, as the base approaches zero, the height of the triangle becomes the radius of the circle.
Infinite Addition
Once we have divided our circle into an infinite number of triangles, we only have to add them together to find the area of the whole circle. “Hold on a minute,“ you may ask, “Won’t that take an infinite amount of time?”
Well, let’s look at the addition sum:
Area of circle = (½ x b1 x h) + (½ x b2 x h) + (½ x b3 x h) + … etc.
We can take the common factors out of every bracket to get:
Area of circle = ½ x h x (b1 + b2 + b3 + … etc).
If you are not sure about this you can prove it for yourself, e.g.:
(5 x 7) + (5 x 6) + (5 x 11) = 120, and is the same as: 5 x (7 + 6 + 11) = 120.
Back to our equation:
Area of circle = ½ x h x (b1 + b2 + b3 + … etc).
Remember the height of these wafer-thin triangles is the same as the radius of the circle, so we can write:
Area of circle = ½ x R x (b1 + b2 + b3 + … etc).
It won’t take us long to add all these infinite bases together, simply because we already know what they make when combined: that is correct, they add up to the circumference of the circle itself.
Therefore, the area of a circle = ½ x R x 2πR.
We have now proved our well known formula:
The Area of a Circle = πR².
I admire the graphics and they are extremely helpful to the explanation. Nice work.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks Kumo,
I use an open source graphics program called Inkscape.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Very nice. The way Archimedes might have explained it. Thank you.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by cheretta from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, theprophet0, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit