Ecuaciones no Lineales y Optimización | 2da Parte

Saludos queridos lectores, bienvenidos nuevamente a mi Blog. En la ciencia, como en la Ingeniería, las ecuaciones no lineales, es un tema de gran interés, ya que las mayoría de los fenómenos físicos o de la vida real, están modelados por ecuaciones no lineales; estos fenómenos naturales por lo general se dicen que están fuera de equilibrio es estos casos y las ecuaciones dependerán de la naturaleza del fenómeno, es decir, discretas o continuas, en cuyos casos se representan por mapeo o ecuaciones diferenciales respectivamente. En esta publicación continuaremos tratando el temea de las Ecuaciones no Lineales y Optimización y en esta oportunidad continuaremos tratando de responder algunos aspectos de como encontrar los ceros a una función, que en muchos casos es parte de la resolución de alguna aplicación real. Espero sigan disfrutando; esta publicación está dirigida a profesionales e investigadores con algunas destrezas en temas de análisis real, cálculo avanzado, entre otros. Al final, les dejare una corta bibliografía, donde podrán consultar algunos tópicos especiales para los interesados. Estoy abierto a sus comentarios y dudas que puedan surgir dentro del tema. Sin perder más tiempo, comencemos.

Podemos decir que el >b>método de bisección, en el cálculo numérico, el un método algorítmico que se utiliza para la búsqueda de raíces o ceros de una función, el mismo consiste en ir dividiendo el intervalo donde se requiere encontrar la raíz, por la mitad y luego por una comprobación seleccionar la mitad que contiene a la raíz.

En el gráfico siguiente podemos apreciar como es el proceso algorítmico descrito anteriormente.

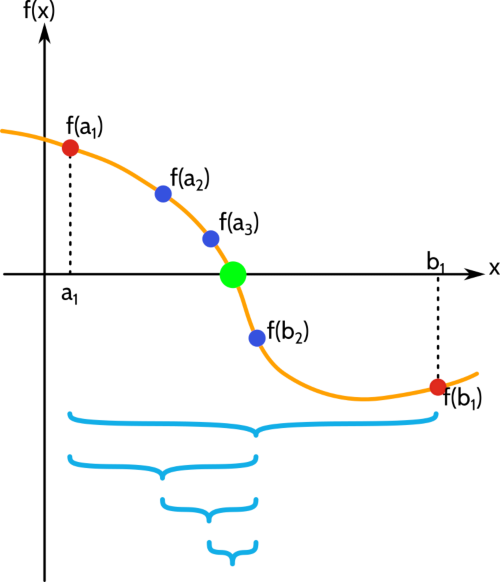
_{Método de Bisección. La imagen fue modificada con Inkscape por @abdulmath. Imagen original}

Ahora bien, describamos más el método:

Supongamos que una función continua f(x) cambia de signo en un intervalo, por lo tanto la misma debe tener al menos una raíz en dicho intervalo. Este hecho, lo que hace es construir una sucesión de intervalos encajados cada vez más pequeños donde cada uno de ellos contiene a una raíz de f(x).

Para ellos, supongamos que f(a)f(b) < 0 y que m = (a+b)/2, es el punto medio del intervalo [a, b]. Así podemos deducir que f(a)f(m) < 0 ó f(m)f(b) < 0. Entonces concluimos lo siguiente en cada uno de los dos casos: si f(a)f(m) < 0 entonces existe una raíz en el subintervalo [a, m], mientras que si f(m)f(b) < 0 implica que existe una raíz en el subintervalo [m, b]. En cualquier caso, nos quedamos con un subintervalo de tamaño la mitad del intervalo inicial. Así, podemos continuar dicho proceso de reducción a la mitad hasta que el intervalo actual sea más pequeño que una epsilon fijado positivo, lo cual podemos apreciar en el script siguiente:

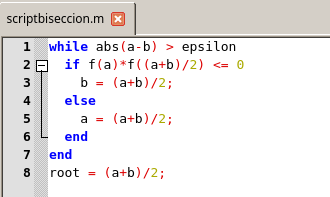
_{Script de implementación del método de bisección. Elaborado en GNU Octave, por @abdulmath.}
Este es un primer script para el método de bisección. Necesitamos optimizarlo, para ello lo primero que debemos tener en cuenta es que el ciclo while nunca puede terminar si el valor de epsilon es más pequeño que el espaciado de los números en la notación de punto flotante entre a y b.

Para ello es necesario modificarlo de la siguiente manera

while abs(a-b) > epsilon + eps*max(abs(a),abs(b))

Esto garantiza que el proceso culmine incluso si el epsilon es demasiado pequeño. Lo segundo que debemos optimizar en la implementación anterior son las evaluaciones de f, ya que se requieren dos dos evaluaciones de la función en cada iteración. Más, sin embargo, con un poco de manipulación, es posible reducir las mismas a una sola evaluación de la función f en cada iteración. Luego, obtenemos el siguiente script optimizado

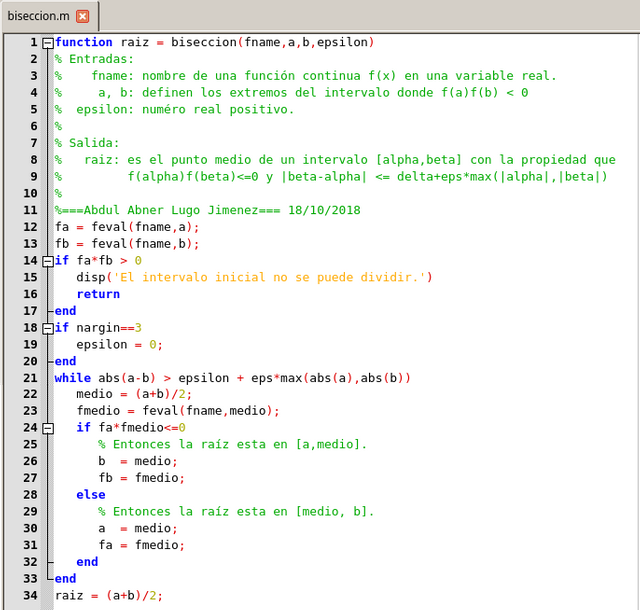
_{Función para el método de bisección. Elaborado en GNU Octave, por @abdulmath.}

Si implementamos la función anterior para encontrar la raíz en el proceso iterativo, debemos destacar que el tiempo que se requiere para encontrar dichas raíces con el método de bisección es proporcional al número de evaluaciones de la función, el resto de las operaciones adicionales a las evaluaciones en la función son insignificantes.

Si [a_k, b_k] es el k-ésimo intervalo del proceso iterativo, entonces

con lo cual se muestra que la convergencia del método está garantizada. Ahora bien, si


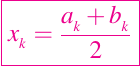
es la k-ésima iteración, entonces existe una raíz x₊ para f(x) con la siguiente propiedad


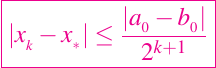
La cota del error se reduce a la mitad en cada paso. Este es un ejemplo de convergencia lineal. En general, la sucesión { x_k } converge a x₊ linealmente si existe una constante c en el intervalo [0, 1) y un entero k₀ tal que


para todo k mayor o igual que k₀.

Para ilustrar cómo es la convergencia lineal, aplicamos el método de bisección a la función f(x) = tan (x/4) - 1 con intervalo inicial [a₀, b₀] = [2, 4]:

k	ak	ak	bk - ak
0	2.00000000000000	4.00000000000000	2.00000000000000
1	3.00000000000000	4.00000000000000	1.00000000000000
2	3.00000000000000	3.50000000000000	0.50000000000000
3	3.00000000000000	3.25000000000000	0.25000000000000
4	3.12500000000000	3.25000000000000	0.12500000000000
5	3.12500000000000	3.18750000000000	0.06250000000000

Como podemos ver el intervalo se va haciendo mas pequeño, y podemos así continuar el proceso

k	ak	ak	bk - ak
43	3.14159265358967	3.14159265358990	0.00000000000023
44	3.14159265358978	3.14159265358990	0.00000000000011
45	3.14159265358978	3.14159265358984	0.00000000000006
46	3.14159265358978	3.14159265358981	0.00000000000003
47	3.14159265358978	3.14159265358980	0.00000000000001

Notemos que se va obteniendo un nuevo dígito de pi cada tres o más iteraciones. Este tipo de obtención es uniforme de dígitos significativos lo cual es una característica distintiva de los métodos que convergen linealmente.

---

---

Supongamos que tenemos el valor de una función f(x) y su derivada f'(x) en x = x_c. La recta tangente

lo podemos considerar como un modelo lineal de la función en este punto.


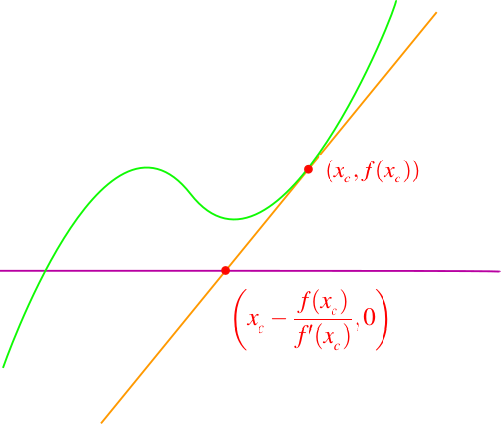
_{Modelando una función no lineal. Elaborada por @abdulmath con Inkscape.}

Una raíz o un cero de la función L_c(x) esta dado por

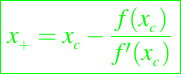
Si L_c(x) es un buen modelo en un rango de valores suficientemente amplio, entonces x₊ debería ser una buena aproximación a una raíz de f. El uso repetido de la fórmula de actualización x₊ define el framework de Newton de la siguiente manera:


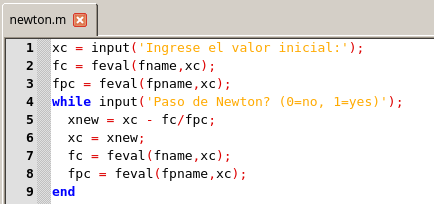
_{Script de Newton. Elaborado con GNU Octave, por @abdulmath.}
Esto supone que fname y fpname son cadenas que albergan respectivamente el nombre de una función y el nombre de su derivada (por ejemplo, fname = 'sin'; fpname = 'cos').

A manera de ilustración, apliquemos el framework de Newton al problema de encontrar un cero de la función f(x) = tan(x/4) - 1:

0	1.00000000000000	2.14159265358979
1	3.79631404657234	0.65472139298255
2	3.25943543617547	0.11784278258568
3	3.14513155420752	0.00353890061772
4	3.14159578639006	0.00000313280027
5	3.14159265359225	0.00000000000245
6	3.14159265358979	0.00000000000000

Esto debe compararse con los 47 pasos del método de bisección requeridos para producir la misma precisión. Aparentemente, después de algunas iteraciones llegamos a una etapa en la que el error es aproximadamente cuadrática en cada iteración. Esto caracteriza los métodos que convergen cuadráticamente. Para una sucesión con esta propiedad, existe un entero k₀ y una constante positiva c tal que

para todo k mayor o igual que k₀. La convergencia cuadrática es una característica muy buscada en el negocio de búsqueda de raíces.

---

---

Queridos amigos y lectores, espero hayan disfrutado de esta segunda entrega de este tan apasionante e interesante tema del cálculo numérico, Ecuaciones no Lineales y Optimización | 1era Parte apoyado con el entorno GNU Octave, en esta oportunidad pudimos estudiar el método clásico para encontrar raíces como lo es el método de bisección, y mostramos las ideas del método de Newton y como este mejora la convergencia de lineal a cuadrática. Espero que el mismo sea de apoyo a ustedes en sus trabajos, o quizás sirva de apoyo para sus hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.

Si desean consultar un poco más del tema pueden usar las siguientes referencias:

• Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
• Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
• Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.

---

Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave, , GIMP e Inkscape.

---

---

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

_{Imagen diseñada con GIMP y elaborada por @abdulmath.}