


En resumen, hasta el momento hemos visto que el método de bisección converge linealmente (ver Ecuaciones no Lineales y Optimización | 1era Parte) mientras que el método de Newton lo hace de forma cuadrática (ver Ecuaciones no Lineales y Optimización | 2da Parte).
Sin embargo, a diferencia del método de bisección, el cual es bastante laborioso, el mismo garantiza la convergencia, grandes cosas pueden salir mal durante la iteración de Newton. No existe garantía de que x+ esté más cerca de una raíz que xc. Después de todo, es producido por un modelo lineal y f puede ser no lineal. Además, un valor pequeño para f'(x+) va en contra de una convergencia rápida. Si la primera derivada es pequeña en la solución, entonces la línea tangente en la que se basa el paso de Newton es casi horizontal y tiene problemas para predecir x+. A continuación mostramos un cuadro donde mostramos el número de iteraciones necesarias para encontrar un a la función f(x) = x2 - a2 con valor inicial t = 2
| a | # de Iteraciones |
|---|---|
| 100 | 5 |
| 10-4 | 18 |
| 10-8 | 31 |
| 10-12 | 43 |
| 0 | 50 |
Note que f'(x+) = 2a y que la tasa de convergencia pasa de ser muy cuadrática a ser esencialmente lineal y disminuye de 1 a 0.
Pero cosas aún peores pueden suceder debido a los valores pequeños de la derivada. Si f'(xc) es pequeño en relación a f(xc), entonces el paso de Newton puede llevarnos a una región lejos de donde esta ubicada una raíz.
El ejemplo clásico de esto es la función f(x) = arctan(x). Ya que, f'(x) = 1/(1 + x2), la actualización de Newton tiene la forma
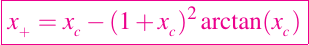
Se puede mostrar que si |xc| > 1.3917, entonces |x+| > |xc|. Esto implica que la iteración diverge para valores iniciales fuera de [-1.3917, 1.3917].
Para garantizar la convergencia de cualquier valor inicial en una vecindad de alguna raíz, se puede demostrar que f no puede ser demasiado no lineal y que f' debe estar acotada fuera del cero. El siguiente teorema muestra lo que decimos.

Supongamos que f(x) y f'(x) se definen en un intervalo I de la forma siguiente

donde
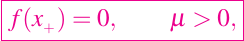
y existen constantes positivas rho y delta de tal manera que
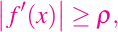 para todo x en I.
para todo x en I.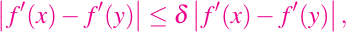 para todos los valores de x, e y en el intervalo I.
para todos los valores de x, e y en el intervalo I.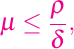
si xc esta en el intervalo I, entonces
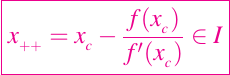
y
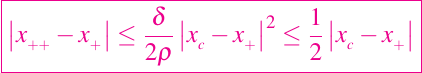
Por lo tanto, para cualquier xc en el intervalo I, un paso de Newton más que la mitad de la distancia a x+, garantiza así la convergencia para cualquier valor de partida en I y la tasa de convergencia es cuadrática.
El teorema muestra que si (1) la derivada f' no cambia de signo en un entorno de x+, (2) f no es demasiado no lineal, y (3) la iteración de Newton comienza lo suficientemente cerca de x+, entonces la convergencia está garantizada a una tasa cuadrática.
Para todas las funciones excepto las más simples, puede ser imposible verificar que se aplican las condiciones del teorema. Un resolvedor de ecuaciones no lineales de propósito general, basado en Newton, requiere un empaque cuidadoso para que sea útil en la práctica. A diferencia de la bisección, donde la longitud actual del intervalo limita el error, tenemos que confiar en la heurística para concluir que una iteración es aceptable como raíz calculada.
Una posibilidad es salir cuando |x++ - xc| sea lo suficientemente pequeño. Después de todo, si lim xk = x+, entonces lim |xk+1 -xk| = 0. Pero lo contrario no necesariamente sigue. Si f(x) = tan(x) y xc = (pi)/2 - 10-5, entonces |x++ -xc| es aproximadamente 10-5 aunque la raíz más cercana esté en x = 0. Alternativamente, podríamos terminar tan pronto como |f(xc)| sea pequeña. Pero esto no significa que xc esté cerca de una raíz. Por ejemplo, si f(x) = (x - 1)10, entonces xc = 1.1 hace a valor de f muy pequeño aunque esté relativamente lejos de la raíz x+ = 1.


Las dificultades que se acaban de discutir pueden ser manejadas con éxito combinando las ideas de Newton y Bisección de una manera que capture las mejores características de cada método. Al principio en el primer paso asumimos que tenemos un intervalo de cerrado [a, b] y que xc es igual a uno de los puntos finales. Si
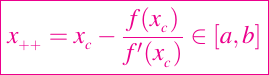
entonces procedemos con cualquiera de los intervalos [a, x++] o [x++, b]. El nuevo xc es igual a x++. Si el paso de Newton nos lleva fuera de [a, b], entonces tomamos un paso de bisección ajustando el nuevo xcc a (a + b)/2. Para comprobar si el paso de Newton se mantiene en [a, b], usamos la siguiente función
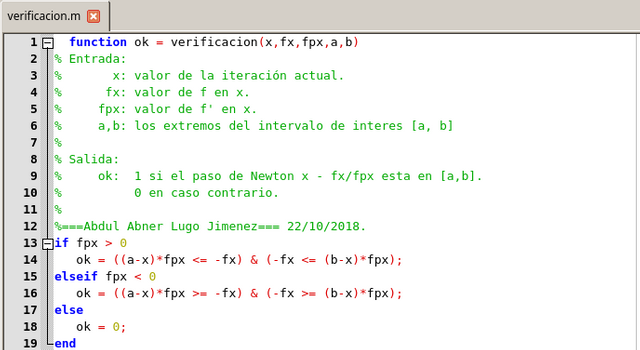
Función de Verificación. Elaborado en GNU Octave, por @abdulmath.
Para garantizar la finalización, detenemos la iteración si se cumple alguna de las siguientes tres condiciones:
- La longitud del intervalo de dividido actual es menor que
tolx, una tolerancia no negativa específica. Esto asegura que la raíz calculada está dentro de la tolerancia de una raíz verdadera. Esto no garantiza que f sea pequeña. Por ejemplo, si f(x) = (x - 1)0.1, entonces xc = 1.0000000001 está muy cerca de la raíz x+ = 1, pero f(xc) no es particularmente pequeño. - El valor absoluto de f(xc) es menor o igual que
tolf, una tolerancia no negativa especificada. Esto no significa que xc esté cerca de una raíz verdadera. Por ejemplo, si f(x) = (x - 1)10, entonces xc = 1.1 hace que f sea muy pequeño a pesar de que está relativamente lejos de la raíz x+ = 1. - El número de evaluaciones de f excede un entero positivo especificado
nEvalsMax. Esto significa que no se cumple ninguna de las dos condiciones anteriores.
Al juntarlo todo, obtenemos la siguiente función del método de Newton generalizada.
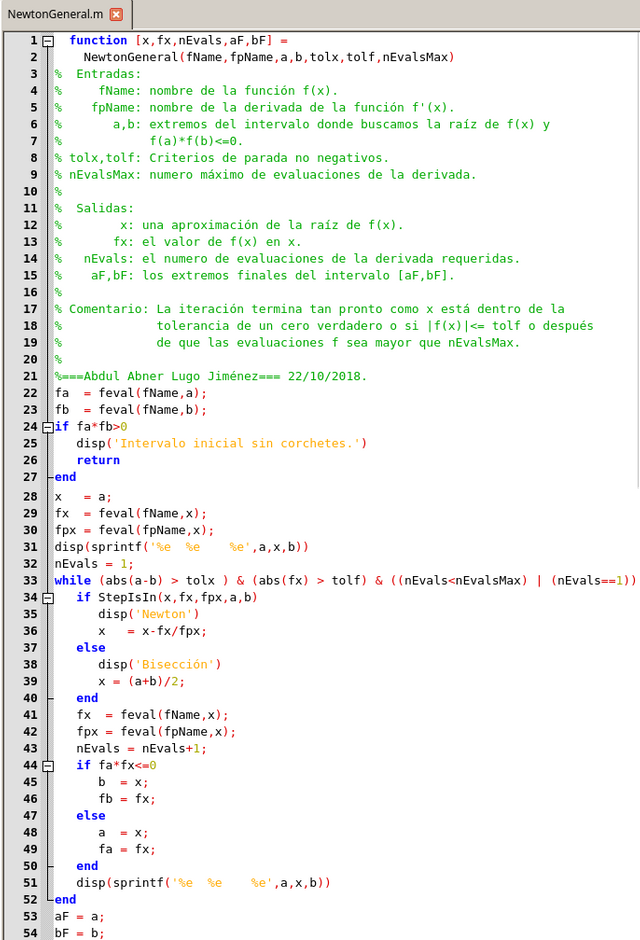
Función de Newton Generalizada. Elaborado en GNU Octave, por @abdulmath.
En una situación típica, se toman una serie de pasos de bisección antes de iniciar las iteraciones de Newton. Por ejemplo, si intentamos encontrar un cero de f(x) = sin(x) con el intervalo inicial como sigue:
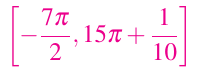
| Pasos | a | x | b |
|---|---|---|---|
| Inicio | -10.995574287564276 | -10.995574287564276 | 47.223889803846895 |
| Bisección | -10.995574287564276 | 18.114157758141310 | 18.114157758141310 |
| Bisección | -10.995574287564276 | 3.559291735288517 | 3.559291735288517 |
| Newton | 3.115476144648328 | 3.115476144648328 | 3.559291735288517 |
| Newton | 3.115476144648328 | 3.141598592990409 | 3.141598592990409 |
| Newton | 3.141592653589793 | 3.141592653589793 | 3.141598592990409 |

Queridos amigos y lectores, espero hayan disfrutado de esta segunda entrega de este tan apasionante e interesante tema del cálculo numérico, Ecuaciones no Lineales y Optimización | 3era Parte apoyado con el entorno GNU Octave, en esta oportunidad pudimos estudiar algunas consideraciones sobre la convergencia de los métodos de bisección y Newton, así como construimos una generalización del método de Newton. Espero que el mismo sea de apoyo a ustedes en sus trabajos, o quizás sirva de apoyo para sus hijos, nietos, sobrinos o amigos que quieran aprender un poco más del maravilloso mundo de las matemáticas y la programación. No olviden dejar sus comentarios. Saludos y nos leemos pronto.
Si desean consultar un poco más del tema pueden usar las siguientes referencias:
- Demidovich, B. P., and I. A. Maron. Computational Mathematics Mir, Moscow, 1976.
- Björck, Åke. Numerical methods in matrix computations. Vol. 59. Cham: Springer, 2015.
- Burden, Richard L., and J. Douglas Faires. Numerical analysis. Ninth Edition. Cengage Learning. 2011.
Las imágenes, separadores y las ecuaciones fueron creadas y editadas por @abdulmath usando software libre, GNU Octave,  , GIMP e Inkscape.
, GIMP e Inkscape.

@SteemSTEM es un proyecto comunitario con el objetivo de promover y apoyar la Ciencia, la Tecnología, la Ingeniería y las Matemáticas en la blockchain Steem. @Stem-espanol es parte de esta comunidad, si desea apoyar el proyecto, puedes contribuir con contenido en español en las áreas de Ciencia, Tecnología, Ingeniería y Matemáticas, utilizando las etiquetas #steemstem y #stem-espanol.

It's graceful not just strong!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you very much for your comment. Best regards.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Bastante técnicos sus posts, Dr. AbdulMath, Esperemos en el futuro más matemáticos con su línea de investigación se unan a la comunidad y se nutran en sus discusiones. Mis temas favoritos son cuando se plantean modelos matemáticos, pero en especial cuanto más cerca a lo concreto estén y sean asequibles al público no necesariamente especialista. Encomio su labor. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by abdulmath from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @abdulmath! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
Click here to view your Board of Honor
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ticket Nº22
* Recuerda el número de tu ticket porque estás participando automáticamente en un sorteo especial que se anunciará el ganador el día de la fiesta.
Pd: Si tienes un amigo que desee ir, dile que se pase por La invitación de Reveur y reclame su ticket.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias por la invitación, allí estaré en la festa.
Un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit