Transportation of Fluid and Solid Matter:

A Pipeline
It is often said that the most important invention in the history of Mankind is the wheel. This is due to the wheel being a form of transportation medium that allowed the world to expand and grow into the advanced societies that we are. Nowadays when we hear the word transport, we immediately refer to means of mobile cars, trains or even ships. But what about a pipe? Had transportation through pipes not being possible, many products we have today would not be possible to have, as the materials used to make these products would have experienced pipe transportation within a chemical engineering site. This post is to elaborate on a Fixed Bed Reactor, which is the common drop off zone of the fluid within a pipe (before it is released into another pipe once more) in Chemical Engineering and to elaborate on the calculations involved to ensure that we are using the correct specified pipelines/reactors.
A fixed bed, also known as a packed bed, is a reactor that contains stagnant catalyst pellets, and are renowned for having an extremely important role in the chemical engineering society. Although these advanced pieces of equipment may have a rather simple design, they have an extensive range of applications such as, adsorption, drying, collection of dust, filtration as well as facilitating other reactors including catalytic and non-catalytic reactors. The main operating factor that affects a Fixed Bed Reactor is the pressure drop that occurs through the bed of solids in this reactor.
You may be wondering what a pressure drop is, and you may think that this is some really intricate form of calculation, am I right? Surprisingly, it is a rather simple concept. A pressure drop is a measure of the amount of pressure that is reduced by a system due to a process. In the case of a Fixed Bed Reactor, the pressure drops acts across the packed beds.
In the world of fluid mechanics, there are 2 very important flows that have individual characteristics that affect our choice of pipelines. The calculations performed will help us obtain the pressure drops that occurs across the beds of the reactor and will therefore facilitate in our overall evaluation of the reactors. These flows are regarded as Laminar or Turbulent Flow. Laminar flow, also referred to as streamline flow, is the flowing of fluid that contained no disruptions in adjacent layers of a flowing fluid, while Turbulent flow is the opposite of Laminar flow.
Laminar Flow
With regard to Laminar Flow, a relationship was observed in 1856 which stated that the pressure gradient within the Fixed Bed was directly proportional to that of the liquids velocity.
(- dp)/L ∝ 𝑢
- '𝑢' is the fluids velocity through the bed
- '- dp' is regarded as the frictional pressure drop that occurs across a bed of depht L
NOTE: fluid velocity can be calculated by dividing the volumetric flow rate of the fluid by the cross-sectional area of the bed.
𝑢 = Q/Ac
The relationship obtained was used by scientists to create an equation referred to as The Hagen-Poiseuille Equation. It is used to analyze laminar fluid flow through the packed bed that contain solid particles.
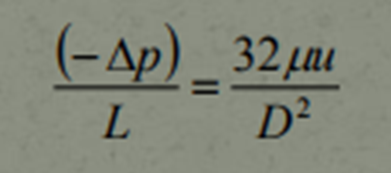
- D is referred to as the diameter of the Fixed Bed
- The Symbol between "32" and "𝑢" is referred to as "Mu" (a Greek symbol) that represents Dynamic Viscosity.
- L is the characteristic lenght of the pipe.
Another equation that was produced later on in 1937 from the identified relationship is referred to as The Carman-Kozeny Equation. It has the same purpose to that of the Hagen-Poiseuille Equation but the only noticeable difference is that this equation uses different variables to assess the flow.
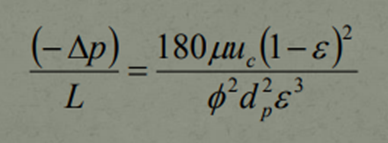
- Sigma (which the only cubed term in the denomonator) is referred to as the porosity of the Fixed Bed.
- Phi (the first term in the denomonator) is referred to sphericity which is the measure of how spherical an object is.
As mentioned, sphericity is a parameter of any object and is used to analyse to what extent any object is spherical. It is governed by the following equation,
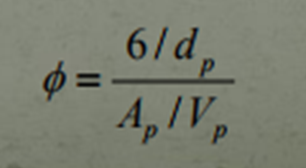
NOTE: all variables have the subscript "p" as this indicates it is reference to the particle of choice.
- d - the diameter of an individual particle
- A - the surface area of an individual particle
- V - the volume of an individual particle
It can be noted that for a sphere, phi would be 1.
Also, the numerator of the equation is related to the ratio between the surface area and volume of a sphere while the denominator is the ratio related to that of the related object. It can therefore also be deduced that for any non-spherical object, the surface area of the particle will be greater than the volume of the particle, (Ap > Vp).
Turbulent Flow
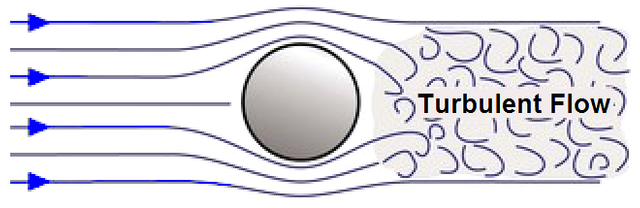
Transition from Laminar Flow to Turbulent Flow
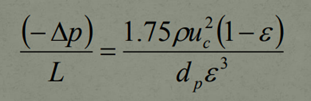
- ρ is referred to as the fluids density
General Equation
In 1952, an equation known as The General Equation was derived. Referred to as The Ergun Equation, this equation is used to assess fluid flow when the type of flow is unidentifiable, that is, can not be recognised to be either laminar nor turbulent.
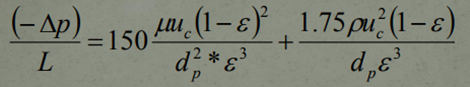
It is important to note that this equation contains pressure gradients for both Laminar as well as Turbulent Flow. Under Laminar fluid flow, the first term will dominate and it can be noted that this term is almost identical to The Carman-Kozeny Equation, except for the fact that the constant value employed here is 150 rather than 180. The reason for the change is to account for any Turbulent flow that may be present at the time as well as to account for any changes in particle size due to the mixture of these 2 flows.
Reynolds Number
Considered to be one of the most important dimensionless numbers in engineering, the Reynolds Number is used quite often in fluid mechanics to identify the type of flow present, based on certain known data of the flow. The results of the equation will fall into 3 groups, which will allocate the type of flow present to that specific fluid. The Reynolds Number Equation is,
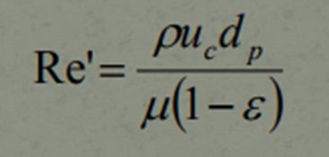
If Re’ < 10, it indicates that the flow is strictly Laminar.
If Re’ > 2000, it indicates that the flow is strictly Turbulent.
If 10 < Re’ < 2000, it indicates that the flow is Intermediate, that is, between Laminar and Turbulent.
Friction Factor Correlations
In the engineering world, working with large equations in industry is often very time consuming as well as more likely to produce errors in calculations. As much as engineers and scientists are considered to be highly intellectual, we must remember that they are also human just like us and are likely to err. In order to prevent such events from occurring, a method of derivation was produced, and this yielded a new way to express a pressure drop in a much-simplified manner. This new equation is referred to as The General Friction Factor Correlation and it is derived from the Ergun Equation (as aforementioned):
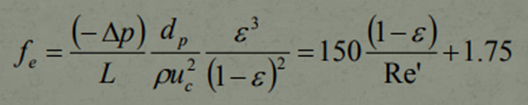
Laminar or Turbulent Flow: If the type of flow is known, the above equation simplifies even further.
f = 150/(Re’) , if the flow is Laminar
f = 1.75 , if the flow is Turbulent
NOTE: All above equations are under the assumption that the particles being used are spherical particles
Non-Spherical Particles
As mentioned in the note before, all equations were used under the assumption that the particle of choice were completely spherical. But what happens when we encounter particles that are non-spherical? Do we just abandon the thought and hope that all particles are spherical? Of course not. To accommodate for these non-spherical entities, a substitution of variables were introduced: d ( sv ) for d ( p ) . d ( sv ) is the diameter of a sphere that has the same surface area to object volume ratio as the non-spherical object. In other words, the non-spherical object is “replaced” by a spherical object of similar properties to assist in calculations and fundamental theories.
The Ergun Equations will become,
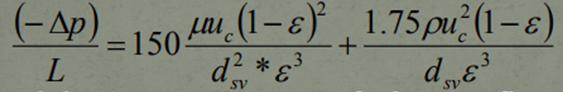
And the Carman-Kozeny Equation (Laminar Flow) becomes,
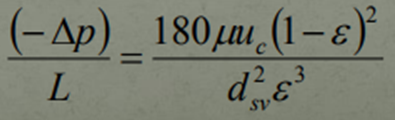
This brings us to the end of fluid flow through a Fixed Bed Reactor. In posts to follow, I was include fluid flow fundamentals which are essentially filtration fundamentals amalgamated with filtration equipment and the filtration cycle.

Particle moving through a flowing Liquid
Images are linked to their sources in their description
The End
References:
[1]https://en.wikipedia.org/wiki/Pipe_flow
[2] Unit Operations of Chemical Engineering by McCabe W.L., Smit J.C. and Harriot P (McGrawHill, 7th Edition, 2005)
[3]https://www.lmnoeng.com/Pressure/PressureDrop.php
[4]https://www.pipeflow.com/pipe-pressure-drop-calculations
[5] Coulson and Richardson's Chemical Engineering. Vol. 2, Oxford, ButterworthHeinemann by RICHARDSON, J. F., HARKER, J. H., BACKHURST, J. R., & COULSON, J. M. (2002).
[6]https://en.wikipedia.org/wiki/List_of_equations_in_fluid_mechanics

Thank you for your post. :) I have voted for you: 🎁! To call me just write @contentvoter in a comment.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you. I really appreciate it :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Nice post! I heard about SkyWay, some scientist trying to improve our transport technology. Maybe we're in new Era of transport!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Most definitly. Our method of survival evolve daily and with the advancements that we experience, we are sure to uncover something amazing!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Yap! Future is bright I hope so :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
What an intricate post and respect to citing references; good on you. Are you an engineer? Any generalized thoughts on pipelines in general and transportation of natural gas?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I hopd to be one day :) regarding the current pipe systems , our lessened reliance on heat due to insulation methods in and around the pipe are an extreme advantage for flowing fluids. There should, however, be a methid of coating to help the lifespan of these pipe, to prevent cost of equipment as well as quality of fluids.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Being A SteemStem Member
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit