Hello friends of physics, today I want to continue sharing with you all different types of experiments that I do during my advanced optics laboratory subject in my undergraduate career at university, then I will talk about spectrometry.
It is an instrumental technique widely used by physicists and chemists to determine the qualitative and quantitative composition of a sample, using patterns or spectra known from other samples. In this investigation it is of interest only the emission spectrometry, by means of this we will identify three different gases unknown at first instance, from the observation of its spectral lines obtained in the spectrometer, we will also determine the rydberg constant of a certain spectrum using the balmer series analysis.

Figure 1. Spectral line.
thoughtco
Spectroscopy was discovered in the 17th century by Newton, who discovered that white light passing through a glass prism breaks down into light with rainbow colors.
In the seventeenth and nineteenth centuries the prism was used for the decomposition of light with slits and telescopic lenses with which a more powerful tool was obtained to examine the light coming from different sources.
Through the spectroscope developed in century XVII was discovered that the spectrum of sunlight was divided by a series of dark lines; on the other hand the light generated in the laboratory by the heating of gases, metals and salts showed a series of narrow, colored and bright lines on a dark background. Therefore the idea of using these spectra as a fingerprint of the observed elements arose.
Emission spectrometry is a technique that consists of analyzing wavelengths of photons emitted by atoms or molecules during their transition from an excited state to a state of lower energy. Each element emits a characteristic set of discrete wavelengths depending on its electronic structure. By observing these wavelengths, elemental composition of the sample can be determined.
The most commonly used way to obtain this light emission is by means of heating. Thus this beam is directed towards the interior of the spectrometer, whose function is to diffract this by means of a grid or to refract it if it is a prism, obtaining measurable spectral lines or bands projected on a graduated scale.
A common spectrometer is composed of three fundamental elements:
Collimator: this is a small slit used to narrow and align the beam of light in order to correctly address it towards the diffracting element.
Diffracting element: it is the one that is in charge of doubling the beam and dividing it forming a spectrum. This function is fulfilled by the steering grid or the prism inside the spectrometer.
Ocular: through this the spectral lines resulting from the beam diffraction are observed to measure the wavelength of each.
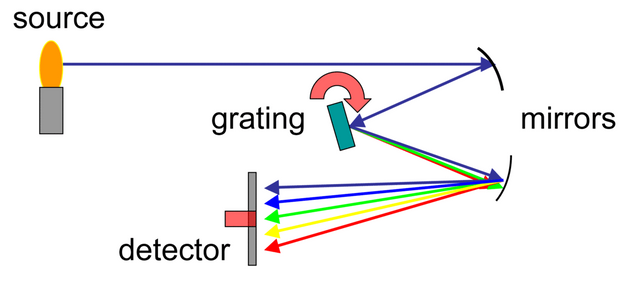
Figure 2. Composition of the spectrometer.
Wikipedia
For this study, a spectrometer with a diffraction grating as a diffraction element was used.
During the nineteenth century, a notable interest in this type of phenomena arose, one of the outstanding scientists was Johann Balmer, who devised a mathematical model by which the characteristic wavelengths of the spectral lines of hydrogen could be obtained and similar elements. Later Johannes Rydberg improved this model by making it dependent on the wave number instead of its length, to this was added a constant value which bears its name as:
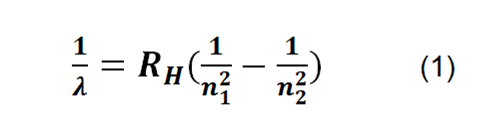
Where λ is the wavelength, R_H is the rydberg constant, and n_1 and n_2 are the values representing the orbital levels of the atom, which determine the series to be used, for the present study the so-called balmer series .
To calculate the corresponding wavelengths by the expression:

Where λ is the wavelength; d the distance between the lines of the diffraction grid (d = 1.66 x10-3 for the grid of 600 lines / mm, for example); θ is the diffraction angle; and m is the order of the diffraction spectrum under observation.
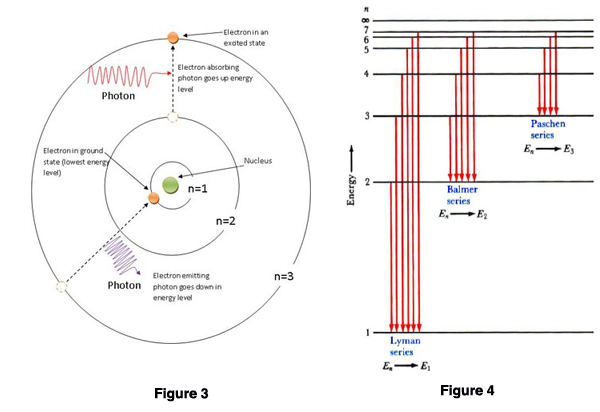
Figure 3. Spectral emission.
Chemskills
To perform this experiment we used the spectrometer with graduated diffraction grating, a lens with a resolution of 7500 lines / in and a scale graded at 10 ^ (- 5) cm, 15000 lineas7pulg. As well as a 5000V source that generates 0.18 Amp for the determination of unknown gases, 3 gas container tubes, which we will analyze in detail and observe its spectral lines and a variable resistance fixed to 750 Ω.
Next we will identify the 3 different gases, for this the variable resistance is connected between the source and one of the electrodes on which the study tube is fixed, the latter is located in front of the collimator of the spectrometer. To calibrate this equipment is made use of a tube containing mercury, this gas is used to have spectral lines very simple and easy to visualize, with knowledge of its characteristic wavelengths emitted, it is necessary to adjust the scale of the spectrometer, once calibrated we proceed to study the samples of the other 3 gases where we will observe their wavelengths and compare it with the theoretical studies and thus to be able to identify what type of gas we obtained.
Calibration of the spectrometer:
- Connect the variable resistor between the source and one of the electrodes on which the mercury tube is attached, which must be placed in front of the spectrometer collimator.

Figure 4. Model of spectrometer used in the laboratory of optics in the University of Zulia "modified original image".
Fisica.ur
Adjust the spectrometer scale.
For each lamp to be placed the spectrometer must be calibrated before taking any measurement.
Study of the unknown source.
Because the tubes with the gases are of very low intensity it is recommended to place each tube as close as possible to the entrance grid of the collimator of the apparatus.
Place the supplied emission source one by one.
The wavelengths of the diffracted beams of each gas are recorded.
With the above information, a comparative study between these experimental values and the theoretical values (obtained through the use of appropriate software, for example, AtomicSpectra.
The data obtained are collected in a table designed for this purpose.
We use mercury as an element to be able to calibrate the spectrometer, which shows in table 1 the wavelengths corresponding to this gas.
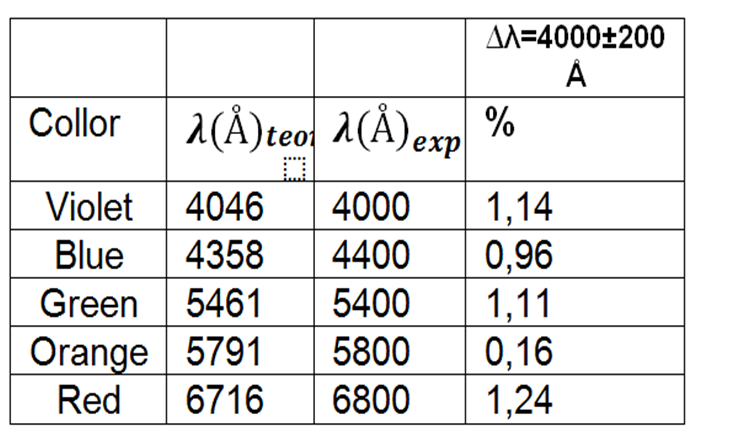
Table 1. Wavelengths of the mercury gas emission spectrum used to calibrate the instrument.
The results obtained during the experiment that consisted in identifying the gas in the tubes were the following:
For the first gas the following table is shown:
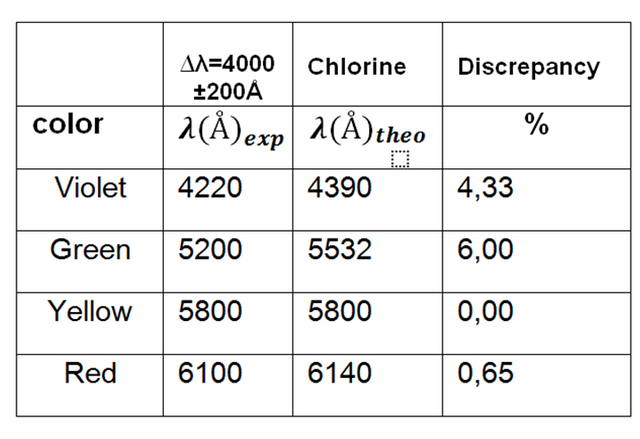
Table 2. Values of observed wavelengths for tube 1.
Analyzing the gas through the AtomicSpectra application we observe and compare the emission spectrum and say that the gas contained in the tube is chlorine.
For the second gas the following table is shown:
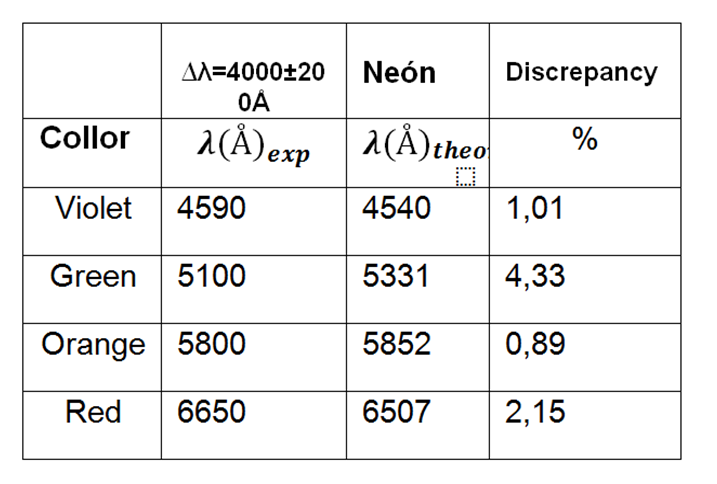
Table 3. Values of observed wavelengths for tube 2.
Through the AtomicSpectra we compare the results and identify the gas being this Neon.
For the third gas the following table is shown:
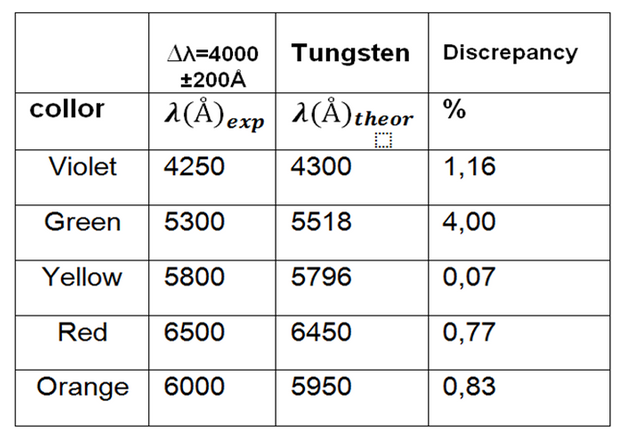
Table 4. Observed length values for tube 3.
Using the AtomicSpectra to buy the results we identify the gas as the tungsten.
Now in the second part of this experiment we will calculate the rydberg constant of the mercury tube, with the results obtained experimentally from its color spectra, this constant has a theoretical value of R = 1,097x 10 ^ 7 m ^ (-1) , which we will compare and obtain its % discrepancy.
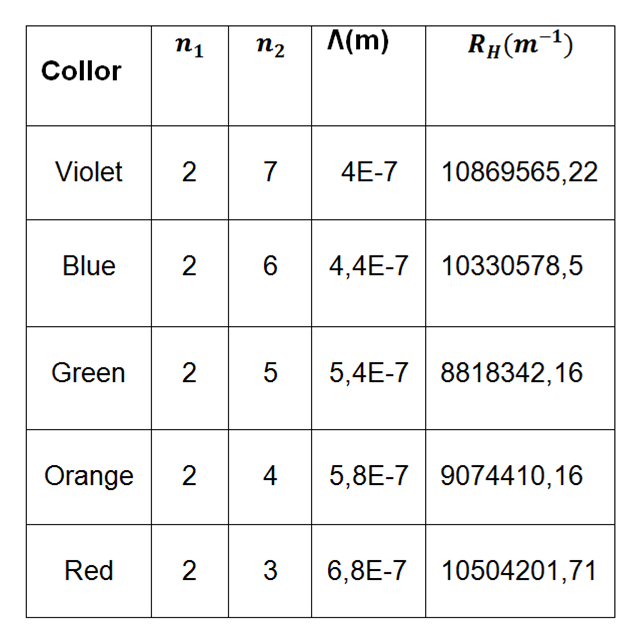
Table 5. Shows the wavelength values taken for the calculation of equation (1).
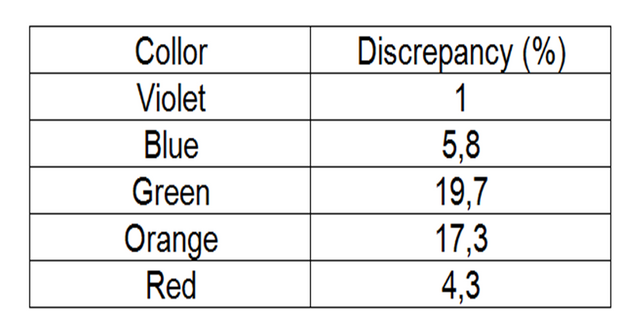
Table 6. Discrepancy of mercury spectrum.
From Table 5 the error calculation was obtained:
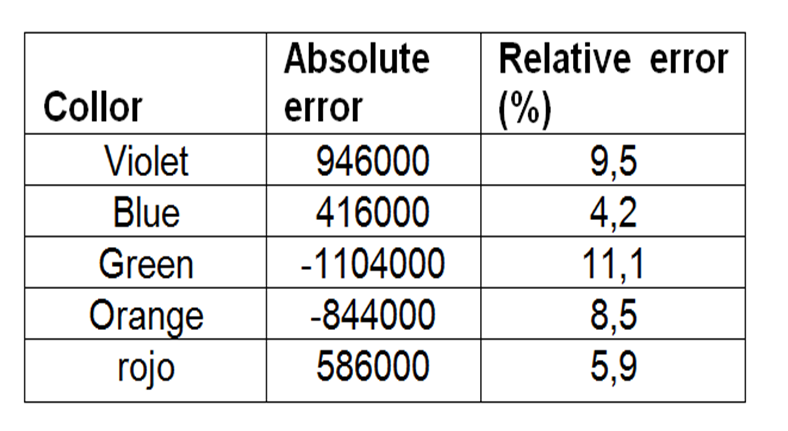
Table 7. Shows the calculation of errors of the mercury spectra obtained with equation (1).
In the first part of this experiment we can conclude that the objective was achieved satisfactorily since we were able to visualize through the tubes of the different gases the wavelengths corresponding to each emission spectrum, with a margin of error or discrepancy of 0.92 for mercury, 2.7 for chlorine, 2.1 for neon and 1.37 for tungsten.
In the second part it was also possible to calculate the rydberg constant of the mercury gas with a 9.6% discrepancy.
We must take into account that these experiments were performed with an input error of 5% for which the errors were high, in addition we must consider that also the brand or type of spectrometer is very important to be able to visualize the spectral lines more clearly and its wavelengths are accurate, the grid does not have adequate resolving power to visualize well the spectral lines. Another point to take into consideration are the random errors that greatly influence the performance of this experiment.
REFERENCES
Robert Eisberg and Robert Resnick. "QUANTUM PHYSICS". 2011. Editorial Limusa Wiley. P 126-130.
Mark Kness, 2002. Application AtomicSpectra. V1.0 Copyright 2002.
"EXPERIMENTAL TECHNIQUES SCREENINGS III" (Quantum Physics Section) COURSE.2006 / 2007. https://www.usc.es/gir/docencia_files/te3/guiones.pdf