FLUID PRESSURE: FLOATING, FLOWING AND FLYING.

The movement of air over a curved surface produces unexpected forces that allow objects heavier than air to fly. These forces can be explained using Newton’s laws, and can also be related to the way water flows, in pipes and rivers for example.

Newton’s laws of motion are best expressed for fluids in a statement of the Swiss mathematician Daniel Bernoulli (1700-1782) and known as Bernoulli’s principle. Other important ideas the I will mention in this section of the chapter are fluid pressure, thrust, and viscosity (the name for the internal friction of a fluid). I will consider hydrostatics and hydraulics, which deal with the behaviour and uses of liquids under pressure. I will also deal with the behaviour of fluids in response to forces. This behaviour is best explained using the kinetic theory of matter, which will be explained in another post of mine.

So, let’s start with Pressure…….

Pressure is defined as the force exerted on a surface per unit area

Pressure = force / area

P= F/A

Pressure is a scalar quantity with units of newtons per square metre. The unit of pressure has a special name, the pascal (Pa): 1 pascal – 1 Nm^-2. This is a very tiny quantity – ordinary pressures are several thousand pascals: the pressure of the atmosphere for example is 10⁵ Pa.

^{A Ski reduces the pressure on snow. Pixabay}

The figure above shows a simple example of the same force producing different pressures, due to the weight of a skier with and without skis. The large area of the ski ‘spreads the load’, and the weight of the body is more easily supported by the soft snow.

PRESSURE IN LIQUIDS

Pressure in a liquid has special features that are written below. Theory and experiment show that in a liquid:

• Pressure increases with depth.
• At a given point in a liquid, the pressure acts equally in all directions.
• A liquid can transmit a pressure exerted on it at one place so that it acts at some other place.

To say that a liquid ‘finds its own level’ means that in any connected system the level of the liquid must everywhere be the same. If it isn’t at any time then the difference in pressure will cause the liquid to move until the difference disappears. This is why a small clear tube outside a fuel tank can be used to show the level of the fuel inside.

Hydrostatic pressure

The pressure at the bottom of a cylindrical jar of liquid is caused by the weight of the liquid and of the atmosphere above the liquid surface. We now consider the pressure P due to the liquid alone,

The liquid has density ρ. The mass of water in the cylinder is thus:

m = volume × density = Ahρ

The weight of this mass is mg = Ahρg and is a force acting over the area A. Thus the pressure P (force per unit area) caused by the liquid on the base of the cylinder is:

P = mg / A = hρg

Any object placed at this depth will be acted upon by this pressure. If you made a small hole in the side of the cylinder, water would be forced out sideways. It is perhaps surprising that this pressure acts in all directions, not just downwards as happens with, say, skis used in the previous example. The force due to fluid pressure is usually called thrust.

thrust = pressure × area

F = PA

Higher up we might expect that the pressure is less. For example, at a depth y, the pressure should be simply, P = yρg

This is the basic relation in the science of hydrostatics, and is a simple formula that works for liquids which have a constant density. Simple experiments confirm that pressure increases with depth in a fluid and also that pressure acts in all directions. (Gases under pressure are compressed so that the density increases. This complication will be dealt with later.)

MEASURING PRESSURE IN FLUIDS

The simple manometer is being used to measure the pressure of a gas supply. The excess pressure of the gas supply compared with the pressure of the atmosphere is balancing the pressure exerted by the column water. The pressure exerted by the liquid column, hρg, equals the excess pressure of the gas supply.

A barometer is used to measure atmospheric pressure. The original barometers used a column of mercury. Air pressure acts on the surface of the mercury in the dish. This pressure is transmitted through the liquid and produces a thrust, acting upwards at the base of the mercury column, which exactly balances the weight of the column. The space above the column is (almost) a vacuum, created as the mercury column fell to its balancing level of about 76 cm above the surface of the mercury in the dish. The atmospheric pressure is given by hρg where ρ is the density of mercury.(Remember that this pressure is independent of the area of the dish.)

For accurate measurements using a mercury barometer, a correction has to be made for the liquid’s variation in density with temperature, and h has to be measured with great care. Barometers play an important part in weather forecasting: blocks of warm (usually damp) air and cold dry air have different densities, causing different atmospheric pressures at ground level. These pressure changes appear some distance ahead of the associated weather systems.

^{Modern aneroid barometer. Public Domain}

A cheaper instrument for measuring atmospheric pressure is an aneroid (liquid-free) barometer. It has a partially evacuated metal box with a corrugated shape that is kept from collapsing under the pressure of the atmosphere by a strong spring. Changes in atmospheric pressure cause small movements in the surface of the box. These movements are amplified mechanically or electronically for display. Aneroid barometers have to be calibrated from time to time against the more direct measurements made by a mercury barometer. The aneroid principle is also used in an altimeter, since air pressure varies with height.

REASON WHY SHIPS FLOAT: ARCHIMEDES’ PRINCIPLE

Like many people, the Greek scientist and mathematician Archimedes of Syracuse (about 287 to 212 BC), had one of his best ideas in the bath – or so the fable tells us. But wherever he got the idea, Archimedes was the first scientist to realize the significance of the everyday event of the water level rising when you get into a bath. He linked this effect to a problem that he had been given to solve.

^{A floating ship's weight Fp and its buoyancy Fa must be equal in size. Italian Wikipedia, Public Domain}

It was suspected that a royal crown was made of a silver-gold alloy, and not the pure gold supplied to the jeweller who made it. The crown’s density would give Archimedes the answer. He could weigh the crown, but how could he measure its volume? Then he realized that the volume of the crown would equal the volume of water it displaced. Archimedes also considered an object that floated either because it was hollow or because it was less dense than water. He stated that the displaced water would exert an upward force on the object. These ideas are brought together in Archimedes’ principle, which is now stated thus:

When a body is wholly or partly immersed in a fluid it experiences an upward force (upthrust) equal to the weight of the fluid displaced. The effect is due to fluid pressure.

A closer look at Archimedes’ Principle

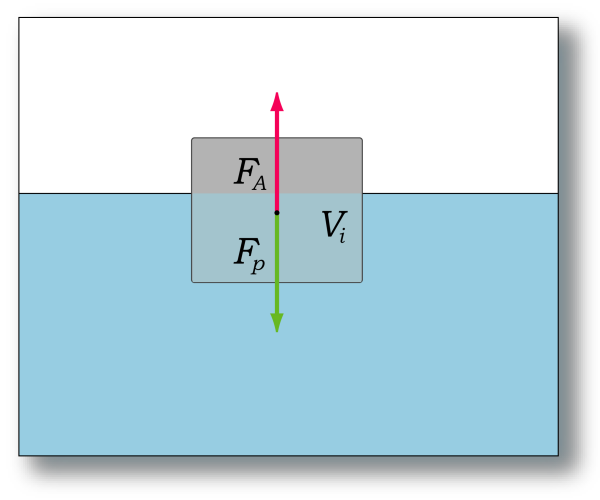
Consider a block of material (assumed regular for the sake of simplicity) floating in a liquid as shown below.

^{An image drawn by me}

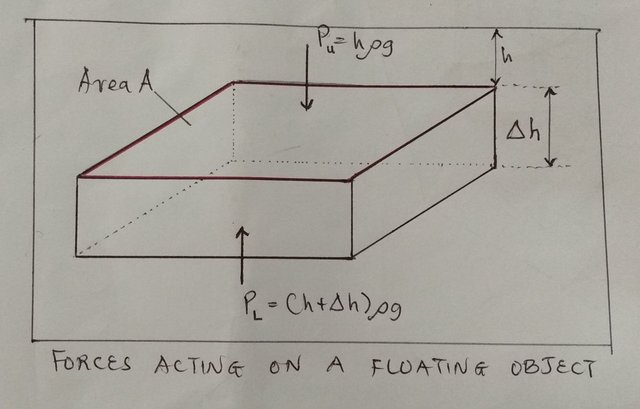
The pressure on its upper surface, P_U is hρg, where ρ is the density of the fluid. This pressure acts vertically on the surface and presses down with a force (thrust) of Ahρg.

The pressure on the lower surface is P_L (h + Δh)ρg and acts upwards with a thrust A(h + Δh)pg. The thrusts on the vertical sides cancel out.

The net thrust on the block is thus upwards and is AΔhpg. But AΔh is the volume (V) of the block and so the expression for the upthrust simplifies to Vρg, which is, of course, the weight of the fluid displaced.

Whether the block sinks or floats depends on its own weight W. If W > Vρg it will sink. If the block is of density ρ_B , its weight is Vρ_Bg, so the condition for sinking is simply ρ_B > ρ. If ρ_B is less than ρ, the block has a net upward force and will rise until it displaces just enough of the fluid for the upthrust to equal its weight.

EXAMPLE

A block of iroko wood has a mass of 200 kg and a density of 570 kgm^-3. What fraction of the wood will be under the surface when the block is floating in water (density 1000 kg m3)?

Answer: The wood will float when it displaces a weight of water equal to its own weight, which is equivalent to saying that the wood and the displaced water have the same mass.

Mass of water displaced = 200 kg.

Volume of water displaced = mass of water/density of water

= 200/1000 = 0.20 m³.

The volume of the block = mass of block/density of block

= 200/570 = 0.351 m³.

Thus the proportion of the wood under the water surface is:

0.20/0.351 = 0.57.

FLUID FLOW: BERNOULLI’S PRINCIPLE

The principles of fluid flow were first explained over two hundred years ago by Daniel Bernoulli, although it is unlikely that he foresaw all the modern applications of his theories.

Imagine a liquid flowing through a tube shaped as in the figure below.

^{Images drawn by me}

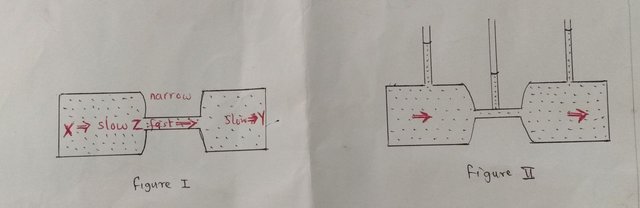
The flow is continuous – just as much liquid enters at X as leaves at Y. For this to be true, the liquid must flow faster in the narrow part of the pipe than it does in the wider parts. For a liquid flowing through a tube of cross-sectional area A at a speed v, the volume passing any point each second is Av. As A varies, so will v – provided the liquid is incompressible. At the pressures normally found in practical situations, liquids are incompressible. Thus, for a liquid flowing in a pipe of varying cross-sectional area, the quantity Av stays constant. This is principle of continuity for a liquid.

Gases are more easily compressed, however, and if the pressure changes as the pipe widen or narrows the gas density will change. What must be constant is the mass of gas that enters and the mass that leaves any section of pipe; it will help to think of this in terms of the number of molecules that enter and leave the section. At any given values of area A and speed v, the mass of gas of density ρ in the section v metres long is pAv. In this case, we express the principle of continuity in its more general form as:

ρAv = constant

Returning to the case of liquid flow, the liquid moves because somewhere back along the pipe there is a pump (say) producing a pressure, which is the same everywhere within the liquid. Now think about what must be happening at Z in the figure above. Here the liquid is being accelerated to increase its speed. Acceleration requires a net force acting in the direction of the acceleration. There must, therefore, be a greater pressure to the left of Z than there is to the right.

The second figure (II) shows a demonstration of the pressure differences in a model of the arrangement. The vertical tubes act as manometers, with the heights of liquid columns measuring pressure. The columns show that the pressure in the narrow tube is less than that in the wide tube in front of it, as theory predicts.

The pressure increases again in the second wide tube – because the liquid is being slowed down and a force is required to decelerate it. This accounts for the differences of pressure shown in the figure II, and Bernoulli’s conclusion was that, in a moving fluid:

The greater the speed, the lower the pressure.

This is Bernoulli’s principle and applies to all fluids, and is the key understanding of why ‘heavier than air’ aeroplanes can stay in the air so long as they keep moving.

^{Condensation visible over the upper surface of an Airbus A340 wing caused by the fall in temperature accompanying the fall in pressure.. Mgw89, CC BY-SA 3.0}

I will be stopping here for now. In my next post, I will discuss the applications of Bernoulli’s principle, streamlines and turbulent flow and the effects of drag on a vehicle. Till then, I still remain my humble self, @emperorhassy.

Thanks for coming by.

REFERENCES

https://en.wikipedia.org/wiki/Pressure

https://www.toppr.com/guides/physics/force-and-pressure/introduction-to-pressure

https://www.asu.edu/courses/kin335/documents/Fluid%20mechanics.pdf

https://simple.wikipedia.org/wiki/Pressure_in_liquids

https://www.brightstorm.com/science/physics/solids-liquids-and-gases/liquid-pressure/

https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/Map%3A_University_Physics_I_-_Mechanics%2C_Sound%2C_Oscillations%2C_and_Waves_(OpenStax)/14%3A_Fluid_Mechanics/14.2%3A_Measuring_Pressure

https://en.wikipedia.org/wiki/Pressure_measurement

https://www.thermalfluidscentral.org/encyclopedia/index.php/Pressure_measurements_and_instrumentation

http://www.gard.no/web/updates/content/20651856/why-do-ships-float

https://www.explainthatstuff.com/how-ships-work.html

https://en.wikipedia.org/wiki/Talk:Archimedes/Archive_1

https://www.teachengineering.org/lessons/view/uoh_fluidmechanics_lesson01

https://www.britannica.com/science/Archimedes-principle

https://opentextbc.ca/physicstestbook2/chapter/archimedes-principle/ 

https://www.youtube.com/watch?v=2RefIvqaYg8

https://study.com/academy/lesson/archimedes-principle-definition-formula-examples.html

https://www.britannica.com/science/Bernoullis-theorem

http://physics.bu.edu/~duffy/py105/Bernoulli.html