The collapse of the Silver Bridge happens to be the worst bridge disaster to have ever happened in the United States. The sad incident which occurred on December 15, 1967, in West Virginia claimed the lives of 46 people. The damage was as a result of a broken eye-bar (I-bar) that was used to construct the bridge. An eye-bar is a type of straight metal bar with a hole at its end where other metal bars can be connected.[source](https://en.m.wikipedia.org/wiki/Eyebar) It is usually used to connect the different parts of a bridge. In the investigation on the collapse of the Silver Bridge, it was later got to know that there had been a little crack in the eye-bar that was used in the construction of the bridge. Due to traffic and a heavy load, the little cracked eye-bar gave way and led to the collapse of the bridge. Isn’t it fascinating for us to know that a defect of just 2.5 mm deep is enough to wreak havoc resulting in the loss of many lives and properties?
A similar case was also witnessed in 1968, in the construction of the Melbourne Bridge in Australia. The architects and engineers committed a simple calculation error which led to a “not-too-simple” repercussion. It was so big a mistake that led the steel girder box of the bridge to become unstable and expand uniformly when heated. This eventually caused the entire length of the bridge to fall off.
 )
)
The Golden gate bridge in San Francisco, US.
An example of a suspension bridge.
Source:[pixabay, CC BY-SA 2.0](https://pixabay.com/photos/golden-gate-bridge-san-francisco-388917/)
Structures are meant to be stable irrespective of the forces that are acting on or against them. Taking skyscrapers, for instance, regardless of the gravitational and wind forces against them, they should be constructed in such a way as to be able to withstand those forces. A suspension bridge should be stable despite the force of gravity pulling it down and the constant movement and thrust it sustains from trucks and cars. One of the major point of this discussion is understanding what allows the stability of such structures irrespective of the forces against them. In that regards, there are two major aspects that ensure the stability of structures: they are basically the equilibrium of forces acting on rigid bodies and the elastic effects on non-rigid bodies. These are the properties that govern how structures can deform. When the physics behind these properties are properly implemented, they tend to be the subject of numerous articles in newspapers and journals, so also is the case if they are not properly done.
So, this is a sequel to my last post on understanding the effects of forces in structures and microstructures in which I explained what structures are, the ideas behind building of structures, how structures do stay up, the center of gravity, coplanar forces and various ways of determining the resultant of two or more forces. In the concluding part of the post, I wrote that there are still many more effects of forces on a structure, some of which are non-coplanar forces, moments of force, like that in a tower crane and many more to come. So, I’ll be shedding more light into some of those effects, starting with Non-coplanar forces i.e forces not acting at a point.
 )
)
A simple diagram drawn by me to explain the principle of moments
F1x1 + F2x2 = f1x1 + f2y2 (Nm)
If an object is in static equilibrium, it remains stationary (at rest) or moving at constant velocity because no resultant force acts on it. A body is in equilibrium when the net forces acting on it are zero and also when the net moment of these forces is zero. A Tower crane is a very good example of the application of moment of forces.
 )
)
A tower crane.
Source:[pixabay, Author: HeungSoon; CC BY-SA 2.0](https://pixabay.com/photos/industry-tower-cranes-sky-equipment-3200185/)
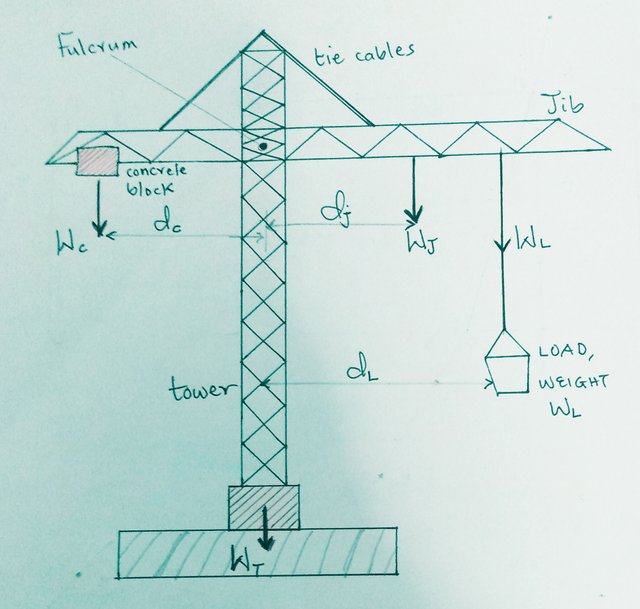
Diagram of a tower crane, displaying the main forces involved. The effect of gravity on the mass of the tower crane will produce a downward force **WT** which acts directly through the tower base. The jib (i.e the horizontal arm of the crane) stretches outwards from the tower on two opposite sides. If observed carefully, it will be seen that the jib extends further outwards on the side used for lifting the load. So, the centre of gravity of the jib lies a distance **dJ** outwards on this side of the tower, and there is a force downwards of **WJ** due to the weight of the jib. Tie cables are provided to help support the jib.
A load **WL** is being lifted at a distance **dL** along the jib from the centre of the tower. A concrete block acting as a counterbalance is positioned at distance **dC** on the opposite side, creating a downward force **WL**.
 )
)
A simple diagram of a tower crane drawn by me, showing the main forces involved.
Using the principle of moments, we choose a fulcrum or pivot point about which to take moments. We take the fulcrum as the point where the jib is fixed to the tower crane. Though, at an engineering point of view, it is crucial to include the tie cables to absorb much of the strain on the jib, but that will be avoided in this instance when calculating the moments. It can be assumed that they are well proportioned, so that the tensions in each are the same. Using the principle of moments, then we arrive at:
#### (WC × dC)concrete = (WJ × dJ)jib + (WL × dL)load
So, for the tower crane to remain balanced and not topple, the turning moment of the block on the left of the equation must counterbalance the sum of the turning moment of the jib and the load on the right.
When you watch a tower crane in action, you will observe that the load is moved into the proper position not only by turning the crane but also by moving the load away from the equilibrium position that’s already been calculated.
We can now see the need for the tie cables. As the load moves away from the equilibrium position, the tie cables take up unequal tensions so that the turning moments remain balanced. The forces in the tie cables must be balanced by forces exerted by the tower crane. The concrete block counterbalance can sometimes be moved after erection, but it can’t be precisely positioned to balance the load. In addition, there will be some extension and bending of the crane parts to “take up” the forces. A full calculation is complicated. In practice, a tower crane is tested for stability with appropriate loads before being put to use.
Let’s look at this sample problem to understand how tower crane operates in real life.
Assume a tower crane is used to lift a load of 50 bags of cement each of 50 kg. The concrete counterbalance, a distance dC of 15 meters from the crane’s fulcrum, is of mass 3000 kg. The jib of the crane creates a downward force WJ of 5 000 Newtons at a distance dJ of 5 meters from the fulcrum. At what distance from the fulcrum must the load be lifted for the tower crane to be in equilibrium?
For us to know the distance from the crane’s fulcrum at which the load must be lifted to attain equilibrium, we employ the principle of moments:
#### (WC × dC)concrete = (WJ × dJ)jib + (WL × dL)load
And from elementary physics, the weight (W) of a body is given as the product of its mass (m) and the acceleration due to gravity (a constant “g” that is approximately 10 m/s2) i.e W =m×g = mg.
The mass of the concrete MC is given in the question as 3 000 kg;
So, the weight of the concrete, WC will be the product of the mass of the concrete MC and the acceleration due to gravity (g) i.e
#### WC = MC × g = 3 000 kg × 10m/s2 = 30 000 Newtons.
The distance between the concrete and the fulcrum, **dC**, is given as 15 metres.
**WJ**, which is the weight of the jib is given as 5 000 Newtons.
The distance between the jib and the fulcrum, **dJ**, is 5 meters.
The weight of the load, **WL**, can be obtained by multiplying each of the 50 bags of cement by 50 kg and then multiply the result with the acceleration due to gravity which is approximately 10m/s2 i.e:
#### WL = 50 bags × 50 kg × 10 m/s2 = 25 000 Newtons.
Let us now substitute all these values into the formula for calculating moments, i.e:
#### (WC × dC) = (WJ × dJ) + (WL × dL)
#### 30 000 × 15 = (5 000 × 5) + (25 000 × dL)
#### 450 000 = 25 000 + 25 000 dL
#### 25 000 dL = 450 000 – 25 000
#### 25 000 dL = 425 000
#### dL = 17 metres.
So, this means that the distance from the fulcrum by which the load must be lifted for the tower crane to be in equilibrium is 17 meters. All these calculations really go a long way in ensuring the stability of structures not only for the tower crane but other structures such as the suspension bridge.
 )
)
Brooklyn bridge
Source:[pixabay, Openclipart; CC BY-SA 2.0](https://pixabay.com/vectors/suspension-bridge-brooklyn-bridge-146870/)
The engineer would also take account of the forces of tension within the steel wires carrying the roadway, and the forces of compression within the reinforced concrete towers and then select those materials that would endure the huge forces exerted on the bridge. Steel is a material known to be strong enough to withstand large tension forces as compared to concrete which is most suitable only for compression forces. An experienced engineer will never suspend a bridge with concrete rods, despite the fact that loading pre-stressed steel into concrete does allow the ensuing composite material to withstand forces of both tension and compression. It is evident then, that to select the best materials for a particular structure, we need to look out more about the individual properties of the materials.
 )
)
An illustration by me showing the stability of a tower.
At that stage, there is now a moment of the gravitational force which is acting about the contact edge of the tower as a pivot point and cause the tower to tilt further and eventually collapse if the situation is not salvaged. It was for this danger of toppling, that the civil engineers had to bring the Leaning Tower of Pisa closer to the vertical position.
 )
)
 )
)
##  )
)Forces not acting at a point
In all the illustrations and examples I gave in my previous [post](https://steemit.com/steemstem/@emperorhassy/understanding-the-ef-1552084478), it can be observed that the forces act just through a single point. But, in a situation of very large structures, it is somehow hard to analyze the forces following this way. We may discover that there are some forces which are acting parallel to one another. So, to fully comprehend how static equilibrium can exist in a condition of forces, not all acting at a point, I need to introduce the concept of moment of forces.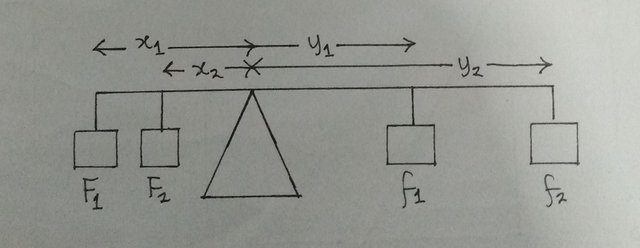 )
)The idea behind “moment of forces”
The principle of moments explains that when a body is in equilibrium, the sum of anticlockwise moments about the pivot (balance point) is equal to the sum of clockwise moments for example, where F and f are in Newtons and x and y are in meters: ####Tower Crane
A tower crane is a very tall machine (up to 150 feet) for lifting heavy tools and objects such as concrete, steel and various types of building materials for the purpose of constructing giant structures. A simple diagram of a tower crane with its caption is drawn below. )
) )
)The Suspension Bridge
An engineer constructing a suspension bridge like that shown in the diagram would take cognizance of all the forces acting at a point inside the structure and the turning moments of the forces. )
)Toppling
If a structure such as a skyscraper or a tower is vertical, the gravitational force on it acts through the center of gravity and also through the center of its ground area. In a condition where the tower tilts, it will still maintain its balance and stay upright so far the walls remain undamaged until the center of gravity stops to lie over the contact area of the tower with the ground. If the tower should go beyond this point, then it will topple.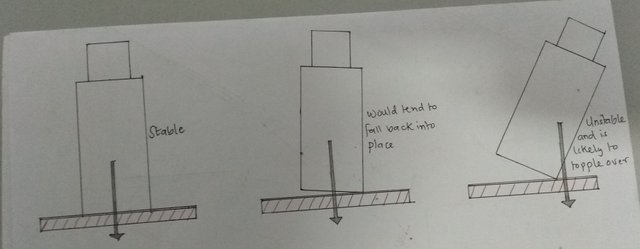 )
)Conclusion
To sum it up, stability is a very crucial effect on structures. Also, neglecting some minute details in construction can lead to great destruction where many lives and properties are lost. Tall buildings such as towers should be constructed in such a way as to be able to endure both gravitational and wind forces. Not only that, structures such as bridges are to be constructed in a way to be able to withstand both the tensional and compression forces. The two main factors that ensure the stability of structures are the equilibrium of forces and elastic effects acting on them. We also got to understand that a tower crane operates on the principle of moments i.e the sum of the total clockwise moment must be equal to the sum total sum of the anticlockwise moments. And, for a tower crane to remain at equilibrium and not overturn, then the turning moment of the block must balance the sum of the turning moment of the jib and the load. Also through the use of moments, a simple calculation such as in calculating the distance from the fulcrum a heavy load must be lifted for a tower crane to be balanced. Also, for an engineer building a suspension bridge, he must factor in all the forces acting within the structure. He must understand the properties of each of the suitable material to use to accommodate the tension and compression forces on the bridge. In the construction a tall structure, special note must be taken of the gravitational and wind forces acting against the structures so as to avoid a case of toppling. Till next time, I remain my humble self, @emperorhassy ## Thanks for reading.  )
)
REFERENCES
[Principle of moments](http://www.passmyexams.co.uk/GCSE/physics/turning-effect-forces.html) [How Engineering bridges handle stress](https://bridgemastersinc.com/engineering-bridges-handle-stress/) [Effects of force on structures](https://www.questia.com/library/journal/1G1-93089425/the-effects-of-force-on-a-structure-strength-and) [Forces That Can Act on Structures - Wrdsb pdf](https://www.google.com/url?sa=t&source=web&rct=j&url=http://teachers.wrdsb.ca/goodacre/files/2014/03/sci7_unit_b_sec04-02.pdf&ved=2ahUKEwiohtCYvPTgAhX1URUIHTwuDFAQFjABegQIDhAE&usg=AOvVaw2R2JGr-y7JWmhsSGLCj7ci) [Structures and forces pdf](https://www.google.com/url?sa=t&source=web&rct=j&url=http://www.edquest.ca/pdf/sia74-2notes.pdf&ved=2ahUKEwiohtCYvPTgAhX1URUIHTwuDFAQFjAUegQIBhAB&usg=AOvVaw1dQmV6zSI6_oTINZBX3vuQ&cshid=1552114499013) [How tower crane works](https://science.howstuffworks.com/transport/engines-equipment/tower-crane.htm) [The collapse of the Silver bridge](http://www.discoveryeducation.com/teachers/free-lesson-plans/stable-and-unstable-structures.cfm) [The eyebar](https://en.m.wikipedia.org/wiki/Eyebar) New School Physics by Dr M.W Ayankoha, Scalars and Vectors, Book 2 Chapt. 1; pg 115 Collins Advanced Science - Physics by Ken Dobson, David Grace and David Lovett Chapt. 5; pg 98  )
)
 )

 )
)
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This is a really good post that deserves strong rewarding .
If you had turned your post into a question and answer, it would have been ideal material for StemQ as well.
Well done.
Posted using Partiko Android
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks for coming by @irelandscape.
Actually, It didn't occur to me to turn the post into a question and answer maybe cos I've actually not written a post in such format before and secondly, I don't really understand much about StemQ and how it works. I'll so much appreciate if you can run me through the process, guidelines and what it's entirely all about.
Thanks, once again.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
StemQ us a Q&A app for stem subjects. People can post questions and wait for others to provide answers.
But it's also possible for the same person to answer his/her own question.
This can be an interesting way to write about a particular topic.
Here is an example:
https://www.stemq.io/question/irelandscape/what-is-the-physical-meaning-of-maxwell-s-equations
Cheers.
Posted using Partiko Android
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks, I'll look into it.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Our Third Mainland Bridge in Lagos Nigeria is consistently overloaded, I just hope it's not a disaster waiting to happen.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks, @greenrun.
Well, I hope so too. The more reason the bridge needs to be properly maintained. I am sure the load the Third Mainland Bridge was carrying or estimated to be able to carry during the time of construction isn't as much as the present load it's carrying. The population of Lagos keeps doubling while special attention isn't given to the bridge.
Just like you've said, I hope we are not all sitting on a ticking time bomb that's about to explode.
I pray!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Although it seems to carry out some periodical checks on the bridge to ensure reliability, I just hope that it is a thorough one.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
If that's the case, then that's fine. I hope it's a thorough and effective check too.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Atimes crossing the river niger bridge in Onitsha gets me trembling. Heavy truck are always moving on it. There was a time it cracked, however, it has being fixed.
In my suggestion, such bridges should have people monitoring the force exerted on the bridge by various vehicles.so that they would stop other vehicles form approaching when the maximum tensile strength of the bridge/structure has being reached by the due to the loads(vehicles)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks, ikchris. You are right. The maximum load the bridge can carry should be maintained and not exceeded.
Thanks for coming by.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @emperorhassy! You have completed the following achievement on the Steem blockchain and have been rewarded with new badge(s) :
You can view your badges on your Steem Board and compare to others on the Steem Ranking
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Although i have never really being a structure person, i must say i have learnt a great deal for your write up especially the concepts behind the leaning tower of pisa. I initially thought the leaning effect of the tower was intentional. Awesome write up!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@sunkanmi02, thanks for coming by.
I'm glad you were able to learn a thing or two from the post.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @emperorhassy!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations! This post has been upvoted from the communal account, @minnowsupport, by emperorhassy from the Minnow Support Project. It's a witness project run by aggroed, ausbitbank, teamsteem, someguy123, neoxian, followbtcnews, and netuoso. The goal is to help Steemit grow by supporting Minnows. Please find us at the Peace, Abundance, and Liberty Network (PALnet) Discord Channel. It's a completely public and open space to all members of the Steemit community who voluntarily choose to be there.
If you would like to delegate to the Minnow Support Project you can do so by clicking on the following links: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP.
Be sure to leave at least 50SP undelegated on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I agree with @irelandscape. You explained it very nicely and in a very comprehensive way. Thanks for sharing this! :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You are welcome, @lemouth. I'm glad you found the post explanatory enough.
Thanks for coming by.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit