Bumblebees and Travelling Salesman Problem

_{Source : Pixabay [ CCO Creative Commons ]}

How would you feel, if some one tells you that tiny little bumblebees with even tinier brains are more intelligent than us and computers? Unbelievable, right?

Bumblebees are smart little brains. On a foraging trip, bumblebees collect pollen and nectar from flowers. These smart fliers do not collect their food pointlessly, buzzing around at random flowers. Instead, they work very smartly and efficiently.

According to an experiment held by researchers, some bees and artificial flowers with attached tiny webcams were left in a pentagon to record the bees' movements.
Researchers noticed that each bee chose flowers that were at shorter distance, first.
If one flower had more nectar and pollen than other and travelling distance to that flower was not much longer than others then it chose that flower over others first.
Bees took some time to learn the given environment and designed a shortest optimal route in their mind which they kept following then.

This way of choosing shortest paths is called Travelling Salesman route in Computer Science language and travelling salesman is considered a complex problem till now.

What is Travelling Salesman problem?

_{Source : Wikimedia Commons}

It is a classic computer science problem which has made many scientists rack their brains for years to get the optimal solution. It goes like this:

There is a travelling salesman who has to visit several cities. Starting from one city, he has to return to the city of origin, without traversing any city more than once. Keeping in mind the travel cost, which will be less for shorter routes, he has to choose the best and optimal route.

This sounds easy, right? We just have to calculate all the possible routes and choose the shortest one.

Solution

The data structure used in computer science to solve this problem is Graphs.

Let's assume there is a graph G(V,E) where V is a set of nodes or cities. E is a set of weighted edges. Edge represents any two vertices u and v, connected with each other. The distance between two vertices u and v is d(u,v).

Following equation is used to determine the shortest path.

C ( S , j ) = min C ( S − { j } , i ) + d ( i , j ) where i ∈ S and i ≠ j

This equation suggests to divide travelling salesman problem into sub-problems. Like if a salesman travel from city 1 to the city j, then he should know what was the cost of travelling up to that city and the distance it took to travel. According to this information, he can choose the next optimal destination keeping the total cost and distance as low as possible.

In the above equation, C is Cost, S is sub-set of cities i.e, S= {1,2,3,4,5,...n}, where j also belongs to S.

_{Table form of the graph}

When S = { } , then

(Empty Set means there is no subset of cities between origin and destination)

Cost ( 2, { } , 1 ) = d(2,1) = 7

Cost ( 3, { } , 1 ) = d(3,1) = 8

When S = 1 , then

Cost ( 2 , { 3 } , 1 ) = d(2,3) + d (3,1) = 5+8 = 13

Cost ( 3, {2}, 1 ) = d(3,2) + d(2,1) = 4+7 = 11

When S = 2 , then

Cost (1 , {2,3} , 1} = d(1,2) + Cost ( 2, {3} , 1) = 10 + 13 = 23

Cost (1, {3,2} ,1 ) = d(1,3) + Cost(3, {2} , 1) = 11 + 11 = 22

Now you can see when S = 2, we get minimum value with d(1,3). So we must move from 1 to 3.

When S = 1, d(3,2) has minimum value, so we move from node 3 to 2.

When S = { }, d(2,1) has minimum value so we move from 2 to 1.

_{Shortest path}

Total distance or cost in this case is 22.

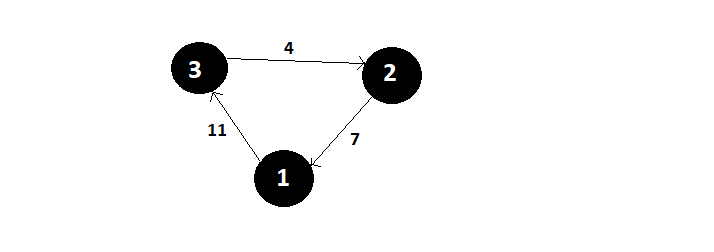
In the above example, I chose three cities to travel. There were just two possible routes and we chose the shortest. But if we look at the general equation for finding all possible combination of routes:

For a graph with n vertices, ( n - 1) ! are possible combinations.

Just think, if a graph has 10 nodes, then there will be 3628800 possible routes which need to be calculated first and then the shortest route would be selected.

You can see how the possibilities increase exponentially when number of cities are still not that much.

Here comes the problem, how a computer would calculate the shortest path, when the possibilities are this much with higher number of cities. Finding each possible route is quite tiresome and would take so much time, power and storage of a computer. This makes travelling salesman problem NP-hard.

( Reading Recommendation : The P vs NP problem by @anevolvedmonkey )

Christofide's Algorithm

Professor of Imperial College of London, Nicos Christofide designed an algorithm and claimed that it gives the route which is just 50% longer than the shortest route.
In 2011, Stanford-McGil team improved the algorithm slightly i.e, 49.999...6 % longer than the shortest route.

_{Graph with higher number of nodes}

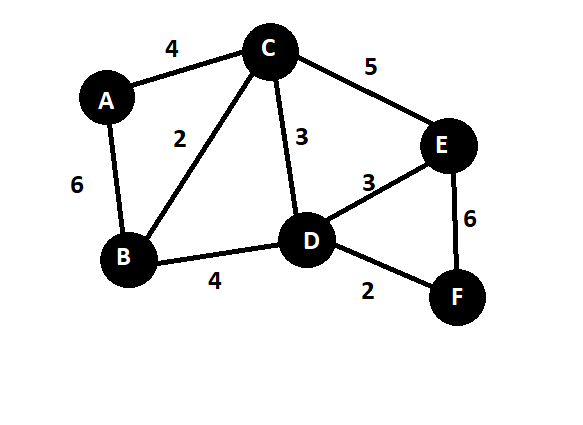
Following are the steps of algorithm for a given graph whose edges obey triangle inequality.

_{Minimum Spanning Tree}

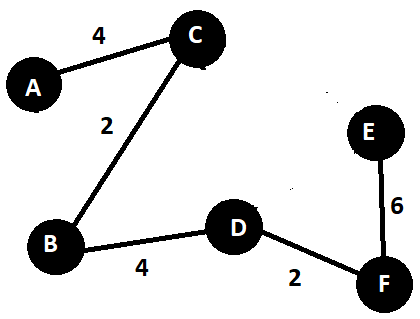
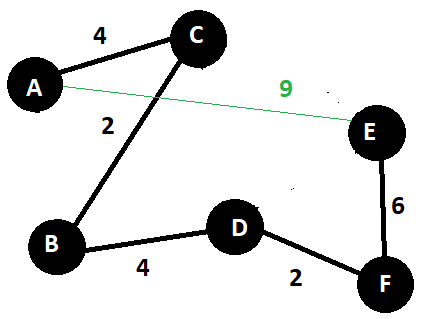
Calculate Minimum Spanning Tree of the given graph.
( Set of edges with minimum total weight that connect all vertices ) In the diagram you can see A -> C -> B -> D -> F -> E is the shortest combination for spanning tree.

_{Even Degree Graph}

Find the vertices with odd degrees and convert them into even degrees.
( Degree of a vertex is the number of edges, a vertex is connected to )
A and E are connected to one vertex, their degree is 1. B, C, D, F are connected to two vertices, their degree is 2. So A and E are connected making their degree even.

_{Minimum-Weight Perfect Matching}

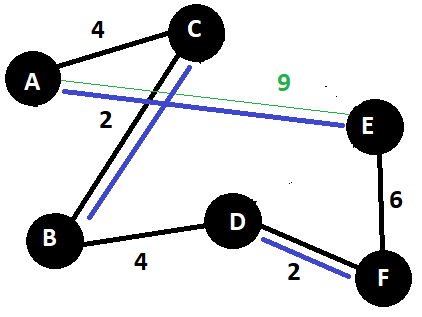
Now construct minimum-weight perfect matching of the above even degree graph.
Matching graph has set of edges which have uncommon vertices.
Perfect matching graph involves all the vertices of a graph.
Minimum-weight refers to the total weight of perfect matching to be minimum. AE, BC and DF edges have the minimum total weight here.

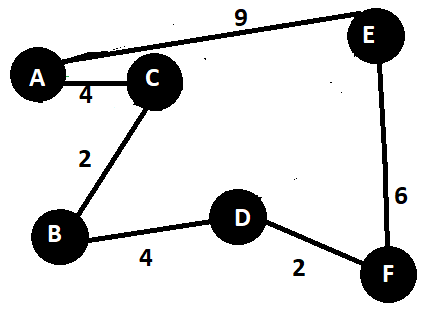
_{Union of Spanning Tree and Minimum-Weighted Perfect Matching}

Now unite minimum spanning tree graph and minimum-weight perfect matching. In other words take the union. ( I have slightly moved the nodes for clarity ). Observe the changes from the original graph.

_{Euler's Tour}

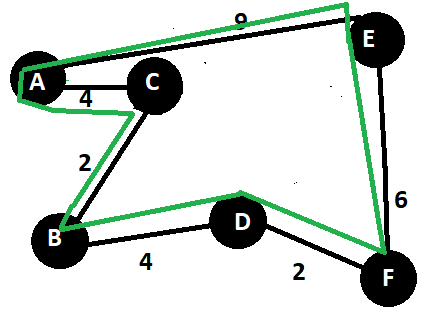
Find Euler tour of this newly constructed graph.
(Euler path touches each edge of the graph only once and covers all vertices). In the diagram, green line shows the euler path.

Next step is to find Hamiltonian path(Removal of repeated vertices) which is not needed in this case as there are no repeated tours to a vertex.

This gives us the optimal route with cost 27.

Till now, this is the best method of solving travelling salesman problem. It's not accurate and since it was designed, people are trying to improve it. Many have succeeded in getting a bit closer to accurate result.

One technique was to use fractional way to achieve better results. Like travel from place A to C and from place B to C and then round off both the fractional trips to get an approximate one. It's impractical but many mathematical problems are solved this way. This method claims to give 40% longer route than the shortest.

Now I am truly amazed at bumblebees, do they calculate this much math while on foraging trips. Or is it us only, who need complex algorithms to solve the case. I hope some day we get an insight into bees' minds to know their secret algorithm.

Like mentioned before, Travelling Salesman Problem is NP-hard for a reason. If this problem is solved, world of technology would turn upside down.

Talking about this, it reminds me of a personal problem. I lost a password of a zip file in my computer. I tried every software to crack it but all in vain. To make it worse, I couldn't even recall a single character in my password. So there were millions of combinations my computer had to check using brute-force. I even tried to run a software for 3 days. All it did was make my computer slow.

Back then I didn't know it's impossible because that was NP-hard. If I could have resolved that issue then that means there would also be no privacy in the world of tech. Because encryption techniques would fail.

References

Note: Non-credited images are my work.