This small tutorial to explain one of the cases of the division of fractions, does not pretend in any way to replace the information that in this respect appears in any book of mathematics, rather it is presented as an alternative to link the knowledge with the reality of the student, and their experiences, in such a way that it can serve as support in the didactic exercise of the teaching referred to this particular content. Hence, the mathematical formalization inherent in it is not presented.
It is based on my experience as an area teacher, at the secondary level and on David Ausubel's theory of meaningful learning, which emphasizes the connection of previous knowledge with new information, within the framework of constructivist psychology.
In our first installment, it was approached by means of some examples contextualized with the student's environment, the way of dividing ½ by 2, which applies to divide a proper fraction among an integer. On this occasion we try to illustrate the way of dividing 2 between a medium, that is, the opposite process.
How much is 2 divided by ½?
The answer to this question leads in turn to ask:
How many times does it fit in two units?
How many times does 2 contain ½?
How many halves can fit in 2 units?
And this situation can be contextualized as follows:
How many times does half a cup of chocolate fit into a container that contains 2 cups?
How many half cups of chocolate are required to fill a container that contains 2 cups?
With two half cups filled halfway, the container given; that is, complete a cup. With two additional cups complete the entire container. That is, I need four half cups to fill the container.
In this context, two divided by a half, represents four halves. Four half parts
Each unit has two halves, therefore two units represent 4 halves.
Another example related to our daily work, could be:
How many half liters of milk do I need to complete 2 liters?
Graphically:
In the attached figure, 2 rectangles are observed in the upper part and in the lower part each of the previous rectangles is shown divided in two equal parts. Note that each rectangle above corresponds to two rectangles below.
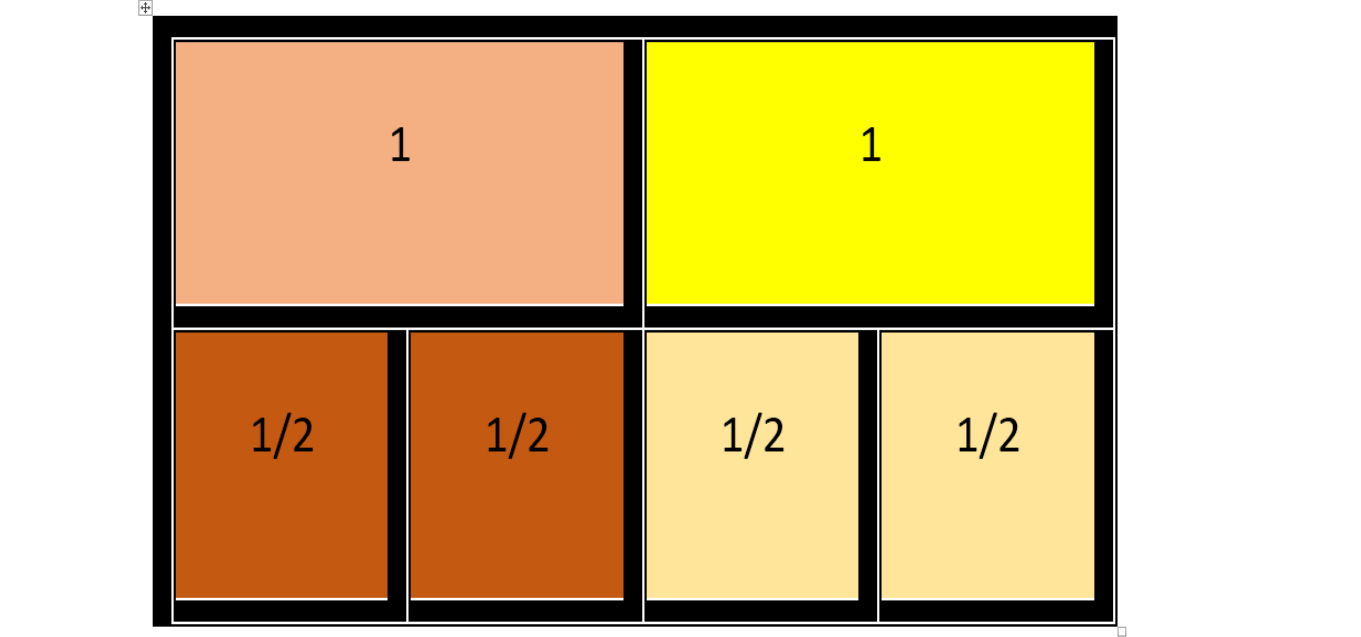
How many halves fit in each rectangle?
Observing the graph, it can be seen that in each rectangle fit 2 halves.
How many halves fit in the two rectangles?
When you draw a rectangle after the other, you can see that in the two rectangles fit 4 halves.
Then, 2 divided by a means equals 4.
BIBLIOGRAPHIC REFERENCES
The meaningful learning theory of David Ausubel
Content planning for 1st year of Basic Education. Higinio Villalobos. Maracaibo Venezuela.