Basic principles of dynamics.
It is never bad to remember the basic things that are the basis of the largest studies of any area, so in this article, I bring you a recapitulation of the basic principles of dynamics.

Source
It is known that statics deals with the study of forces; the kinematics, the movement in terms of trajectories, spaces and times, without addressing the causes, that is, the forces that produce it. The dynamics are classified as:
- Dynamics of solids.
- Fluid dynamics or hydrodynamics.
- Gas or aerodynamic dynamics.
In turn, the dynamics of solids is subdivided into:
- Dynamics of the point, which refers to those bodies that only have translatory movements, in which case they can be studied as if all their mass were concentrated in the center of gravity.
- Dynamics of the rigid solid, which refers to the bodies that have rotation movement, independently of whether they possess movement of translation or not.
Principles of dynamics.
The studies carried out by Newton led him to establish the following laws or fundamental principles of the dynamics:
The principle of inertia.
"Everybody is kept at rest or in uniform rectilinear motion in which it is found until a force acts to change it."
The experimental verification of this principle is extremely difficult because if it is tried to verify it and a sphere is thrown for example by a horizontal plane, it is verified that at a certain moment it stops. The cause is that on it act forces that cause this situation: the friction with the plane and the air. If those forces were canceled, the sphere would continue its trajectory with equal speed and without stopping; that is, in the ideal conditions the enunciated principle is fulfilled.
The principle of mass.
"If a force acts on a body, it receives an acceleration proportional to the direction of the force and of the same direction."
If a force acts on a body, it can not be at rest nor can its movement be uniform rectilinear, but it will be characterized by an acceleration.
If the force is of constant intensity, direction, and direction, the acceleration will also be so and the principle is satisfied that the ratio between the acting force and the acceleration that it produces are constant. That constant is the mass (m).
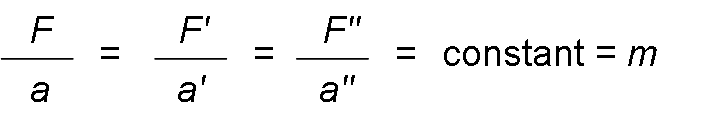
If the force is the weight and the acceleration is the gravity:
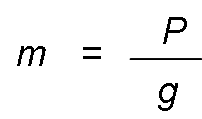
From this it can be assured that:
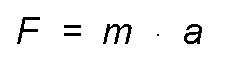
The principle of action and reaction.
"Whenever a body exerts a force (action) on another, the second will exert, on the first, a force of equal intensity and direction but of the opposite direction (reaction)."
It is already known in statics that every reaction is opposed by a reaction (opposing force). This is also true for actions between bodies. A body resting on a plane produces the force-weight action on it and, in turn, the plane produces a reaction that is the same and opposite.
The principle of independence of action of forces.
"When several forces act on a body, each one produces an acceleration that does not depend on the other forces."
Accordingly, to estimate the acceleration produced in a body by a system of forces, one can directly calculate the acceleration produced by the resultant or the sum of the accelerations produced by each of the intervening forces.
Units of force.
International system.
The unit of force in the international system is called Newton.
Newton is the force that applied to a mass of one kilogram, communicates an acceleration of one meter per second squared. It is represented by N.
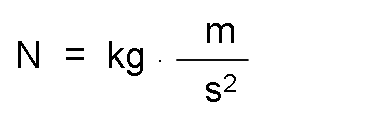
Cegesimal system.
The unit of force in the cegesimal system is called Dyna.
Dina is the force that applied to a mass of one gram, communicates an acceleration of one centimeter per second squared. It is represented by dyn.
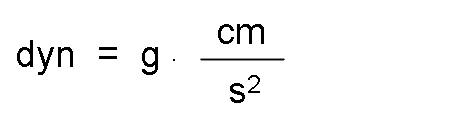
Technical system.
Force is one of the fundamental magnitudes of the technical system; it is for this reason that its corresponding unit - the kilopond - is not obtained from others, but is established as a standard unit.
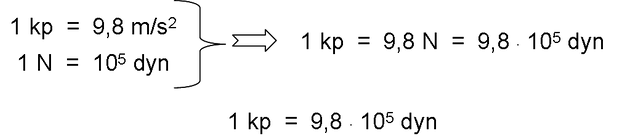
Kilopond is the force with which the Earth attracts in Paris to the mass kilogram. It is represented by KP.
Equivalence between the units.
The equivalence between the Newton and the dyna can be easily obtained, just by considering the relationship between the mass and acceleration units in the respective systems.
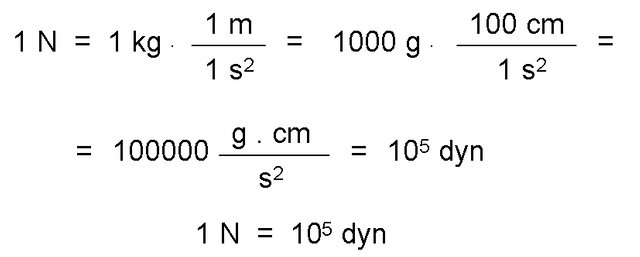
To obtain the equivalence between kilopond and newton, we must consider that:
- The Earth exerts an attraction force of 1 kg on the mass kilogram, and prints, as for all bodies, an acceleration of 9.8 m / s2.
- On the other hand, as previously studied, when a force of 1 N acts on a mass kilogram, it prints an acceleration of 1 m / s2.
Taking into account the existing proportionality between force and acceleration, we can express:

From the consideration of the two previous relationships, it results:
Dimensional formula.
Force is a fundamental quantity in the technical system, whereas it is not in the international and cegesimal systems.
- In the international and cegesimal systems, since force is the product of a mass by an acceleration, its dimensional formula is obtained by multiplying the dimensional formulas of mass and acceleration.
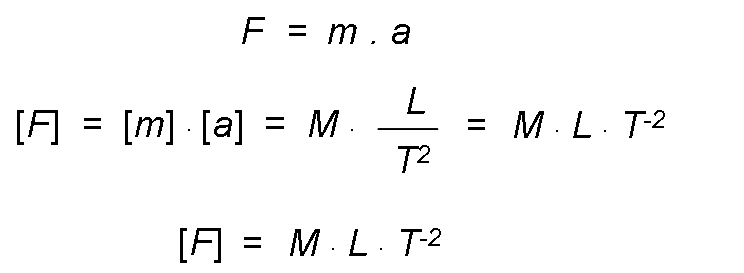
- In the technical system, since force is a fundamental quantity, its dimensional formula is:
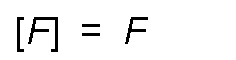
Mass calculation.
As seen previously:
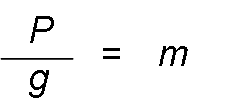
And:
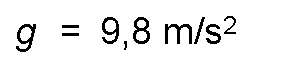
That is to say that, knowing the weight of a body in a place and the value of gravity in that place, the mass of said body can be calculated.
Units of mass.
International and cegesimal system.
As it is already known, the units of mass in the international and cegesimal systems are the kilogram and the gram, respectively, which are represented by kg and g.
Technical system.
The mass unit in the technical system is called the mass technical unit.
Technical unit of mass is the mass that a body must possess so that, when applying a force of one kilopond, acquire an acceleration of one meter per second squared. It is represented by utm.
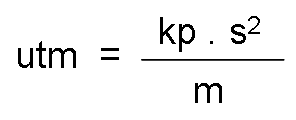
Equivalence between the units.
To calculate the equivalence between the technical unit of mass and the units of the other two systems, it is enough to relate the corresponding units of force, length and time. A) Yes:
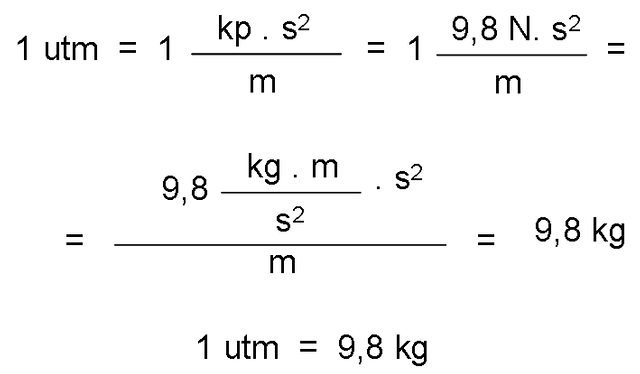
On the other hand, considering that 1 kg = 1000 g, we obtain:
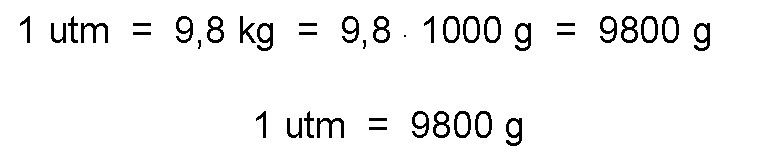
Dimensional formula.
The mass is a fundamental quantity in the international and cegesimal systems, while it is not in the technical system.
- In the international and cegesimal systems, because it is a fundamental quantity, the dimensional formula of the mass is:
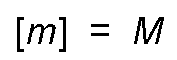
- In the technical system, when the mass is the quotient that results when dividing the force between the acceleration (principle of action of the forces, its dimensional formula is obtained by dividing the dimensional formulas of force and acceleration:
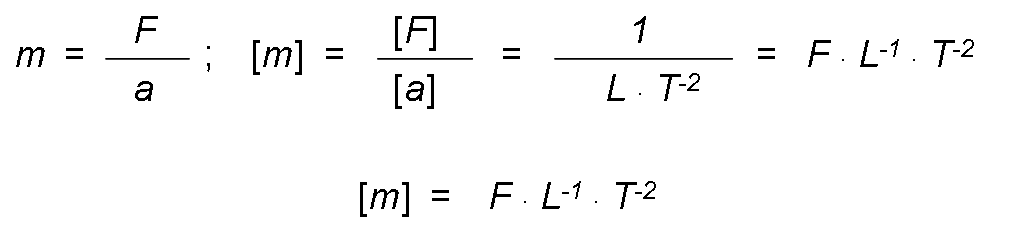
Impulse and amount of movement.
When a force F acts on a mass m transmits an acceleration.
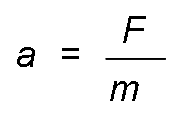
From where:
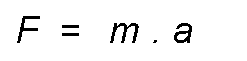
More if that force acts for a time t, it is called impulse to the product of force for the time during which it acts.
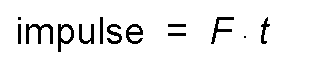
Replacing:
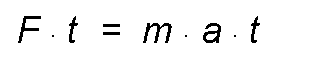
Being:
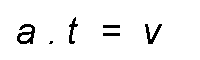
Result:
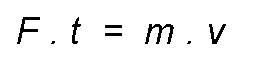
The product m. v is the amount of movement, therefore the impulse is equal to the amount of movement.
The definition of momentum referred to a body can be extended to a system formed by two or more bodies endowed with different speeds; thus the amount of movement of a system formed by two masses m1 and m2, which move with the velocities v1 and v2, will be:
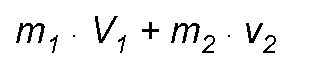
It should be noted that, given the vectorial character of the velocity, the two masses of the previous system may have entirely different directions and directions of movement. If these systems are not subject to any external force, or, as they say, physically constitute an isolated system, a very important general principle called the principle of the conservation of momentum can be applied to them, the statement of which is as follows: an isolated system the total amount of movement is constant.

Applying the previous case we would have:
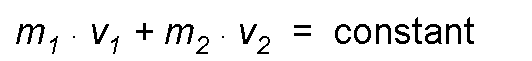
A clear application of this principle is in the weapon + projectile system; before the shot its movement amount is 0, since the system is at rest; when making the shot, the shell of mass m1, which travels at a speed v1, has an amount of movement m1 . v1 To cancel this effect, it is necessary that the weapon acquires an amount of movement equivalent m2. v2, in the opposite direction, so that its total amount of movement is maintained, for which it is necessary that the speed is in the opposite direction.
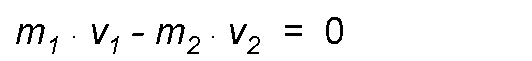
In practice, this phenomenon is clearly seen due to the recoil suffered by the weapon at the moment of firing. This principle also has application in the problems of shock and is the foundation of the reaction engines.
References:
- https://www.lucidarme.me/fundamental-principle-of-dynamics/
- http://ocw.metu.edu.tr/pluginfile.php/6467/mod_resource/content/6/ch6/intro.htm
- http://www.physicsclassroom.com/class/momentum/Lesson-1/Momentum-and-Impulse-Connection
- https://www.compadre.org/precollege/static/unit.cfm?sb=3&course=2
