Suppose we have a two-state cellular automaton using the Moore neighborhood, which counts both orthogonal and diagonal neighbors. How many possible rules are there?
With 9 cells total (including the center one) there are 2^9 = 512 different states or "patterns" of the neighborhood, and each pattern may have either 0 or 1 as the next state for the center cell. That gives 2^512 different rules, about 10^154.
However, it is more usual for 2-D cellular automata to be symmetric with respect to rotations and flips. This group of symmetries is the Dihedral Group of order 4, D_4, which has 8 elements. So a particular pattern may have up to 7 other patterns that should have the same outcome.
Burnside’s Lemma
We can count the number of distinct patterns under this symmetry using Burnside’s Lemma. We just need to identify, for each symmetry (group) operation, how many patterns are fixed under the operation. For example, if we flip along the vertical axis
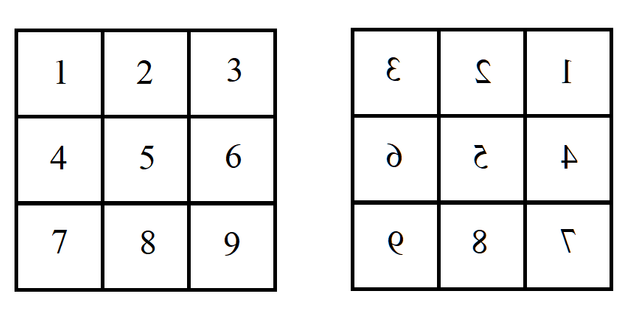
then the pattern is the same only if the corresponding cells match: 1=3, 2=2, 4=6, 5=5, 7=9, 8=8:

We can see that gives us six choices to fill in; the other three cells are determined by the symmetry. The center column cells can be anything; the left and right columns must match.

There are thus 2^6 possibilities that are fixed by flipping along a vertical axis.
For rotation by 90 degrees or by 270 degrees we have three choices, or 2^3 possibilities:
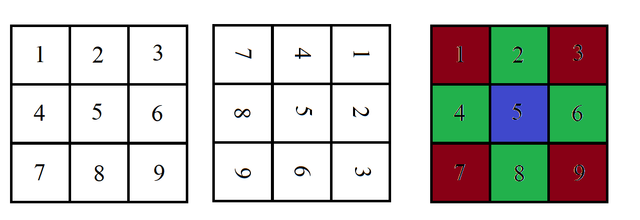
For rotation by 180 degrees we have five choices:
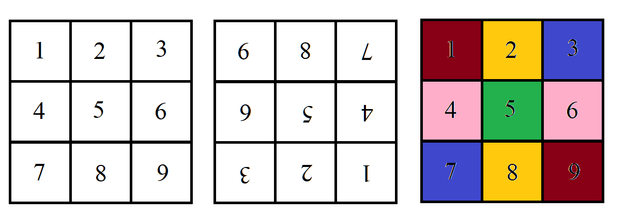
For a flip along the diagonal we have six choices, or 2^6 patterns that are fixed by that group operation.
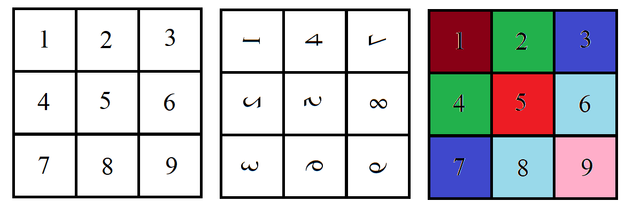
Let's put it all together. The dihedral group can be generated by rotation a and a diagonal flip x:
| Group element | explanation | number of patterns fixed |
|---|---|---|
| e | identity | 2^9 (all of them) |
| a | rotation by 90 | 2^3 |
| a^2 | rotation by 180 | 2^5 |
| a^3 | rotation by 270 | 2^3 |
| x | reflection along diagonal | 2^6 |
| ax | vertical flip | 2^6 |
| a^2x | reflection along other diagonal | 2^6 |
| a^3x | horizontal flip | 2^6 |
Burnside’s Lemma tells us there must be
(1/8) * ( 2^9 + 2^3 + 2^5 + 2^3 + 2^6 + 2^6 + 2^6 + 2^6 ) = 102
distinct patterns, and thus 2^102 possible Cellular Automata (of this type) that respect symmetry. Again, each possible pattern can have two possible outcomes: center cell live, or center cell dead.
Brute Force
Of course, this number is small enough to just enumerate all the possibilities. Using Python, we can represent each pattern by a 9-tuple, and implement the two generators of the group:
# abc gda
# def => heb
# ghi ifc
def rotate( pattern ):
( a, b, c, d, e, f, g, h, i ) = pattern
return ( g, d, a, h, e, b, i, f, c )
def rotate2( pattern ):
return rotate( rotate( pattern ) )
def rotate3( pattern ):
return rotate( rotate( rotate( pattern ) ) )
# abc adg
# def => beh
# ghi cfi
def diagFlip( pattern ):
( a, b, c, d, e, f, g, h, i ) = pattern
return ( a, d, g, b, e, h, c, f, i)
Then for any given pattern, we can create a list of its images under all the possible symmetries:
def symmetries( pattern ):
return ( pattern,
rotate( pattern ),
rotate2( pattern ),
rotate3( pattern ),
diagFlip( pattern ),
rotate( diagFlip( pattern ) ),
rotate2( diagFlip( pattern ) ),
rotate3( diagFlip( pattern ) ) )
Then we blast through all 2^9 possible patterns and only record those we haven't previously seen:
import itertools
patterns = set()
for x in itertools.product( [0,1], repeat=9 ):
tx = tuple( x )
found = False
for s in symmetries( tx ):
if s in patterns:
found = True
break
if not found:
patterns.add( tx )
print len( patterns ), "Patterns found"
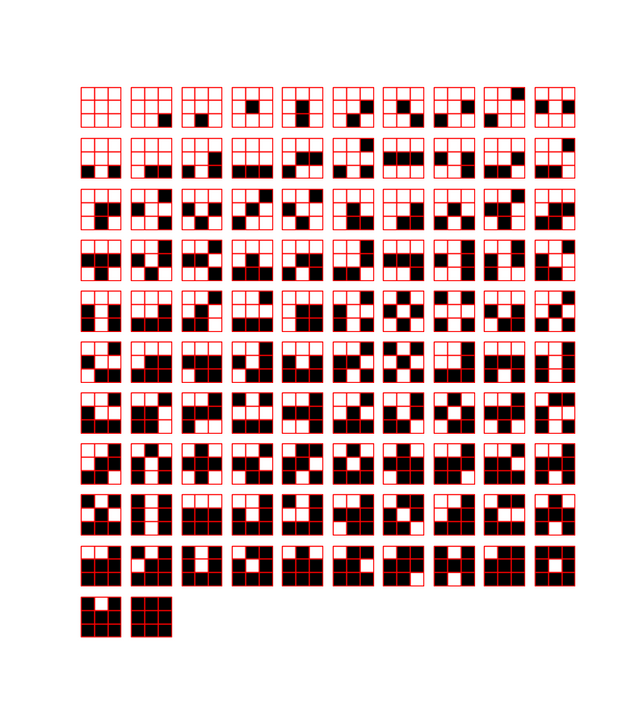
This results in 102, just like mathematics told us it would.
Displaying the results
While we've got a computer enumeration of all the possibilities, we might as well make a nice plot using matplotlib. The same techniques I used here come in useful to make all the plots come out as squares:
from matplotlib import pyplot as plt
from matplotlib.patches import Rectangle
from matplotlib.collections import PatchCollection
scale = 0.32
offset = 0.02
def rectangle( xy, live ):
if live:
return Rectangle( xy, scale, scale, fill=True,
edgecolor="red",
facecolor="black" )
else:
return Rectangle( xy, scale, scale, fill=True,
edgecolor="red",
facecolor="white" )
def drawPattern( ax, pattern ):
( a, b, c, d, e, f, g, h, i ) = pattern
rectangles = [ rectangle( (offset, offset + 2 * scale), a ),
rectangle( (offset + scale, offset + 2 * scale ), b ),
rectangle( (offset + 2 * scale, offset + 2 * scale ), c ),
rectangle( (offset, offset + scale), d ),
rectangle( (offset + scale, offset + scale ), e ),
rectangle( (offset + 2 * scale, offset + scale ), f ),
rectangle( (offset, offset), g ),
rectangle( (offset + scale, offset ), h ),
rectangle( (offset + 2 * scale, offset ), i ) ]
for r in rectangles:
ax.add_patch( r )
#ax.add_collection( PatchCollection( rectangles ) )
def byWeight( pattern ):
return sum( pattern )
def showAll():
for i, p in enumerate( sorted( patterns, key = byWeight ) ):
# 102 patterns fit in 11x10
ax = plt.subplot( 11, 10, i + 1 )
ax.axis( "off" )
ax.set_aspect('equal', 'box' )
drawPattern( ax, p )
plt.show()
showAll()
Output:
Challenge
How many distinct patterns exist in a 3-dimensional 2-state cellular automaton, under rotational and mirror symmetries? There are 2^27 possibilities if we have a "cube" neighborhood instead of a "square", and there are 48 symmetries to work with.
I wanted to make a serious math comment but then
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the SteemSTEM curation team and voting trail in collaboration with @utopian-io and @curie.
If you appreciate the work we are doing then consider voting all three projects for witness by selecting stem.witness, utopian-io and curie!
For additional information please join us on the SteemSTEM discord and to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hi @markgritter!
Your post was upvoted by Utopian.io in cooperation with @steemstem - supporting knowledge, innovation and technological advancement on the Steem Blockchain.
Contribute to Open Source with utopian.io
Learn how to contribute on our website and join the new open source economy.
Want to chat? Join the Utopian Community on Discord https://discord.gg/h52nFrV
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit