How we can create a Black Hole in a simple way?

A Black Hole is a region of space-time where anything can't escape, even not the light. Once an object pass the so called "event horizon" is condemned to fall into the center of the Black Hole. An object can't escape because in order to do so, would need to go faster than light, and as we know that is impossible.
We can create a black hole by ourselves in different ways, in the simplest way, we need a dying supernova. Because dying supernovae are not at sell in the supermarket we have to conform to create not a black hole but something that under certain circumstances behaves similar: An analogous black-hole... So you can forget to destroy your school or job by now.
An analogous black-hole is a system that can behave like a black hole or a white hole (we will come back to this latter), and can be made with waves in water, air or in a superfluid... but the simpler model is with water so we are going to follow with that.
But how we can create a black hole with water? If we take water and create a region where the water flows faster than the speed of sound, the sound that treaspases that region can't return from that region. In that sense, from the point of view of the sound, there is a black hole in the water!
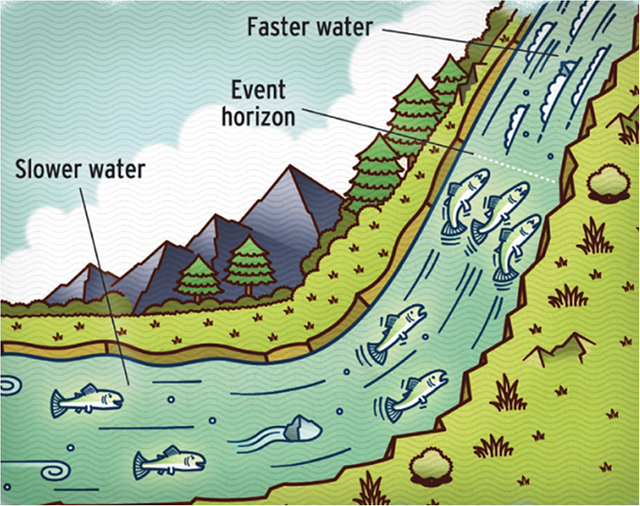
Let's digest that. Imagine that you are a fish who talks and you are near to a waterfall.
If you talks with your fish friends, far from the waterfall, you don't notice anything weird. But near to the waterfall, the water speeds up and begin to carry away your voice. Someone nearer to the waterfall will hear you with a low pitch voice while someone further will hear you with a high pitch. This is also called Doppler Effect.
But, if we go to faster and faster regions in the waterfall, there is a point where the water take away your voice completely and your fish friends in the slow zones can't hear your screams! That happens because the water moves faster than the speed of sound.
The point where the speed of sound and the speed of water equals is called Hydrodynamic Horizon, and behaves in the same way than a Event Horizon in a real black hole. Because the sound can't escape once passed the Hydrodynamic Horizon we have a black hole analogue from the point of view of the sound.
Sooo.. we need a waterfall right? Not so fast. The waterfall was only an example. If you made an analogue Black hole with a waterfall in that way, the waterfall in real life should had to measure hundreds of meters tall. An that is because the speed of sound in water is in reality very fast, and move the water at that velocity is hard. But the waves in the surface moves much slower than the speed of sound, so we can work with that instead.

Wait a minute! In this point, if you know some of relativity maybe you are thinking that something isn't right. The fact that something can't go out of a region does not defines a black hole. A black hole is defined by some complex metric and equations in relativity. And yes, you are right. But in fact the sound in this system can behave with an effective metric that is the same as the Schwarzschild metric.If you don't know, Schwarzschild metric are the metrics that describes an spherical non rotating black hole. The detailed equations are in the APPENDIX 1.
If these terms confuse you, or you doesn't want to read math today, you can skip it and think that under certain conditions the two systems behaves in similar ways.
As you may guess, in order that all this works, we need some previous conditions for the water to behave like a black hole:
- The water can't have turbulence.
- The water needs to be over a rigid floor.
- The water needs to flow in one direction.
- The waves needs to be much larger than the height over the floor (shallow water regime).
- The waves needs to be larger than 2.5 cm for avoiding surface tension effects.
- The water needs to have a section where the velocity surpass the surface waves speed.
Where we can find these conditions? In an open channel.
But the channel has to ensure to have a minimum turbulence and a region of high velocity. For ensure that we need something more controlled. In the photo: the open channel from my university which ensures these conditions.

The channel has an obstacle, this obstacle speeds up the water when the water pass over it. The obstacle, and the quantity of water that are pumped in the channel, are such that over the obstacle the velocity of water overcomes the velocity of the surface waves and creates an Hydrodynamic Horizon!
A detail of the obstacle used in the channel above is in this picture:

What? How a simple obstacle can speeds up the velocity of water? That is due to the flow rate conservation. Under the majority of the conditions, water can't be compressed. So when water moves can't change his volume.
This means that if we measure in an area A1 the volume of water that crosses in each second, it has to be the same that the volume that crosses another area A2 each second. But the volume can be written as the area times the distance that advances the water in a time t. This distance can be written as the velocity of water times t. So in the final we have:
In terms of the velocity V2 in the second area:
If the first area is bigger than the second area, the velocity V2 will raise. In the contrary will go down. We see this effect in a garden hose when we partially blocked the exit of water. And because that, the velocity over the obstacle in the channel raises.

Aaand... we have our analogue of a Black hole! As expected, when we send a wave before the obstacle down to the current, the wave doesn't come back...
Ok... we have a black hole analogue, what we can do with it?
Because the system behaves in a similar ways to a black hole, we can expect to appear effects like Hawking Radiation.

Hawking radiation (yes, from the famous man in the wheel chair) is an effect of black holes where they emits a faint radiation while loses his mass. Explain correctly the effect is hard. Any 2 minutes explanation of this effect will probably be wrong, so don't be confident of the following explanation of the effect:
In all the spacetime are fields that vibrates and creates virtual pairs of particles/antiparticles all the time. These field vibrations aniquilates each others normally and we don't see anything. But in the surroundings of an event horizon, due to the distortion of spacetime, from outside the black hole, some of these "virtual vibrations" are seen as a real particles coming from the black hole. These particles are the Hawking radiation.
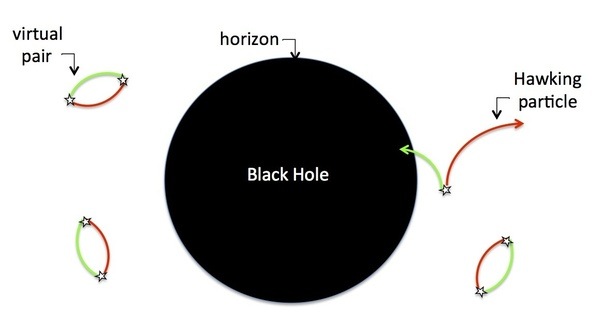
For a better explanation you can search for PBS Space time videos in youtube.
Because the Hawking radiation of a big black hole is in theory too faint, right now is impossible measure it directly. That is the point where our analogue of water takes importance, because in no other way we can study the Hawking radiation in a direct manner. But we can measure it?
Sadly no. In theory the radiation in our water system is too faint that are in the microscopic level, so we can't measure it neither. But we can do other thing. If we excite the vibration modes that generates the Hawking radiation maybe we can generate it. This is called Stimulated Hawking Radiation.
But these vibrations are not arbitrary, they have to be in a certain way in order to generate the Hawking radiation. Generate those vibrations in the channel in a non disrupted way are not easy. So we avoid that doing another thing.
Instead of creating an analogue of a Black Hole, we create an analogue of a White Hole. A White hole is a Black Hole in backwards, instead of absorbing everything, a White Hole expulses everything. Instead of having an Event Horizon where nothing can escape, has an Event Horizon where nothing can't penetrate.
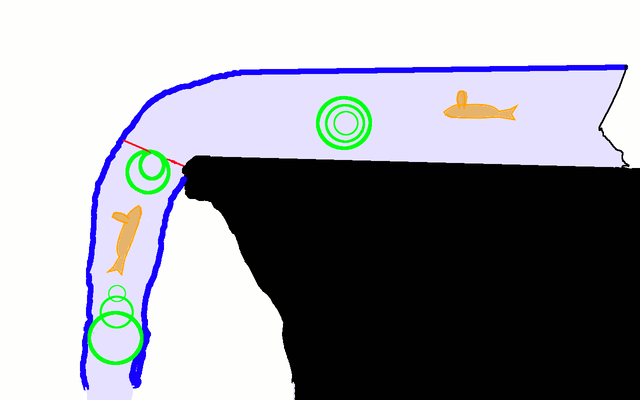
For digest that better, we can look this drawing of the other side of the waterfall:
If the fish talks far from the waterfall, they will not going to notice anything. As they are closer to the event horizon, their sounds begins to being dragged by the water and in the horizon the sounds cannot penetrate. This system is like a white hole where nothing can't enter, and is the same as the analogue black hole but with the time in the other direction.
In this new system, instead of generating the vibrations that produces Hawking radiation, what we do is pump Hawking radiation into the system and see if the vibrations are generated. If the vibrations are generated (and if behaves in the way that are predicted) we can say that we have Hawking radiation! This point of view is more easy to execute because only requires to send a wave into the hydrodynamic horizon.
So... in the channel of my university, the thing sees like this:
In the video, a wave of "Hawking radiation" is sent against the current to the horizon. As get closer to the horizon it gets slower until stops in the horizon. Therefore, we spect the occurrence of two modes of vibrations corresponding to the oscillations that generates Hawking radiation in a Black Hole, BUT... these oscillations are too small to be seen in the video and are mixed with the incident wave.
To ensure that these modes exist and behave in the predicted way, in the lab I had to do precise measurements of the water surface with lasers and cameras. Later I had to do Fourier analysis to unmix the waves and later prove that effectibly the modes are generated as predicted.
This is the water surface illuminated by laser:

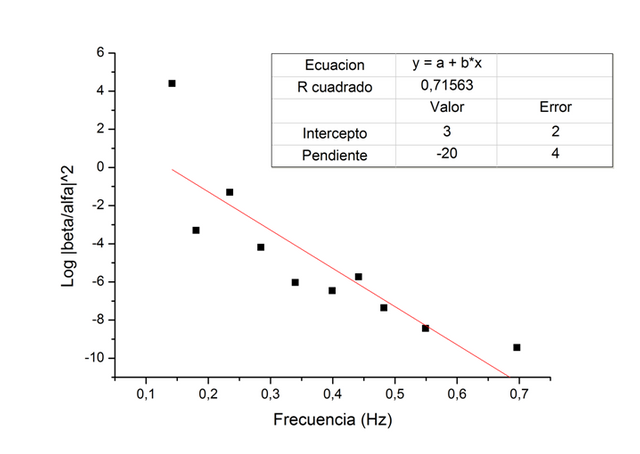
The next plot are the results that I get that "proves" the existence of the oscillations that generates Hawking radiation. Even we can find the temperature of the White Hole analogue. The explanation of how to get this plot is a very long one, and maybe I will do it in another post.
And that is all! That is how a Black Hole or a White Hole can be created in the simpler of ways, and remember: if the title says Black Hole, never it is simple .
I hope you guys that you had enjoyed this little article about a topic in which I work some months ago. I hope that now you think about Hawking radiation as a more general effect and sees the water channels in a different way.
The experiments and the channel is located in the laboratory of optics and interferometry in the Simón Bolívar university in Venezuela. I'm Moisés León, this is my first post in SteemSTEM so I hope that you like.
APENDIX 1
In fact the "disturbances" over a steady velocity in a fluid, wich we can name whit the letter delta, can be described with the following equation:
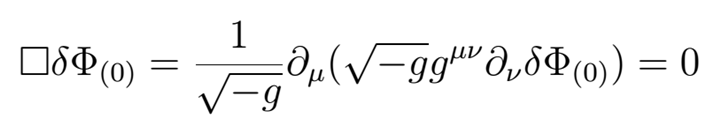
With the effective metric:
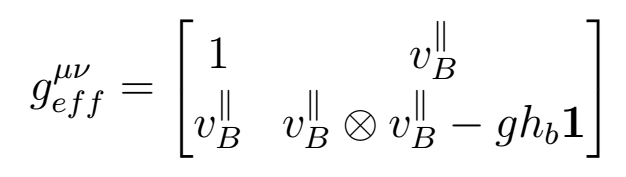
Where Delta(0) is the perturbations of velocity over the velocity Vb, which is the background velocity of the fluid, g is gravity and hb is the height of the water over a rigid floor. The wave velocity comes from the equation:
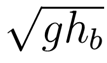
As we can see, if we make the velocity Vb equals to the wave velocity, we see the appareance of a "Horizon".
These equations has the form of the Klein Fock Gordon equation for a scalar field in a differential variety, and the metric can be transformed into the Swarchild metric with an apropiate change of coordinates.
If you are somewhat loosed, doesn't matter, this is the result of a long calculation in fluid physics. For a real understading it is better to read the original papers.
Sources:
Images:
Black Hole:
https://commons.wikimedia.org/wiki
Water waves:
https://pxhere.com/en/photo/184051
Open channel:
https://commons.wikimedia.org/wiki/
Stephen Hawking:
https://www.flickr.com/photos/lwpkommunikacio/16043158229
Hawking radiation:
https://www.quora.com/What-is-Hawking-radiation
Waterfall Images:
Bill Unruh.
The rest of the images and videos where created by me.
References
[1] W G Unruh. Experimental Black Hole Evaporation. 46(May):1351–1353, 1981.
[2] Ralf Schützhold y William G. Unruh. Gravity wave analogues of black holes. Physical Review D, 66(4), 2002.
[3] Silke Weinfurtner, Edmund W. Tedford, Matthew C J Penrice, William G. Unruh, y Gregory A. Lawrence. Measurement of stimulated hawking emission in an analogue system. Physical Review Letters, 106(2):1–7, 2011.
[4] Germain Rousseaux, Christian Mathis, Philippe Maïssa, Thomas G. Philbin, y Ulf Leonhardt. Observation of negative-frequency waves in a water tank: A classical analogue to the Hawking effect? New Journal of Physics, 10:1–14, 2008.
[5] Germain Rousseaux. The Basics of Water Waves Theory for Analogue Gravity.
[6] Rubén Rojas. Estudio de un sistema análogo a un agujero negro , con ondas de gravedad en un fluido en movimiento. Universidad Simón Bolívar, 2015.
[7] Cengel Yunus y Cimbala John. Mecánica de Fluidos Fundamentos y Aplicaciones. Mc Graw Hill, 2000.
[8] Julio Gratton. Introducción a la mecánica de fluidos.
[9] S. W. Hawking. Particle creation by black holes. Communications in Mathematical Physics, 43(3):199–220, 1975.
[10] W G Unruh. Dumb holes: analogues for black holes. Philosophical transactions. Series A, Mathematical, physical, and engineering sciences, 366(1877):2905–2913, 2008.
Usefull info
PBS SpaceTime:
wow que interesante información. se nota que aprendió en tu universidad.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Si! es un tema super interesante. Que bueno que le gustara!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @moises1692! You received a personal award!
Click here to view your Board
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @moises1692! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit