
A couple of months ago, I had watched this poetry slam single conducted at the great plains in 2014 by Dylan Garity titled My life in Prime numbers. Somehow, Dylan used prime numbers to describe how humans are gradually losing their trust for instincts and the sheer tendency to explore and dream big like children do. And how we have come to depend too much on wires and computers. Even though the poem is sparsely related to the title of my article today, at least he did point out some important facts about prime numbers, enough to make me wonder how powerful or important they are to the modern world, which led to this article. Needless to say, it was a good poem, which i think you'll find it worth your time. Happy listening at the end of this article.
Back to our Prime numbers. I did look them up, and I discovered that so much of what we create and protect, fall under the jurisdiction of prime numbers!

What are prime numbers?
According to Mark Haddon, the author of The Curious Incident of the Dog in the Night-time, Prime numbers are what we have left when all the patterns to numbers are taken away. Though logical, one could never work out their rules completely. I do agree with Mark on this one, given how unpredictable they become as we head down the number line. However by basic Wiki definition;
prime numbers are natural numbers that cannot be formed by multiplying two smaller natural numbers.
That explanation doesn't exactly give a proper insight to what prime numbers truly are. But in other words, we could say a number is called a prime number if it cannot be divided by any other number without remainder, other than itself and 1.
Some early examples of prime numbers based on the ascending order of the number line include:
Running through these numbers, we would discover that they have a few things in common. Below are some fun facts about prime numbers:
First off, they can only be divided by themselves and by one to get a quotient without remainder.
Apart from the least member 2, no prime number is an even number. Hence, one quick way to check if a number is not a 'prime suspect' is by dividing it by 2. If it gives a quotient without reminder, it cannot be a prime number.
You cannot multiply 2 prime numbers to get a larger prime number. Again, simply because each prime number is the basis of itself.
Natural numbers are either prime numbers or composites. If they aren't prime numbers, then they are composites.
Prime numbers are endless. no matter how much is found, we can never really get enough of them. just as there's no ultimate natural number.
The prime number 73,939,133 is often regarded as a weirdo, owing to the fact that if you keep removing its last digits, the answers are always prime numbers as well.
Pretty cool stuff huh?

Prime numbers in retrospect
Prime numbers are thought to have dated as far back as 1550BC when the Egyptians used symbols and markings to denote fractions, natural numbers, composites and values on the Rhind Papyrus (an old scroll where these marks were saved on.). However, it wasn't until 300BC when Greek Mathematician Euclid proved that prime numbers existed up to infinity, and that their discovery could never be extinguished.
As the years passed, more mathematicians came into the picture, and it was discovered that prime numbers left no pattern at all that could lead to the formulation of a general rule. Rather, the more these numbers were discovered, the more difficult it became to find the next one. However, the probability of finding the next one was always there, which made it quite an adventure.
Presently, the largest prime number yet discovered is 277232919. It was discovered by John Pace, a 51-year-old FED-ex employee living in Tennessee on his PC. The number contains over 23.2 million digits, and would require 9000 pages of paper to write down completely! Even though it was reported to have been discovered on 26 December 2017, it took Mathematicians and a supercomputer six (6) whole days of non-stop computing to prove its primality!
Now, even though science hasn't been able to create a single formula to find and resolve all of these prime numbers, we do have some mathematical and logical methods that help in terms of narrowing things down and sorting out 'prime suspects' from the bulk of numbers, which, still is a lot! One way science discovers and tests these numbers is the use of Primality tests such as the Fermat's little theorem which uses the expression ap-1 ≡ 1 (mod p). Where a is a non-negative integer, and P is the prime suspect. There's the Lucas-Lehmer Primality test which applies to only Mersenne prime numbers, the Pocklington-Lehmer primarity test which would require a partial factorization of N-1 to check if the number N is indeed a prime number or a composite.
Also, there is the Ulam spiral, often referred to as the Prime spiral, which is a graphical square pattern of dots that features prime numbers at the vertices of an expanding spiral square each time.
One question we should ask ourselves is: To what end? why do we need these numbers anyways? Which brings me to our discussion for the day: Cryptography.

Case Use: Cryptograghy and security!
During the early times when prime numbers where just being newly discovered, it was just for the fun and thrill of discovering and writing down these numbers rather than what they could be used for. At the time, expressions such as the Fermat little theorem was widely in use and scientists would test prime suspects for hours without success. However, after the advent of the internet some 400 years later, a few online breaches, scams and scandals brought the privacy of information and digital assets into question. Users began to realize the need for encryption and security, and what other way is there to keep information that would remain secret than trusting in the radicality and unpredictability of prime numbers?
Cryptography and prime factorization.
You see, Prime numbers often-times, are referred to as the atoms of numbers, owing to the fact that they have no even divisors except themselves -just as atoms are regarded as the indivisible units of every element.- no matter how large they are. This simply implies that every natural number can be broken down into it's most basic constituent prime factors (except the prime factors themselves, which stand on their own). The process of breaking a number down to it's most basic multiplying prime factors is what we refer to as Prime factorization.
Let's take a large number. Say; 15872, and try to factorize it into its constituent primes. Seeing that this number is an even number, it cannot be a prime number. Hence, by dividing throughout by a constant prime factor, we could reach a point where it cannot be divided any further. 2 often comes to mind as a good divisor, since it is one of the first numbers used for any primality test. Dividing by 2 repetitively yields the numbers: 7936; 3968; 1984; 992; 496; 248; 124; 62 and finally 31. It takes the number 2 nine times to divide 15892 to its basic prime number constituents, and we stopped at 31 because it is a prime number. Hence, the number 15892 can be also written in terms of its basic prime constituents as 29 x 31.
For smaller numbers such as this, prime factorization might not be such a fuss. However, it gets pretty exciting as these numbers get larger, which is exactly where cryptography comes into play.

How cryptography works. -- The Public-key Cryptosystem.
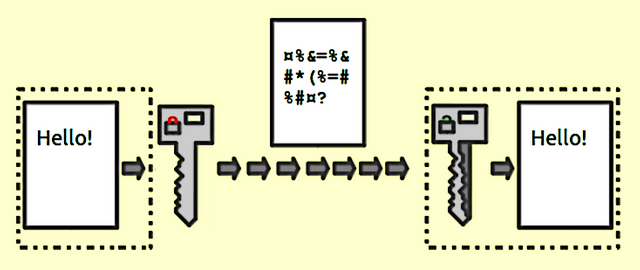
Prime factorization is the bedrock of Cryptography. It explores the tediousness of cracking (factorizing) really huge encrypted prime numbers for keeping stuff protected and safe. Currently, there exist several methods of cryptography, but perhaps none is as commonplace and as trusted as the Public-key cryptography, a relatively new method that uses a number of methods for encrypting and decrypting information.
One of the methods used in Public-key cryptography is a two-way algorithm referred to as the RSA cryptosystem or the 'Trapdoor'. It was Developed in 1977 by a 3-man team of scholars comprising Ron Rivest, Adi Sharmir, and Len Adleman. Hence, the name RSA.
The trapdoor algorithm basically deals with two functions, where it is easy to solve one function to derive the other, but it becomes extremely hard to solve backward to the first function unless some additional info is supplied.
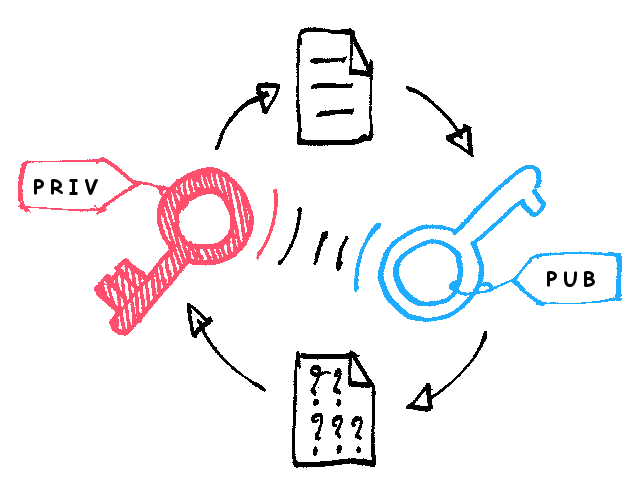
The way it works is that there are two keys required for a transaction. A public key which is owned by the sender, and a private key owned by the receiver. The public key acts as a box and hides true access to the information as well locate the receiver. Even though this 'box' might be viewed or intercepted, the information contained cannot be accessed without the use of the private key. Hence, in the RSA Cryptosystem, Information is encrypted and packed into this public key and sent to the receiver. Thus, completing the easiest and most basic side of the trapdoor. The receiver in turn, upon receiving the public key, uses the private key to solve the trapdoor in order to view and access the information in the public key. Without the possession of this extra private key, the doors stay shut!
Makes any sense? A bit? let's get practical then.
Let's say I step into a class and ask the students to solve a simple 4 x ? = 8 math. It's easy to see that we just need one digit to multiply 4 to give us 8. It's a no-brainer and the answer is 2. How about if I simply write a random large number on the whiteboard, say ???? = 2000, and ask the students to find a series of numbers that can be multiplied to get that number. You'd agree that I would have a wide range of answers, all mathematically correct ones. However, if I was already poised to choose a particular answer, then the rest of the answers, though correct, are invalid until I get the exact one I was looking for.
That is exactly how it works, but it gets even more tedious. Let's say the answers I need is restricted to just two numbers X and Y. But not just two numbers, two prime numbers! If you understood the example where I factorized the number 15872 as I explained prime factorization earlier in this post, you'd agree that one of the prime numbers would have an exponent superscript of numbers, say, abcdefgh and may likely e written as (X . Yabcdefgh ). The magnitude of the number abcdefgh would depend on how many times I had to divide the given value (which in this case, won't be much since I used 2000).
Looking at that alone, one would understand how tedious a task it would be to pick a prime number outta the blue, -which of course, should be a really big one as far as cryptography is concerned- and then take the exponent to get the answer. But hey, what if the exponent was on the wrong number all that time? What if it was on X and not Y?
Or Let's say you figured out you have no idea what those two numbers are, and you're gonna try working with what you have by factorizing 2000 to arrive at X . Yabcdefgh. Either way, these values would run in million given the fact that some prime numbers being used for encryption these days are several thousand figures long. Frankly, I don't see an easier option in any of that, and you'd sure be doing it for a very long time!
According to Scienceabc, even Super-computer testing over a million combinations per seconds would require about 10194 seconds to factorize a cryptographically encoded public key. That's literally impossible for these computers, for now, seeing that the universe is just about 1018 seconds old yet!
Hence, 2000 (our hypothetically large number) is the public key in this case and the product of the unknowns X . Yabcdefgh (which are large prime numbers) is the private key.

Some other uses of prime numbers.
Are these numbers even applied to anything else other than generic crypto-passwords and internet securities? Well yes!
Firstly, Prime factors are used in math problems to find the Lowest common multiples (L.C.M), and the Highest common factor (H.C.F).
Also, ISBN checksum codes at the back of textbooks are all prime numbers!
Prime numbers are used for detecting errors in data, in hash tables, and in PRNGs ( Pseudorandom Number generators)
The prime number 5 is used in the construction of a regular pentagon with only a compass and a ruler.

Life in numbers!
Concluding, one could be tempted to say that even life itself exists in numbers, and prime numbers, being the 'atoms' of numbers, are super-important and are applied to a lot of processes that seeks to build and develop anything in our world. Just name it; from the very ordered scale patterns on pineapples and the hexagonal structures of honeycombs in nature to basic programmes and game theories for your favourite video games, these numbers hold themselves at high regards and that would explain why early mathematicians spent decades obsessing over them.
Hence, we do hope that getting more of these numbers would provide a bigger spread of data that may help us finally identify a pattern behind it all. Which of course, would unlock lots of opportunities for even better technologies and processes in the future. The major challenge faced by number scientists is the factorization of really large prime numbers, which is basically impossible at present, even with the most sophisticated cutting-edge computing machines available. However, the word out in the street is that quantum computers are currently being developed, and might be able to solve these problems in a matter of minutes. However, they are still decades away from being completed and finally put to use. Who knows, we might see that happening in this lifetime.
Oh and, if you feel you've got some extra minutes of your time to spare, I heard the Great Internet Mersenne Prime search (GIMP), is offering a $3000 prize to anyone who discovers the next prime number. You might want to tag along on that one by signing up as a volunteer on the official website here.
Here's the link to Dylan's Poem as promised!:



Super Wavy🌊!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hala Bigwaves!!!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Prime numbers are greatly used in encryption process and the application of prime numbers in cryptocurrency is also significant. I've heard, machine developers also use prime numbers when building a machine to avoid repeating harmonics and the losses occurred by it. Your article is well explained and informative, man.
Its good to see 'Groots' caring about prime number and its functionality! xD
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
We don't get to see that everyday right? lol...
Wait, now that you've mentioned it, who knows, it could have some application as well in developing Bombs and warheads too. Say, an IED... ;-p
Thanks man, Great feedback there, i was running short of case uses.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
could be! whp doesnt want to fire an unique piece of bomb? :D
lets see if we can make a prime ied :D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Lol as his name implies right?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
The curious incident of the dog in the night time was a good read. Other than what I read in the book, didn't know prime numbers had so many applications..
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thanks buddy. fixed. And yes, prime numbers do have a wide range of importance to life.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I now know that, all thanks to you and your insightful post.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
That's a super cool one pangoli, so much about the numbers making me wonder where we will be without them, your article is an art 👍
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
A very interesting read @pangoli, thanks for your contributions!
Just wow! I can't even wrap my head around this number. MIT Professor Daskalakis once said that 2^1000 is bigger than the product of all molecules contained in the Universe and all nanoseconds since the Big Bang event. I bet you get why I find this number shockingly big!
Take care!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
It is an amazingly long one. And what's interesting is the fact that this one surpassed the previous biggest prime number by over a million digits. So who's to say what we're expecting the next one to be. Maybe five million more digits? ;-o
thanks for coming around buddy.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This explains so much and why certain things are so...
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You just explained prime numbers in English.. I'm dazzled
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hahaha... Lol..
Forget what they showed us in primary school.. This is the real deal...
You're buying pizza the next time we meet.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Wow.... I read Every word!
I learnt a whole lot: i have never really given any serious thought to prime numbers and its so fascinating how prime numbers are so important....
Great work. I look forward to reading your next post
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit