When you think of mathematics you think of equations and numbers. That's a good picture of mathematics already. The fundamental objects in mathematics are numbers so it is natural to begin with numbers.
It has been said that, “God invented the integers, all else is the work of Man.”
Integers should actually be whole numbers. They are a natural constructs – they are the numbers we use to count. 1 sheep , 2 sheep, 3 sheep, 20 cherries ..

Wait, what is a set?
A set is a list of objects or elements. We have a set of cards, a set of books, a set of things we love, a set of things we hate, and we have a set of friends. Some sets have finite number of objects in it, other sets have infinite number of things - so we satisfy ourselves by listing enough of the elements until the pattern become clear and write dot dot dot.
Think of it this way – mathematicians are normally lazy and so they write stuff in short notations. These notations are formalized to avoid confusion with other mathematicians.
As I start elucidating some mathematical nuggets, you’ll realize that mathematics is just basic human language converted into quantifiable notations.
What is meant by the “all else” that humankind is responsible for?
Let’s look at the different types of “number” that exist in the mathematical universe:
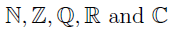
Respectively: the naturals, the integers, the rationals, the reals, and the complex numbers.
It obvious where the N, R, and C comes from if you are an English speaker. The Z and Q are questionable. The Z comes from the German word zahlen which means “to count”. The rational number is denoted using Q for “quotients”, as you will see later.
Description of each set:
- Integer Numbers – the set of natural numbers with negative of naturals and zero
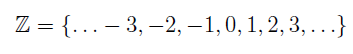
- Rationals Numbers - a set of fraction built out of integers
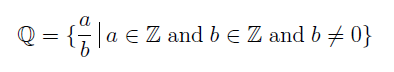
You might not be familiar with the bar after the fraction but it’s actually simple. We will digress a little bit to introduce set builders. It reads as,
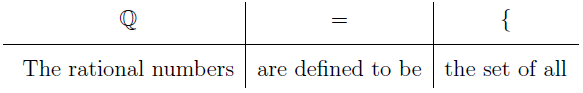
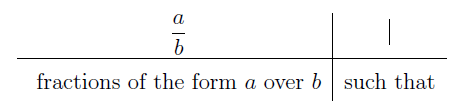

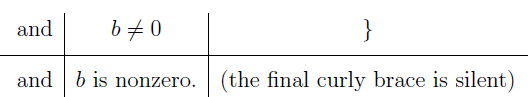
Okay, now we read it again,
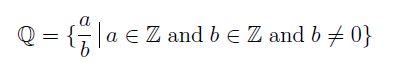
“The rational numbers is defined to be the set of all fraction of the form a/b such that a is an element of the integers (Z) and b is an element of the integers (Z) and b is not zero.”
There you have it; you can now parse mathematical equations into its equivalent English translation. Mathematical notations represent a huge improvement with regards to brevity.
that escalated quickly
Forget that Standard Model equation for now. Let’s continue with our sets of numbers …
- Real Numbers: the actual definition of real number is extremely difficult, but an intuitive description, a real number is a number that measures a physical quantity.
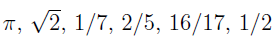
In some textbook, it is defined to be the union of rational and irrational numbers. We’ve encountered rational number, but irrational – what is this beast?
Irrational numbers are numbers that can never be expressed as a fraction a/b where a and b is of integers. Pi is the best example of this irrational number.
- Complex Numbers – is define to be of the form
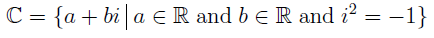
Let’s parse it again in English translation.
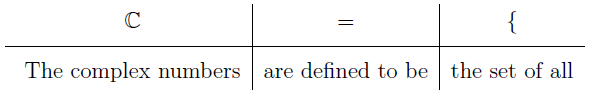
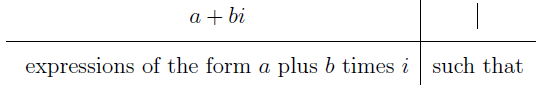

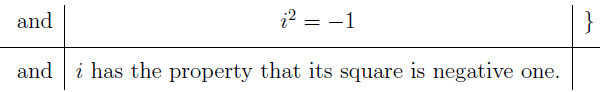
Sometimes complex numbers are denoted with Greek or Roman letters.
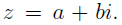
We introduce some operations to extract the real and imaginary parts of z.
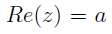
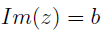
Conclusion:
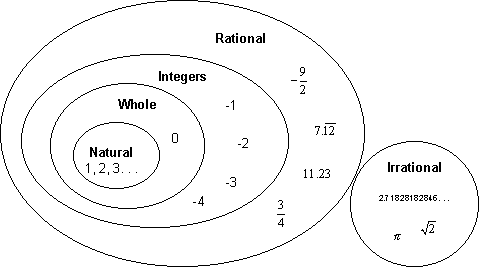
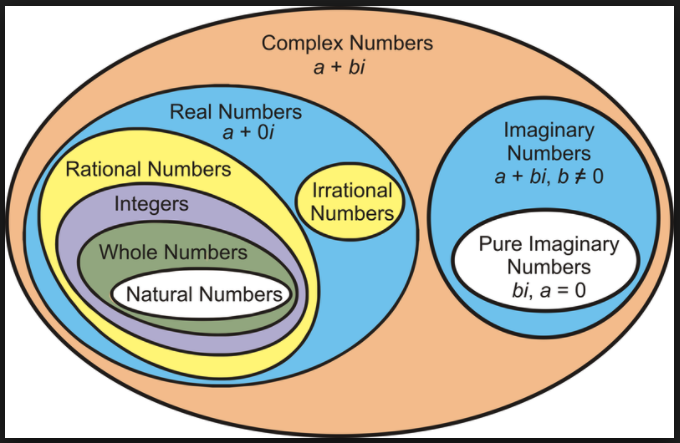
In summary, you can picture mathematics as a theater play with different actors being N, Z, C, Q, and R. Each has its role each has its own skills and somehow they are interrelated to each other.
Natural numbers are contained in integer, an integer is contained in rational numbers, and rational numbers are contained in real numbers, and all real numbers are contained in complex numbers. Refer to the image below for visualization.
It's a really nice post.....especially for those who are struggling with maths it would be very helpful...thanks for sharing.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Your welcome.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Bringing it down to the lowest standard anyone can understand... Pretty Nice work.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Quick question, what's the difference between intigers and whole numbers/ whole numbers and intigers!??
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Think of this way, first you have natural numbers - the numbers we use for counting physical objects, like 1,2,3,4, etc. Then introduce the idea of "nothingness" using zero and incorporate that into your set of natural numbers, we now have 0,1,2,3, etc. We now have a set of whole numbers.
Then add an idea of its anti-number such that any number added to that anti-number results in nothingness or zero. This anti-numbers union with the whole numbers gives us the integers.
Summary:
natural numbers: 1, 2, 3, ...
whole numbers: 0,1,2,3,4,
integer numbers: ...,-4,-3,-2,-1,0,1,2,3,4,...
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Ahh gotcha!
It was the inclusion of 0 in whole numbers that had me confused! Thanks for clarifying! :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has received a 26.32% upvote from @msp-bidbot thanks to: @sinbad989. Delegate SP to this public bot and get paid daily: 50SP, 100SP, 250SP, 500SP, 1000SP, 5000SP Don't delegate so much that you have less than 50SP left on your account.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You got a 1.08% upvote from @bid4joy courtesy of @sinbad989!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit