In my last post I have talked about the use of radiogenic isotopes in geology. Here I would like to expand on that and talk more in detail about the field of geochronology.
Geochronology is based on the assumption that radioactive parent isotopes decay to daughter isotopes during constant radiogenic decay. Depending on the age of the material that we wish to date, we need to choose a system with a fitting half life.
For example:
If we want to date crust forming processes that lasted billions of years, it is not useful to use radioactive carbon (14C) for that purpose. The half-life of 14C only measures 5730 years. Therefore, very old rocks will just have no measurable radioactive carbon left to measure. On the other hand you will not be able to date tree rings or quaternary volcanoes with the Sm-Nd-method that has a half life of 106 billion years. In timespans as short as those no measurable daughter isotopes would have formed yet.
The general rule is:
For geochronology you should use a system that has a half time between a thousandth to ten times the age of the material that you wish to date.
It is also important to choose a system of elements that is incorporated in the material that you wish to date in sufficient quantities.
At last, in addition to the appropriate half-life and the concentrations, you need to consider what exact moment you are dating and how it is geologically relevant.
The radiogenic decay of a parent isotope with the starting amount of N0 can be described by
Where λ is the decay constant and t is the time. During radiogenic decay of an isotope the daughter isotope will enrich. Because the of daughter isotopes born is always equal to the amount of parent isotopes decaying we can write
Which also means:
At last we have to take into account the amount of the daughter isotope that has already been included in the rock. This leads us to the formula
If we want to solve for t, we obtain the formula that describes basically the complete field of geochronology:
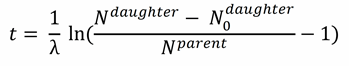 .
.Nparent(t) as well as Ndaughter(t) are measurable in the rock, N0daughter and t are unknown.
We are stuck with a formula with two unknown variables. This leaves us with a mathematical problem that has a very elegant solution, once we realize that the formula mentioned above
is nothing but a linear equation
where y = Ndaughter, a = (eλt – 1), x = Nparent, and b = N0daughter.
A line is defined by two points. If you know those two points you can calculate (or read off) the slope and the distance on the y-axis. These two are our unknown variables!
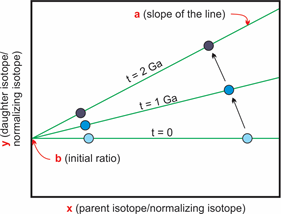
Diagram showing the isochrone method for geochronology. The older the rock, the more of the parent isotope decays and the more of the daughter isotope is present. This effect is more pronounced at high isotopic ratios, leading to the characteristic changes in the slope of the regression line. Modified after Rollinson (1993) and Markl (2008).
This means that we always need at least two minerals we can analyze or one mineral and the whole rock analysis, if we do not know the starting amount (initial value) of daughter isotopes. It is important that the two points are significantly different in their own daughter isotope to stable isotope ratio to get a good line of best fit. If the points are close together the error on the slope of the line gets larger.
The line that is created by the connection of different points of measurements for the same age is called isochrone.
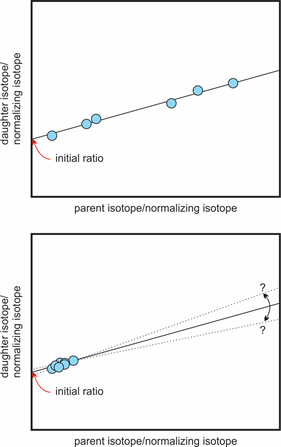
Difference between a well-defined isochrone (top) and a poorly-defined one (bottom). Modified after Rollinson (1993) and Markl (2008).
In certain minerals only the parent isotope is built into the crystal structure (Uranium in zircon, K in potassium feldspar). We can therefore assume that all daughter isotopes in those crystals have been formed due to radiogenic decay since their formation. In those cases we are able to measure an age for a single crystal.
References
- Faure, G. and Mensing, T.A. (2004). Isotopes: Principles and applications (3rd edition): New York, John Wiley
- Markl, G. (2008). Minerale und Gesteine, 2. Auflage. Spektrum Akademischer Verlag
- Rollinson, H.R. (1993). Using Geochemical Data: Evaluation, Presentation, Interpretation. Longman Scientific and Technical.
Being A SteemStem Member
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
You received a 80.0% upvote since you are a member of geopolis and wrote in the category of "geopolis".
To read more about us and what we do, click here.
https://steemit.com/geopolis/@geopolis/geopolis-the-community-for-global-sciences-update-4
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
I like this post but you haven't sourced your photos exactly (not looking into your references at this time) and it takes away from it.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for pointing that out. I could not find any suitable diagrams online so I drew these ones myself. But I have included the textbooks after which the diagrams were modelled now.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Okay, sorry! Thanks for letting me know
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit