In 2008, the construction of the Large Hadron Collider, or LHC, was completed. At the same time, I visited CERN, where I was offered a tour of the main experimental installations of the LHC. Before that, I usually participated only in the CERN conferences, but the tour of the working settings made an indelible impression on me. The experimental setup was called the "compact muon solenoid". It was quite small, by the standards of CERN, a device as large as a three-story house, and I witnessed the final assembly of all its components. Massive cone-shaped gizmos were placed inside the barrel-shaped detector housing - all this resembled a lot of giant digital cameras, the lenses of which were facing the center of the detector, where high-energy proton beams collided.
At the end of the tour, we climbed a little on the French Alps: nothing difficult for a good climber. I managed to get to the top of Aiguille du Midi and found that there was a ropeway down there, along which my colleague and I went down to the small town lying at the foot of the mountain. The range on which we climbed is characterized by dense traffic, despite the fact that the path is very narrow and covered with snow. For some reason, all climbers prefer to climb it in a bundle, although it always seemed to me that the ascent partner is not a very reliable anchor. In the case when one of the partners breaks down, the other has to put a lot of effort to stay on his feet and not fly away after the friend. I do not like to walk in a bunch, and I prefer, when climbing, to rely only on the strength of the hands and on the hammered hook. Nevertheless, I must admit that my colleague and I performed this climb in a bunch, like everyone else: my partner was a very experienced climber, and the ridge did not look difficult to pass.
Now, in retrospect, I think that climbing along a narrow ridge can serve as a successful metaphor for a story about the Higgs boson, in the hope of discovering which (among other things) the LHC was built. Imagine that you are standing on the narrow crest of the ridge, with difficulty maintaining balance. Step left, step to the right - and you fly into the abyss. In the same position, there are tachyons in string theory: they balance in an extremely unstable equilibrium, and the slightest indignation sends them to a fatal fall down the slope. But that is not all. Imagine that eight mountaineers walk along the ridge and one of them loses balance and falls to the left. The second is experiencing a pull of the rope, knocking him down, and falls after the first - also to the left. The third, praying with a request to help him keep the weight of two fallen comrades, is preparing to follow them.
The only thing that can be done in such circumstances is to jump from the ridge to the right and pray that the rope does not fail. But for a number of reasons, this is difficult to do. Let us return to the tachyons and to the Higgs boson. Tachyons show instability in any point of space, and this phenomenon is collective. Tachyons are like a group of climbers walking in a bunch. If one tachyon loses its balance and begins to slip into the abyss, it carries with it nearby "comrades".
The Higgs boson was invented to describe a tachyon condensate. Tachyon condensation is a term describing the process of stowing tachyons from the ridge to the valley. Imagine that climbers who have fallen from the ridge do not die to death, but miraculously escape and gently land in the valley. There they have a "Club of fallen climbers". They are tired after a hard climb and do not have the strength to climb back up the mountain. Instead, they roam the whole crowd along the slope, periodically one of them tries to climb the slope, but slides back. Tachyons, condensed at some point in space-time, behave approximately the same way: the quantum fluctuations of the tachyon condensate are the Higgs bosons.
source
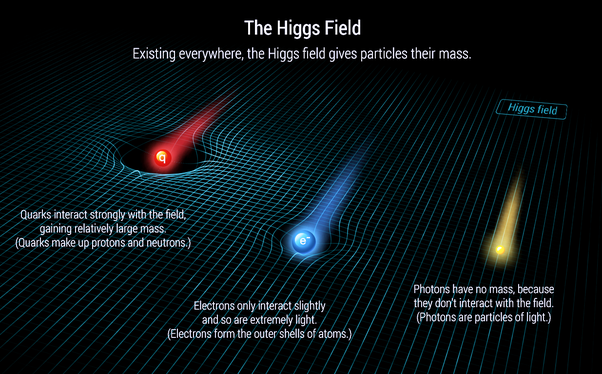
The difference between the behavior of the Higgs boson and the behavior of the members of the "Club of Fallen Climbers" is that the movement of the Higgs boson does not occur in the ordinary four-dimensional world, but in additional space-time dimensions. Despite the fact that the Higgs boson for a long time maintained the status of a hypothetical particle, it serves as an illustration of a well-developed physical theory, perhaps the best of all that was invented in the last decades. This theory is called the Standard Model. The word "standard" in this case means that this theory is universally recognized, and the word "model" indicates a preliminary, incomplete character of the theory. The standard model is not limited to the description of tachyon condensate. Among other things, she explains the role of the Higgs boson in the formation of masses in subatomic particles: electrons and quarks.
In 2010, a one-percent difference in the number of muons and antimuons formed during the decay of a heavier particle was detected in experiments with an elementary particle accelerator, called Tevatron, which was an indication of the existence of the Higgs boson. It was expected that experiments at the Large Hadron Collider would help confirm or disprove this hypothesis. It should be noted that two decades earlier in Texas it was planned to build a superconducting super-collider for these purposes, but in 1993 Congress pulled the project financing plug from the outlet of the state budget, saving US taxpayers ten billion dollars, thanks to which the United States lost its leadership in the field of high-energy physics to the old Europe , and on July 4, 2012, CERN reported with great pomp about the long-awaited discovery of the Higgs boson ...
source
So, what is supersymmetry? Supersymmetry operates with additional dimensions in a rather peculiar way. Measurements that we normally operate, including additional ones, form a metric space, that is, a space with a measure, or simply a distance. The distance is a number: 2 centimeters, 10 kilometers, etc. If you add two distances, the result will also be the distance. When multiplying two distances, we obtain the area. But the additional dimensions that supersymmetry operates on are not expressed by numbers - at least, by ordinary numbers.
They are expressed by anticommutative numbers, which are the cornerstone of the strange mathematics of supersymmetry. The anticommutative numbers play an important role in the description of electrons, nucleons, quarks, and other particles called fermions. Despite the fact that I have not yet defined the terms "anticommutativity" and "fermion", I will still use them, just to call things by their names, without going into the jungle of very complex mathematics. Additional supersymmetry measurements are called fermion measurements.
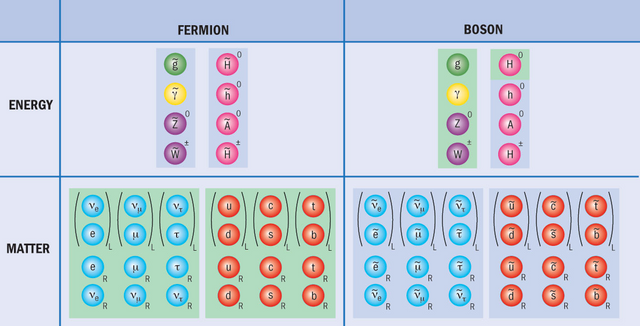
Fermion measurements, in contrast to the usual ones, imposes a number of restrictions on the nature of possible motions. A particle can move forward or backward in the fermion measurement or rest, but when moving it can have only one fixed "velocity". True, speed is a very crude analogy for describing the motion in a fermionic measurement. Much better for such a description the concept of spin is suitable. You remember that many particles have spin, that is, roughly speaking, they rotate, however, the speed of this rotation can take only fixed values. The electron has a minimal nonzero spin. A photon has a double spin, than an electron, but, as we already know, the spin of a photon is always oriented in the direction of its motion. Graviton has twice as much spin as a photon. And it's all. There are no fundamental particles whose spin is greater than the spin of the graviton. If the theory of super symmetry is correct, then the Higgs boson does not move in any of the fermion measurements.
The electron moves in one, the photon in two fermionic measurements. As for the graviton, it all depends on how many fermionic measurements are at its disposal. It may be, for example, that part of the spin of a graviton is due to fermionic measurements, and a part to ordinary space-time measurements. Fermionic measurements have one exceptional feature, which is expressed in the so-called principle of prohibition. The principle of prohibition was formulated in 1925 by Wolfgang Pauli, and it says that two fermions can not simultaneously be in the same quantum state. Electrons are fermions, so two electrons in a helium atom can not be on the same orbit in the same state - they must at least have oppositely directed spins. Fermions are by definition such particles that obey the principle of prohibition.

source
Particles that do not obey the principle of prohibition - and include photons, gravitons, gluons and the Higgs boson - are called bosons. The behavior of bosons is radically different from that of fermions. Bosons not only can be simultaneously in the same quantum state, but more than that - they prefer to do it. Supersymmetry establishes the relation of partnership between bosons and fermions. Each boson supersymmetry puts fermion into partnership, and vice versa. For example, the Higgs boson as a supersymmetric partner has a fermion, called a Higgsino (sometimes it is also called a "spike"). Whatever we call it, the Higgsino is nothing more than a Higgs boson moving in one of the fermionic dimensions.
The key idea is that fermionic measurements are a mathematical abstraction. They are nothing more than the algebraic rules used to describe them. Supersymmetry is the symmetry between bosonic and fermionic measurements. What does this mean? Symmetry in the broad sense is the immutability of something under certain transformations of this something: for example, the symmetry of a square means that when the square is rotated by 90 °, we get exactly the same square. Boson measurements are ordinary measurements such as length and width. Six additional measurements of string theory are also bosonic measurements, but they do not interest us now. Fermion measurements are just a set of unusual algebraic rules.
By analogy with the rotation of the square, we use the term "rotation" for the supersymmetric transformation. A rotation from a bosonic measurement to a fermionic one means that if the particle moved in the bosonic measurement before turning, then it does not move in the boson measurement after the rotation, and vice versa, if the particle did not move in the boson measurement before the rotation, then after the rotation it starts moving in it. Unclear? Well, I'll try differently. Physically, this means that if we take a boson, then after turning into a fermionic measurement it will become a fermion. Mathematically, a supersymmetric rotation from a bosonic measurement to a fermionic measurement means the replacement of the number 1 denoting the boson measurement by one of the letters a or b, which denote fermion measurements.
The preservation of the object's invariance under a supersymmetric rotation reduces to the fact that the resultant fermion will have the same mass and the same charge as the original boson. And this leads us to one of the most fundamental predictions of supersymmetry: for each boson there must exist a supersymmetric partner: a fermion with the same mass and charge, and vice versa, for every fermion there must exist a supersymmetric boson. One of the facts we are sure of is that the world is not perfectly supersymmetric. If in this world there was a boson with the same mass and charge as an electron, we would undoubtedly have known about it, because the existence of such a boson would radically change the structure of the atom. Perhaps there is some mechanism, similar to the mechanism of condensation of tachyons, which violates c> persimme trium. If the idea of the existence of this strange new symmetry makes you feel like walking on quicksand, it's not my fault. Like most of string theory, supersymmetry is the product of a long chain of speculative theorists' arguments and does not have reliable experimental support.
If the hypothesis of supersymmetry and fermion measurements is confirmed experimentally at the Large Hadron Collider, it will be a triumph of pure reason - a rematch for all the previous ridicule of skeptics. However, it is possible that skeptics will be right. Frankly, I will not be surprised at any outcome.

References:
1, 2, 3 and 4
Support @steemstem and the #steemstem
project - curating and supporting quality STEM
related content on Steemit




many thanks for the info @techlife
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit