The Humble Pie Chart: How to Use, But not Abuse

_{Image source: see note at end of post}

Many visualization experts recommend that you avoid using Pie Charts, but the evidence shows that when used appropriately, pie charts can be as effective or even more effective than the alternatives--usually some form of bar chart. This evidence is nicely reviewed by Spence in No Humble Pie: The Origins and Usages of a Statistical Chart. In this article, I will focus more on using examples to illustrate the strengths and weaknesses of pie charts and their common alternatives.

Purpose: Analyzing Part to Whole Relations

Pie charts are designed for visualizing and analysing part to whole relationships: how the parts of a whole relate to each other and to the whole. For instance, suppose you want to know how the total sales in each of three regions relate to overall total sales and to each other, such as:

Given this data, you might want to answer a few different types of questions that are typical of part to whole analyses:

• What is West's proportion of total sales?
• What region has the highest proportion of sales?
• Of the Central and East region, which has a bigger proportion of sales?

Of course, you can answer these questions using the numbers in the table above, but the point of visualization is to make it easier to answer these questions by harnessing the power of visual perception.

Let's walk through each of the types of questions above, comparing pie charts to some alternatives.

What is a Part's Relationship to the Whole?

For these charts, consider answering the question: "What is the percentage of total sales of the West Region?"

Many experts suggest visualizing part to whole data as a bar chart showing the percent of total. In the chart below, I intentionally removed the numerical legend, because I want you to focus on the analog representation of the data: the heights of the bars, not a digital representation using numbers. In an analog display, visual features change in proportion to the data they represent: a greater number translates to a taller bar. With a digital representation greater numbers do not always translate this way: 7,000 and 6,999 are completely different visually, even though the data they represent differs only by 1.

Given this bar chart, can you determine the percentage of total sales in the West region?

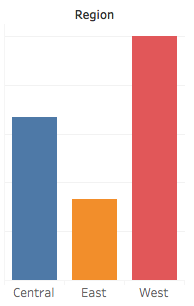
Now try to make the same estimate of West's proportion based on this pie chart:

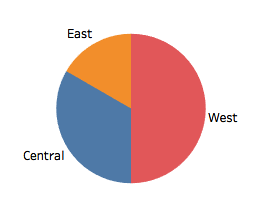
In the pie chart it is easy to see that the West region makes up 50% of total sales. In the bar chart however, this is harder to see--you have to stack the Central and East bars up in your mind's eye to see that together they are about the same height of the West bar. Even then you are probably thinking "West is about equal to the sum of the other regions", not "West is 50% of the total."

The pie chart has other advantages over the bar chart. First, it is very obvious that it represents parts of a whole. This is not at all clear in the bar chart without additional information, such as a Y axis with the title "Percent of Total Sales". Even then, the chart need not show all of the regions, so the user is left to estimate each bars proportion to ensure that it all sums to 100%.

The second advantage of pie charts is that many viewers are very familiar with them. The charts are commonly used in the media, plus fractions are often taught using pies. As a result, many viewers intuitively get the pie chart.

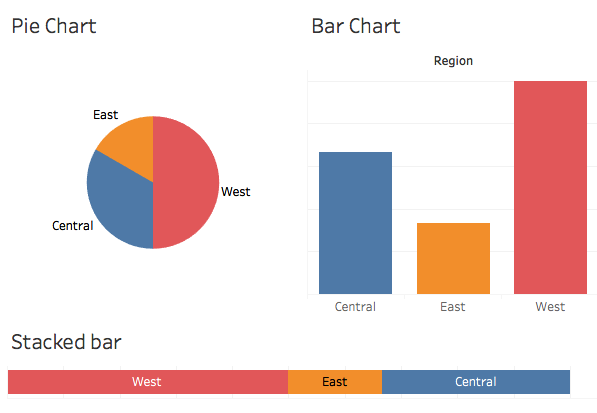
Another alternative to the pie chart is the stacked bar chart:

As with the bar chart above, it is not immediately obvious that this represents parts of a whole. However, once you know that, unlike the bar chart, it is somewhat easier to see that West is 50% of the whole. Ask yourself though, whether it is easier to see this using the pie chart or stacked bar chart.

Which Part has the Highest Proportion?

Now look at the three charts below and ask yourself which graph seems easier to use to determine which region has the biggest proportion of sales:

With this data, all of the charts work well. However, consider charts for a slightly different data set:

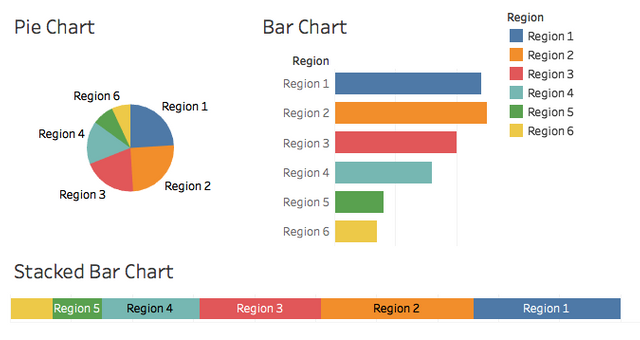
With the pie chart it looks like Region 1 or 2 might be the biggest, but it is somewhat difficult to tell. However, the bar chart clearly shows that Region 2 is the biggest. This is because it is easier to compare the length of the lines since they share a common baseline. The stacked bar might be a little bit better than the pie chart, but it is still difficult to be sure of the bigger region.

Sorting from high to low can help if the user recognizes that the pie wedges or bar segments are sorted, but it can still be difficult to tell whether two consecutive items are different or equal:

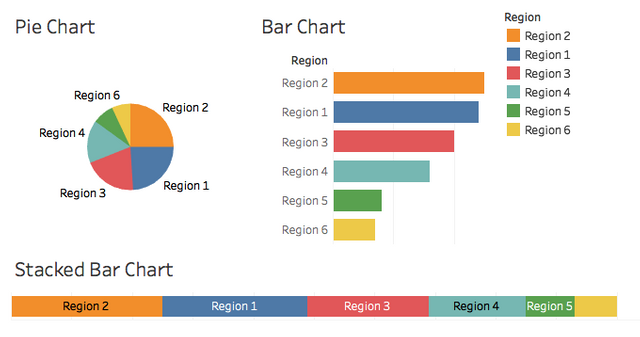
There are still more issues here with the pie and stacked bar charts:

• Smaller proportions are even harder to discern and compare. Look at Regions 5 and 6. The smaller the region on the display the less screen resolution available to represent an actual difference.
• It is often not possible to label all of the elements, necessitating a legend. This requires the viewer to scan back and forth between the legend and the colored segments.

Which of Two Parts is Bigger?

This question is similar to asking which has the biggest proportion of the total, but can be much harder if you are asked to compare two very similar parts that are very close in value and very small in the display, such as regions 5 and 6 above. Even though you can clearly see that Region 5 is bigger than 6 in the bar chart above, even bar charts can suffer from this problem when one or more bars are a lot bigger than others:

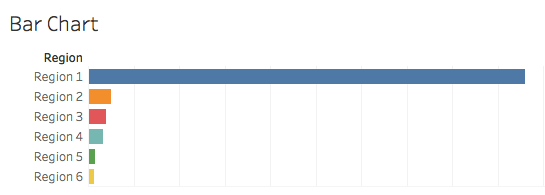
However, even above when I multiplied Region 1's sales by 20, you can still just discern a difference between Region 5 and 6. Compare the bar chart to the pie chart of the same data:

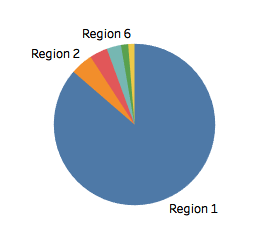
Conclusion

Despite calls to never use pie charts, the evidence shows that they are sometimes equal to or better than bar and stacked bar charts. Their advantages include:

• Obviously convey part to whole relationship
• Viewer familiarity
• For some data, just as good at comparing parts and determining part to whole as bar charts.
• Spence also reviews evidence that they are better than bars at comparing A+B to C+D, that is the sum of two parts to the sum of two other parts.

However, to get the most from pie charts, it is best to use them only when you have a few parts that differ enough so that the differences are clearly visible on the chart and there is enough space to label each segment.

It is also good to sort the segments from high to low, such as I have done for most of the charts above.

Remember that when displaying quantitive data as graphs we are often not trying to convey very precise information, but rather give an overall view of the data that makes some questions easier to answer, often at the expense of making others harder. The fact that it may not be easy to decide which of two very similar parts is bigger, or the exact percentage of a part is often not important. When that much precision is needed, a table of the actual totals, percentages, and even differences is actually better. No display of data, graphical or tabular, is best for all information questions.

Note on the Pyramid Pie Chart: There are many different versions of this chart on the internet without any clear source of attribution. I created the version above using Mathematica.

Todd

Proud member of: