~ Introduction ~
Everyday we come across mirrors or similar reflective surfaces and we take it for granted because we are used to seeing them. But why are some surfaces reflective and others not? Could it be the smoothness of the surface itself? Well I could argue it plays a certian role but we have all seen smooth pieces of wood or plastic which surely aren't reflective as a mirror is. So if it isn't purely a question of smoothness of a material, what could be the answer?

Fig1: Reflective sphere
I have thought about different approaches to explaining this "phenomnena" and I have decided to give two explanations:
- a short, purely descriptive explanation where you will need to take some things for granted and just believe me (skip all the way down to Short answer)
- one more detailed and mathematically complex explanation where we will need to cover certian calculus theorems and physical laws
Both of these explanations result in powerful conclusions which in return give us the answer to why some surfaces are reflective and others are not, but first of all we need to set some basic principles and realise what we are actually dealing with when talking about mirrors. Don't get me wrong. I'm not saying that only mirrors are reflective - I can easily see my reflection on water surfaces or turned off smartphone screens, etc... But these reflections are usually dark and not very clear as opposed to images mirrors and similar sufraces produce.
~ Light ~
We are all familiar with the basic concepts of light. We can see during the day because the Sun is shining light down on us, but if there is no light, well... then of course we can't see. Our eyes are complex light detectors and every colour our eyes can detect belongs to the visible part of the "light spectrum". More generally, light is a electromagnetic wave and the visible part of it is just a small fraction of the whole electromagnetic spectrum. It is important to keep in mind that light also shows a wave-particle duality but I will mostly be interested in its wave form.
So what is a "wave"? One of the most common descriptions of a wave describes it as a disturbance of a continuous medium that propagates with a fixed shape at constant velocity, and there are two types of waves:
- Longitudinal - particles in the medium oscilate parallel to the direction the wave itself is propagating.
- Transversal - particles in the medium oscilate perpendicular to the direction the wave itself is propagating.
Fig2: Difference between two types of waves
Waves propagate energy - for example you can generate waves on water surface by throwing a rock. These waves are a combination of the aformentioned two types and they propagate mechanical energy. As we all know these waves can cause extreme damage if they are high and fast enough.
I would now like to introduce a little bit of mathematical notation used to describe these waves in space and their evolution in time. The general linear partial differential equation of second order which describes a wave propagating in the z-direction is given by:
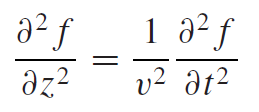
Eq1: Classical wave equation
where "v" represents the speed of propagation, "z" direction of propagation, "t" time and where "f" is a funciton of the form:
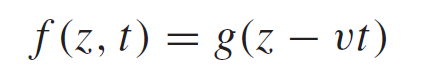
Eq2: A general wave form
This is the most general way a wave traveling in z-direction can be described. In case of a sinusodial wave (Figure 3) this wave function "f" can be written via trigonometric functions sin(), cos() or even their combination.
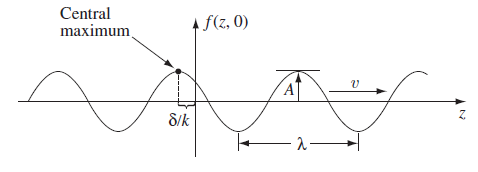
Fig3: Sinusoidal wave. Source: ref [1]
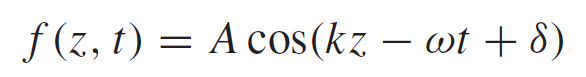
Eq3: Trigonometric wave form
Some new variables were introduced in equation 3. The wave number "k" is related to the wave lenght in such a way that when "z" advances by 2π /wavelenght, the cosine executes one complete cycle. "A" represents the amplitude of the wave and "omega" represents the angular frequency and is related to ordinary frequency of the wave. The Euler's formula allows us to introduce the complex notation of a wave given by:
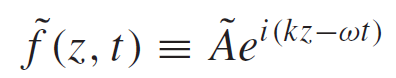
Eq4: Complex wave function - Planar wave
where "i" is the imaginary unit and where any value with tilde is a complex value or function.
Equation 4 is the most useful way of mathematically describing waves, atleast for planar light waves propagating in z-direction. I will be using this wave formulation from now on.
Let me jump back to light for a second. I stated that a wave is a disturbance of a continuous medium that propagates with a fixed shape at constant velocity but we know that light can propagate through the emptiness of vacuum. We can see stars at night but the question is how... How can this be? How can a wave propagate through nothing at all? What is this medium that light seems to "disturb" in order to propagate? Well that is a long but interesting story about the idea of universal Ether which was debunked in the early 20th century - but I will leave this for some other time. For now it is enough to say that light is a "special kind" of wave - it doesn't need a medium to propagate in. That is partialy where the wave-particle duality of light comes into play.
~ Additional mathematical notation ~
In further analysis we will need a little bit of differential calculus but I won't go into too much detail. I just want to cover some basic concepts and not how we can come to them.
I want to begin with the use of nabla differential operator which allows us to write seemingly complicating formulas into more compact forms.
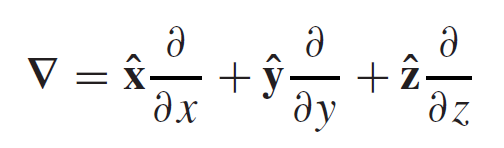
Fig4: Nabla operator in Cartesian coordinates
It consists of first order derivatives by spatial coordinates where each derivative is coupled with its unit vector. For example, let "T" be some scalar field representing room temperature. "T" being a scalar field meens that every point in space (in this imagined room) has its own value T(x,y,z) -> a scalar value for example 22 degrees Celsius. If we use the nabla operator on this scalar field "T" we get:
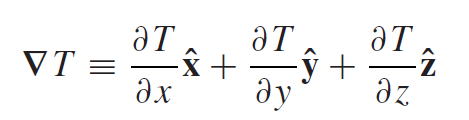
Eq5: Gradient of T
We call this the gradient of "T". The gradient is a vector quantity which points in the direction of fastest change in "T"!
Now imagine we have some other field "v". Let "v" be a vector field, for example representing speed of water flow in some imagined pipe. Each point inside the pipe has its own little vector quantity v(x,y,z) - speed of that bit of water.
Since both nabla and v are vector quantities we can multiply them in two ways: dot product or cross product. The first one gives us:
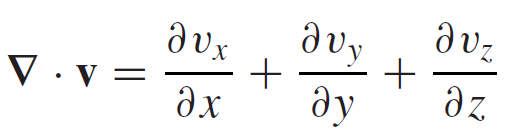
Eq6: Divergence of v
We call this the divergence of "v". The divergence is a scalar quantity which is a measure of how much the vector "v" spreads out (diverges) from the point in question.
The cross product gives us:
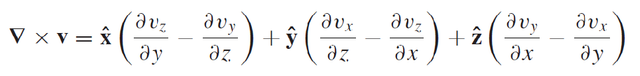
Eq7: Curl of v
This one looks really ugly but it's really only importatnt to know the basic concept of curl. It is a measure of how much the vector "v" swirls around the point in question.
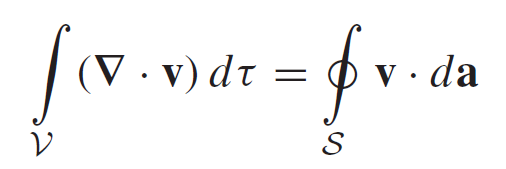
Eq8: Gauss’s theorem
The Fundamental Theorem for Divergences or more often called the Gauss's theorem states that the integral of a derivative (divergence) over a region (volume V) is equal to the value of the function at the boundary (surface S that bounds the volume).
If v represents the flow of an incompressible fluid,
then the flux of v is the total amount of fluid passing out
through the surface, per unit time. Now, the divergence measures the “spreading
out” of the vectors from a point—a place of high divergence is like a “faucet,”
pouring out liquid. Sourse: ref [1]
For example... If we have a faucet inside some volume V than the water coming out of the faucet (water being "created" in volume V) is the same as the amount of water leaving the border of volume V (if we suppose that water is incompressible).
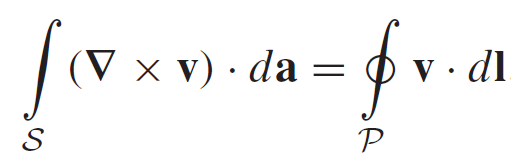
Eq9: Stokes' theorem
The Fundamental Theorem for Curls or more often called the Stokes' theorem states that the integral of the curl over some surface (the flux of the curl through that surface) which represents the “total amount of swirl,” can be determined just as well by going around the edge of that surface and finding how much the flow is following the boundary.
These theorems (and a few more subtleties) will allow us to manipulate Maxwell's equations into something more tangible and more relevant for uncovering why mirrors reflect so much light and so many colours.
~ Maxwell's equations ~
Maxwell's equations are a set of four partial differential equations that encompass the field of classical electrodynamics as a whole. In theory they are (along with Lorentz force law) containing everything you need to dissasemble and understand electromagnetism and light itself.
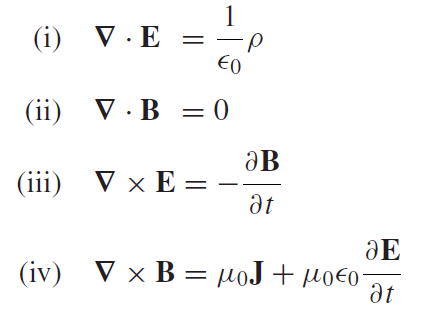
Fig5: Differential form of Maxwell's equations in vacuum. Source: ref [1]
First Maxwell's equation (called Gauss's law) togehter with Gauss's theorem states that the total flux of an electric field "E" through enclosed surface S is solely determined by the total enclosed electric charge "q" (in the right side of equation (i) the greek letter rho represents the charge density).
Second Maxwell's equation together with Gauss's theorem states that the total flux of an magnetic field "B" through enclosed surface S is always zero which means that there are no magnetic monopoles. Imagined magnetic monopole could produce such a magnetic field "B" which would "escape" from some volume and never return. Second Maxwell's equation states that any magnetic field lines that exit the surface must return and reenter thus canceling the total flux.
Third Maxwell's equation (called Faraday’s law) together with Stokes' theorem states that a changing magnetic field "B" induces a circular electric field "E" connecting the two fields.
Fourth Maxwell's equation (Ampère’s law + Maxwell's correction) states that a magnetic field "B" can be created by some arbitraty electric current given by the current density "j" and/or by a changing electric field "E"
Figure 5 represents Maxwell's equations in vacuum with a occasional local electric charge density or electric current. But in reality we mostly deal with materials of all sorts.
Some external electric field can act upon a electric charge by the electrostatic force proportional to the charge itself and the "strenght" of the field. Positive electric charges are pushed in the direction of a electric field, and negative electric charges are pushed in the opposite direction of the field. Since all atoms are made of positive core and negative electron cloud than exposing these atoms to external electric fields can pull the positive core to one side and the negative electron cloud to the other. This is called an induced electric dipole and it creates its own electric field. Since there are millions and millions of atoms in any material, these effects are not negligible. This effect is called polarization.
Similar thing applies for magnetic fields. Each and every atom with unpaired electrons has its own magnetic moment which arises from electrons spin. If all electrons are paired that the effect is a little bit different but its results are similar. In a external magnetic field, these magnetic dipoles align (anti)parallel to the external magnetic field thus changing it. This is called magnetization. As a result of magnetization, there are two effects. Paramagnetism (parallel to the external magnetic field) and diamagnetism (antiparallel to the external magnetic field).
Without too much detail I wanted to show that if we are dealing with electric and magnetic fields in materials then these materials alter the original fields. If the effects of polarization and magnetization are taken into account that new fields can be defined to allow us to rewrite Maxwell's equation in more compact form which applies to electrodynamics in matter.
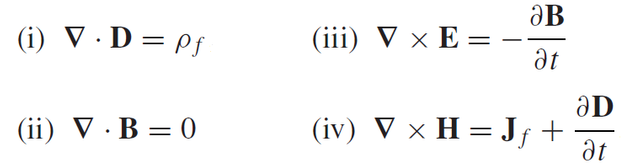
Fig6: Differential form of Maxwell's equations in matter. Source: ref [1]
"D" hides away the original electric field "E" plus the effects of polarization and is called the electric displacement.
"H" hides away the original magnetic field "B" plus the effects of magnetization and is often called "true" magnetic field or magnetic induction (I don't like this name since it has little to do with the effects of magnetic induction).
These Maxwell's equations tell the same story as those in vacuum but now we are dealing with free charges and free currents. The word free here means that these electric charges are not confined to one atom. They are not bound to a certian place of matter. If we are dealing with dielectrics or insulators then there are no free charges but if we are dealing with conductors then there certinally are some.
~ Waves in vacuum and matter ~
First of all let us untangle Maxwell's equations (figure 5) in vacuum. We will be using the following identity:
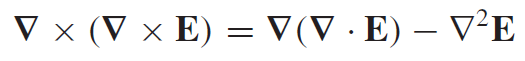
Eq10: Curl of Curl identity
If we apply the curl operator to the thrid Maxwell's equation we can use equation 10 for the left side, and on the right side we get the derivative of curl of the magnetic field "B". Now we can use the first (where rho is zero) and fourth (where "j" is zero) Maxwell's equation to neaten this up and what we get is something of a familiar form.
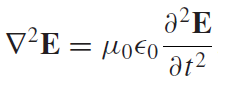
Eq11: Second order differential equation for E
What we see here is a classical wave equation (equation 1) but instead of it being in z-direction, this one is more general.
Same can be proven for the magnetic field "B" by applying the curl to the fourth Maxwell's equation and so on.
So Maxwell’s equations imply that empty space supports the propagation of electromagnetic waves, traveling at a speed:
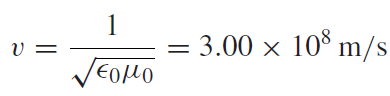
Eq12: Speed of electromagnetic waves in vacuum. Speed of light
We have now shown that Maxwell's equations allow wave-like solutions which means that the electric field "E" and magnetic field "B" can be written in the form of equation 4. It can also be shown that electromagnetic waves are transversal waves ("E" and "B" oscilate perpendicular to the direction of propagation). It can also be shown that "E" and "B" are always mutually perpendicular so if "E" is in x-direction then it follows that "B" is in the y-direction. Few more interesting results can be pulled out of Maxwell's equations but I don't want to go into too much detail. The amplitude of "B" can be rewriten in terms of amplitude of "E" and the speed of light which allows us to write "E" and "B" as:
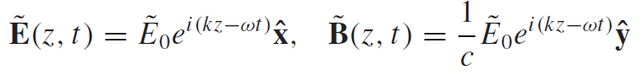
Eq13: Electric and magnetic component of electromagnetic waves in vacuum
So far we have been dealing with EM waves in vacuum. But what if we are in some kind of conductive matter. This means that free charge density and free current is not exactly zero. We can no longer unravel Maxwell's equations neatly because now equation 10 doesn't help us too much since divergence of "E" is no longer zero.
It can be shown that in so called Ohmic conducters (and most real conducters are ohmic conducters) this free charge density goes to zero if we let some time pass. All excess free charge accumulates on the surface leaving the interior free charge density = 0. This allows us to use equation 10 in a somewhat useful way. The free current density "J" does not usually go to zero so the only difference is made by the fourth Maxwell's equation.
Same as before - if we apply the curl operator to the forth Maxwell's equation and with the use of equation 10 we can arrive to classical wave equations, but now for conductors:
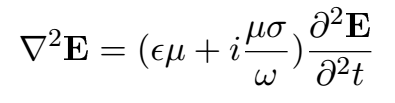
Eq14: Second order differential equation for E in conductors
Again, what we have now is a classical wave equation (equation 1) but instead of it being in z-direction, this one is more general. But there is now one mayor difference. Comparing this to equation 1 we can see that the speed of propagation is now a complex number! Since wave number "k" is related to the speed of propagation (angular frequency = wave number * speed of propagation) now even "k" is a complex number! The greek letter sigma symbolizes the electric conductivity.
Again "E" and "B" can be written as wave functions where now we have complex values:
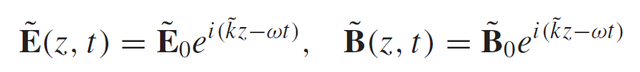
Eq15: Electric and magnetic component of electromagnetic waves in conductors
These equations will be used to show why mirrors reflect so much incident light and such a wide spectrum of colours unlike other materials.
The complex wave number "k" can be "pulled out" from complex speed and written as:
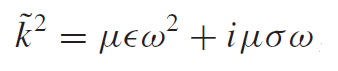
Eq16: Complex wave number
We can see that this complex wave number is related to the electric conductivity of matter and is proportional to it. Wave number "k" being a complex value causes waves to deteriorate inside conductors - they "die out". This will be very important for our case.
~ Fresnel equations ~
In the last section I tried to show how electromagnetic waves can be mathematically written when we observe them in conducting matter. Now we will look at what happens when some electromagnetic wave comes from vacuum or some insulator and hits a conducting surface. After all that is what is happening everyday around us. Light travels through air and for some reason reflects off some surfaces better and for some surfaces worse.
Let us observe the following situation:
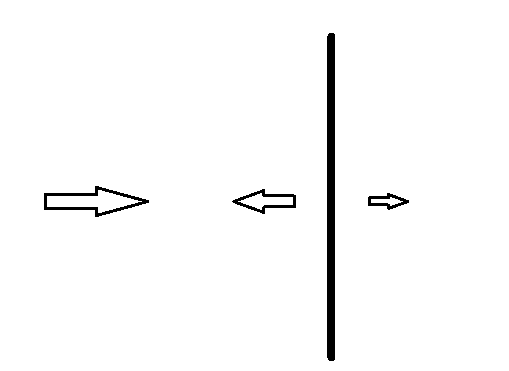
Fig7: Incident, reflected and transmitted wave
On the left we have a insulator and on the right we have a conductor. From the left arrives some incident electromagnetic wave and hits the surface head on. The incident wave (in insulator) can be written as:
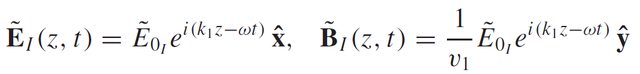
Eq17: Incident electromagnetic wave
Let's assume that a portion of this incident wave is reflected where it came from. So the reflected wave (still in insulator) can be written as:
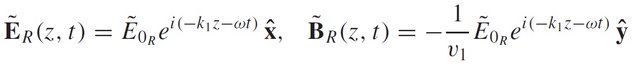
Eq18: Reflected electromagntic wave
And lastly let's assume that a portion of this incident wave managed to punch through and continue its propagation to the right. This transmitted wave (now in conducting matter) can be written with complex values:
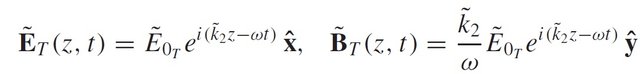
Eq19: Transmited electromagnetic wave
If we call everything happening on the left side "1" and everything happening on the right side "2" then at the border between these regions it must be true that:
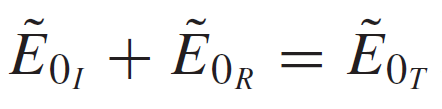
Eq20: Condition at the boundary
where index "0" implies we are talking about amplitudes. This must hold true and is almost intuitive since we can't expect a sudden jump in this amplitude when crossing the boundary.
Equation 19 (along with few sundries which arise from Maxwell's equation) gives us the following equations:
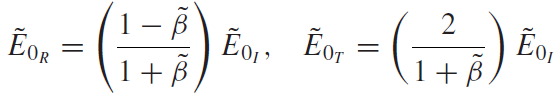
Eq21: Fresnel equations for perpendicular incidence
These equations tell us what part of the incident wave is reflected and what part of it is transmitted. We can see that the reflected and the transmitted part is written in terms of the incident wave and a new complex constant beta. This complex constant beta holds the key to our answer!
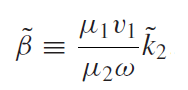
Eq22: Complex constant
This constant consists of all sorts of stuff. It contains constants of permeability (depents on the material), speeds of propagation and most importantly - the complex wave number. If we jump back to equation 16 we can see that this complex number is proportional with electric conductivity of matter.
What if we are dealing with perfect conducters? What would even be a perfect conducter? Well it would be some kind of matter which wouldn't resist to any electrical currents. It's electric conductivity would be infinite.
So let's see what happens if we take that electric conductivity (omega) goes to infinity. From equation 16 we see that "k" also goes to infinity. If "k" goes to infinity then according to equation 22, beta also goes to infinity. According to Fresnel equations (equation 21) we can see that if beta goes to infinity then the transmited amplitude goes to zero and reflected amplitude becomes same as the amplitude of the incident wave irregardless of its wavelenght or frequency!
We can now see that no matter what frequency / wavelenght of the incident wave actually is - everything will be reflected off of perfect conductors! That is why we see ourselves so clearly in mirrors.
In reality there are no perfect conductors but some materials come close to it. Silver for example is a great conductor which is why it is used for mirrors. In practice, you paint a thin coating of silver onto the back of a pane of glass (the glass has nothing to do with the reflection; it’s just there to support the silver and to keep it from tarnishing).
Silver is such a good conductor that the incident electromagnetic waves / light only penetrates is a few hundred atom lenghts. That is why we don't need a very thick layer.
I hope I managed to transfer some of my enthusiasm to you and that you find this as astonishing as I do :).
Cheers!
~ Short answer ~
We are all familiar with everyday concept of light. Everyday we observe that some things reflect light better than others. For example, my reflection in my smartphone screen is very dark and not very clear, but my reflection in mirror is basically a carbon copy of myself. What is it that mirrors posses and smartphone screens don't?
In the past it was not known exaclty what light actually is... It wasn't know if its speed is infinite or finite, and if it is finite than what speed does it travel at? All of these questions got their answer with the unification of the theory of electric fields and magnetic fields into electromagnetism and when it was shown that light is a electromagnetic wave.
Electromagnetism is almost completely "ruled" by Maxwell's equations - four differential equations which hold all secrets, tricks and phenomena of the electromagnetic world. From these equations it can be shown that electric and magnetic fields can be written in wave-like forms and many of their relations can be derived from the same equations.
Maxwell's equations really are powerful stuff!
With electric and magnetic fields written in terms of waves, one can mathematically begin to try to understand what happens when these waves pass through matter. Well electric and magnetic fields can act upon electric charges or currents by some force (electrostatic force and Lorentz force) and they can induce certian effects in matter which then alter the original electric and magnetic fields! These effects are called (electric) polarization and magnetization.
The same effects can be used to rewrite Maxwell's equations more compactly for cases when waves pass through matter - these equations are even more general than the original ones.
In case where this matter is conductive, these Maxwell's equations open up a whole new set of solutions. Electromagnetic waves in conductors have some new properties. A value called the wave number now becomes a complex value which causes the deterioration of electromagnetic waves in conductive matter. They become less and less powerful and eventually just "die out". This is very imporatnt for our topic of intrest beacause it can be shown that this wave number becomes bigger and bigger for better conductors.
Let's return to mirrors for a second... So what is happening? Light is arriving from outside and hits the mirror. This means that we must determine what happens on the point of "impact" where light "touches" the mirror.
When solving Maxwell's equations at this plane of contact, one can arrive to the so called Fresnel equations (equation 21) which tell us what part of the incident wave is reflected and what part is transmitted. It just so happens to be that for perfect conducters the transmitted part is zero and the reflected part is the same as the incident wave.
No matter what the colour or frequency of the incident light wave is all of it will be reflected if it hits a perfect conductor. Since silver is nearly a perfect conductor we don't need a very thick layer of it to make a mirror panel. What about the glass above the silver layer then? Well it is there just to keep it from tarnishing.
Thanks for checking this post out :)
Have a great day!
~ References ~
[1] - Griffiths, David J. (2012) - Introduction to Electrodynamics (4th ed.). Addison-Wesley.
[2] - Categories of waves
[3] - Fresnel equations
P.S. all equations were written by me in LaTeX / Texmaker!
Great post, keep up a good work :D
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sjajan i originalan post koji je privukao pažnju. Dobrodošao na Steemit! Verovatno je najbolje da se prijaviš na Discord i pronadješ SteemSTEM zajednicu i uputstva za pisanje. Možeš dobiti i mentora da te uvede u pravila. Osim na Engleskom, možeš pisati i na Hrvatskom. Sretna bronca u vaterpolu, čitamo se :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Puno hvala na lijepim riječima!
Svakako ću se prijaviti u Discord grupu i pogledati pravila, hvala na savjetu :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Imamo i naš lokalni jezički STEM tag (ne preterano aktivan, ali makar brojčano raste).
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Neka od pravila STEM-a:
Iz koje si oblasti fizike? :)
Javi mi se kad otvoriš Discord, zovem se isto i tamo
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @ulundo! You received a personal award!
You can view your badges on your Steem Board and compare to others on the Steem Ranking
Do not miss the last post from @steemitboard:
Vote for @Steemitboard as a witness to get one more award and increased upvotes!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit