Tal como los asombrosos cuerpos del universo con masas inmensas cuyos campos gravitatorios son tan intensos que ningún objeto, ni siguiera la luz, puede escapar de ellos, la sucesión de Collatz, llamada la Conjetura de Collatz, puede ser considerada un ¡agujero negro matemático!, pues cualquiera sea el número del cual se parta, conduce siempre al mismo resultado, es decir, ningún número puede escapar del "vórtice final" de la sucesión de Collatz.

Pero, ¿qué es la sucesión de Collatz?, ¿por qué es llamada conjetura?, ¿qué la convierte en un agujero negro matemático?, ¿existen otros agujeros negros matemáticos?
La Conjetura de Collatz
La conjetura de Collatz, también denominada la conjetura 3n+1, fue propuesta por el matemático alemán Lothar Collatz en 1937 [1]. Hasta el presente no ha sido demostrada ni refutada, ha sido verificada hasta con números muy grandes y tampoco se ha encontrado siquiera un contraejemplo que indique que es falsa (¡por eso es una conjetura!).
Respecto a la gran dificultad que ha representado encontrar una demostración de la conjetura de Collatz, el gran matemático húngaro del siglo pasado Paul Erdös, expresó lo siguiente:
"Las matemáticas no están listas para este tipo de problemas (...) Imposible, absolutamente imposible". [1]
Consiste en la sucesión cuyo primer término es cualquier entero positivo n y, los términos siguientes se obtienen dividiendo por dos el término anterior si éste es par, o multiplicándolo por tres y sumándole uno si es impar. Independientemente del valor de n, la secuencia siempre terminará en el número 1, de hecho en el ciclo 4, 2, 1. [2]
¡Asombroso!, ¿no?
En palabras del matemático estadounidense Jeffrey Lagarias, quien la ha estudiado intensamente:
"El problema 3n+1, también conocido como el problema de Collatz, el problema de Siracusa, el problema de Kakutani, el algoritmo de Hasse y el problema de Ulam, se refiere al comportamiento de los iterados de la función que para enteros impares n toma los valores 3n+1 y para enteros pares n toma valores n/2. La Conjetura 3n+1 afirma que, comenzando desde cualquier entero positivo n, la iteración repetida de esta función produce finalmente el valor 1.". [3]
Partiendo de la definición, la relación de recurrencia de la sucesión de Collatz es:
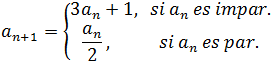
donde: 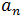 es cualquier término de la sucesión y
es cualquier término de la sucesión y 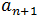 el término siguiente.
el término siguiente.
La fórmula general tiene la misma forma de la ecuación de recurrencia (¡otro dato curioso!), y para cualquier número entero n es:
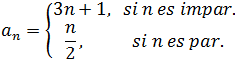

Algunos ejemplos de la Conjetura de Collatz
Con el primer término n = 2, al ser par, se divide entre dos obteniéndose 1. Considerando 1 impar, se multiplica por tres y se suma uno, obteniéndose 4, que al ser par se divide nuevamente por dos y se obtiene 2. Puede observarse que se entra al ciclo 4, 2, 1. Entonces, para n = 2, la sucesión de Collatz es: 2,1 (si se considera parar al obtener 1)ó 2, 1, 4, 2, 1, 4, 2, 1,…, considerando el ciclo 4, 2, 1 indefinido.
Con el primer término n = 3, siendo impar se multiplica por tres y se suma uno, obteniéndose 10, que al ser par se divide por dos y se obtiene 5, que es impar conduciendo a 16, que conduce a 8, a su vez 4, este a 2, y este a 1. Entonces, para n = 3, la sucesión de Collatz es: 3, 10, 5, 16, 8, 4, 2, 1.
Empezando en n = 4, al ser par, se divide entre dos obteniéndose 2, que a su vez conduce a 1. Entonces, para n = 4, la sucesión de Collatz es: 4, 2,1.
Para n = 5, la sucesión de Collatz obtenida es: 5, 16, 8, 4, 2, 1.
Empezando en n = 6, la sucesión de Collatz obtenida es: 6, 3, 10, 5, 16, 8, 4, 2, 1.
Comenzando en n = 34, la sucesión de Collatz es: 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.

Conclusiones
Si bien, la sucesión de Collatz tiene una relación de recurrencia simple, y cualquier persona que sepa suma, multiplicar y dividir puede construirla eligiendo el número inicial de su preferencia, hasta la fecha su demostración general ha sido esquiva a muchos de los grandes matemáticos del siglo XX y lo que va del XXI. Además, a pesar que se ha probado con muchos números, no se ha encontrado un contraejemplo que refute la conjetura.
Pero no deja de ser una mera curiosidad que ha atrapado a grandes matemáticos y al público general, sino que su demostración podría abrir las puertas de un cajón de nuevas y poderosas herramientas de varias ramas de las Matemáticas.
Para finalizar, ¿crees que existen otros agujeros negros matemáticos? Responderé a esta pregunta en un futuro post sobre el curioso mundo matemático.
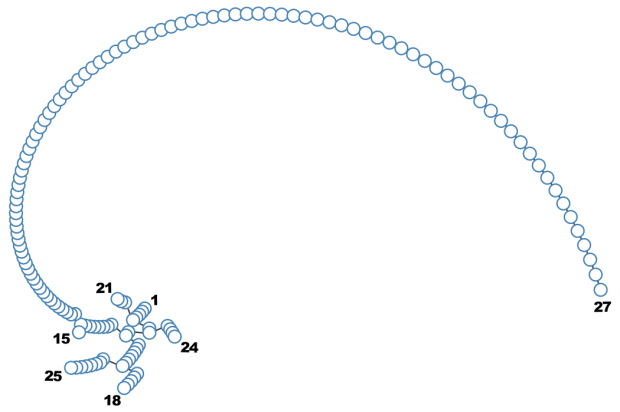
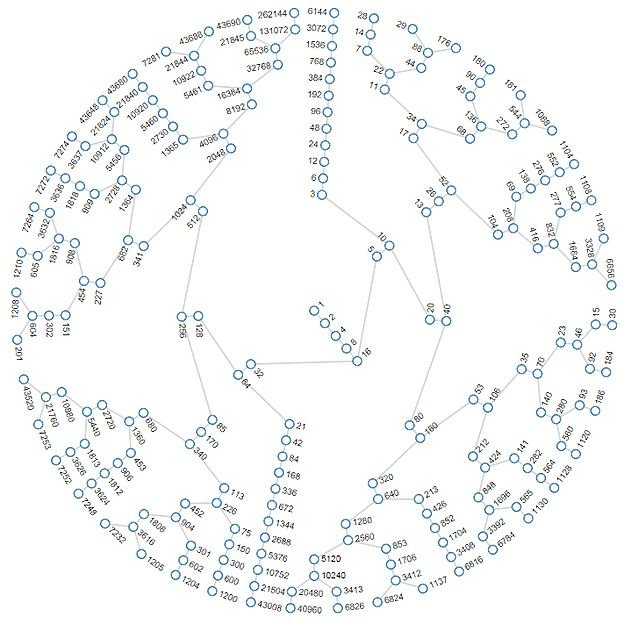
Por último, les presento otra excelente representación gráfica de varias sucesiones de Collatz, creada por el ingeniero de software Jason Davies, donde se observa como siempre llegan a 1.
Nota: Las ecuaciones fueron escritas en el editor de ecuaciones de Word.
Fuentes citadas:
[1] El más simple de todos los problemas matemáticos sin solución.
[2] Collatz conjecture – Wikipedia.
[3] The 3x+1 problem and its generalizations.
Fuentes consultadas:
[4] Fundación Polar, 2004. El Mundo de la Matemática. Fascículo 3. Sucesiones. Caracas: Últimas Noticias.
[5] Un agujero negro... y rojo.
[6] Mathemagical Black Holes.
[7] http://swimmingthestyx.com/p=447 - Graphing the Collatz Conjecture.
Espero que el post haya sido de tu interés y agrado. Si tienes cualquier pregunta o sugerencia, te invito a dejar tu comentario y con gusto te responderé. Gracias por tu amable lectura.
Muy buena tu publicación e interesante. Tienes una nueva seguidora y mi voto 😊
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @rossanavictora por tu comentario y tu voto. Me alegra que te haya gustado. También tienes un nuevo seguidor :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola amigo, excelente tema sobre la conjetura collatz, !! saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola amiga Edurley. Sí, además es un tema interesante: una de esas sorprendentes maravillas de las matemáticas que desconciertan y captan buestra atención. ¡Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy interesante tu artículo hermano. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hermano me alegra que te haya parecido interesante el post. Saludos y un abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy bueno tu articulo, saludos
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias Gary por tu comentario. Saludos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola amigo excelente trabajo el que has realizado para explicar esto!
Gracias por compartir!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola amiga Carla. ¡Gracias a ti por tu amable y motivador comentario!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
saludos @hugobohor excelente realmente tu artículo , nunca había visto esta sucesión , las matemáticas siempre sorprendiéndonos : -) te sigo
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @odic3o1. Comparto tu opinión acerca de las matemáticas, nunca dejan de sorprendernos. Me satisface que haya conocido la sucesión de Collatz a través del post. Gracias, te seguiré.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Me encanto super interesante, muy didáctica la forma de explicar dicha conjetura, a demás por un momento me traslade a las clases de señales donde, nos explicaban el comportamiento de las armónicas. Gracias por permitirme aprender un poco mas cada dia.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@anirdas me resulta motivador saber que el post te pareció interesante y que te haya gustado la forma en que presenté la conjetura. Gracias a ti por leerlo y disfrutarlo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
No conocía esa conjetura, muy buen post.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola Estefany. Me agrada saber que conociste esta fascinante y desconcertante conjetura hasta ahora imposible. ¡Saludos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Amigo y perijanero hermano @hugobohor. De verdad, me gustó mucho este post. Felicitaciones!.
Un caluroso abrazo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hermano perijanero @tsoldovieri, me alegra mucho que te haya gustado el post. Gracias por las felicitaciones. ¡Un abrazo fraterno!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Crees que podrá tener alguna aplicación tecnológica?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Hola Emily. Desconozco si tiene alguna aplicación tecnólogica. Como dato curioso ha sido usada para estudiar la también "desconceertante" sucesión de los números primos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Excelente post! Tienes mi voto.
Tengo una pregunta: Cómo se dibuja la sucesión en el plano XY? Por ejemplo, en un dibujo partes de 27 y dicha sucesión tiene como 50 números hasta llegar al uno, pero la sucesión se dibujó formando una curva, ¿esta curva es arbitraria? o tiene algún sentido.
Un saludo.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias @jga. La gráfica de una sucesión en el plano cartesiano, al ser una función, se contruyen de la misma manera, salvo que sólo se marcan los puntos correspondientes a los pares ordenados (n, f(n)), aunque algunos autores también trazan rectas entre los puntos.
Ahora bien, si se quieren trazar las gráficas de varias sucesiones de Collatz a la vez, se han encontrado muchas formas, pero en el caso de las gráficas mostradas en el post en forma de "agujeros" se analizan previamente las secuencias y se tratan de dibujar en una misma curva aquellas que tengan elementos comunes. En cierta forma los radios de curvatura de las curvas si son arbitrarios. Te recomiendo para que profundices en la explicación que te di, la referencia [7].
Espero haberte ayudado con la respuesta. Gracias por la visita.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit