Saludos mis estimados amigos de la comunidad científica #stem-espanol
¿Qué voy a presentar en este artículo?
Pues continúo el estudio de la cola de Urbach en el espectro de absorción óptica, debido a que la variación de la energía de Urbach con la temperatura no se ajusta bien con los modelos propuestos en la literatura.
Esto nos llevó a la formulación de una ecuación que se ajustara a los puntos experimentales y que tuviera una explicación física aceptable!
Para tratar de ajustar los datos experimentales de la EU en silicio amorfo hidrogenado (SiH0.13), Cody et al. [a] introdujeron un término independiente de la temperatura en la ecuación (1):

donde el parámetro X lo relaciona con el desorden estructural presente en los materiales amorfos o con defectos.
Cuando utilizamos esta ecuación (1) a nuestros resultados de EU con la temperatura en varias muestras de CuInTe2 y CuGaTe2, no se ajustó a los puntos experimentales!. A pesar de esto, se determinó que el incremento de hνp se relaciona con el desorden estructural X, por lo que se propone la ecuación (2) que expresa tal dependencia:
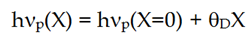
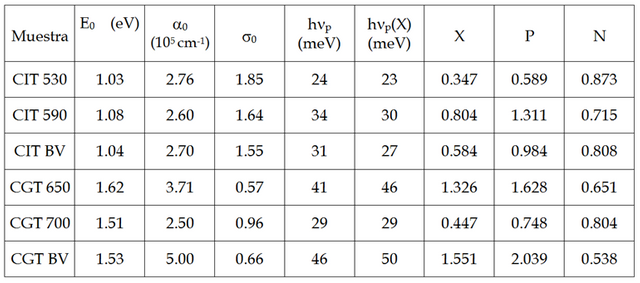
Usando el valor reportado de θD = 172 K y hνp(X=0) = 17 meV, obtenido del ajuste lineal en la figura 1, se calcula hνp(X) con la ecuación (2). Estos valores se indican en la tabla 1 y concuerdan con los obtenidos del ajuste de σ vs T, que se indicaron en la publicación anterior. Aquí, sigo insistiendo que por cualquier lado que analicemos los fenómenos físicos, deberíamos obtener los mismos resultados y de esta manera se verifica la validez de la ecuación (2) propuesta.
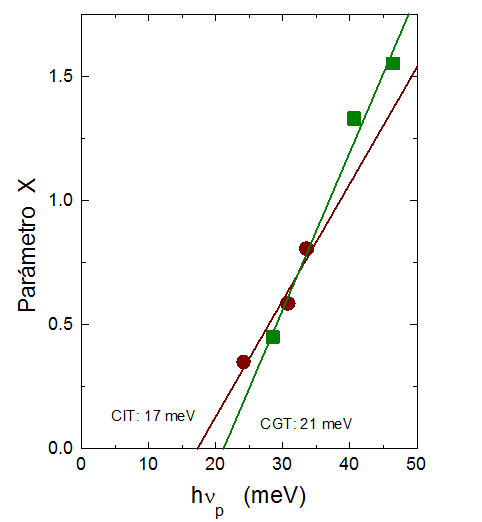
Figura 1. Variación del parámetro de desorden estructural X con la energía del fonón asociada con la cola de Urbach, en las muestras de CuInTe2 y CuGaTe2.
Se observa que el parámetro X aumenta de una muestra a otra a medida que se incrementa hνp. Esto confirma que el alto valor de la energía del fonón está relacionado con el desorden estructural, tal como lo propone Cody.
A pesar de esto, la ecuación (2) no reproduce satisfactoriamente la dependencia de EU con la temperatura, pues el ajuste a los datos experimentales no es muy preciso, como se presentó en la figura 6 de la publicación anterior.
Para explicar esta discrepancia entre los datos experimentales y el ajuste teórico, se ha propuesto una versión modificada de la ecuación (2) que incluye un parámetro adicional en el término térmico dado por (Kθ/σ0)(eθ/T - 1)-1. Esto se explica debido a que se espera que la desviación de la estequiometría ideal de lugar a un desorden estructural y a una relación de compensación que varíe de una muestra a otra y probablemente causa modificaciones en la distribución de los fonones, por lo que sólo hay una contribución parcial de los fonones a la expresión térmica. De esta manera, la nueva formulación para el análisis de la energía de Urbach está dada por la ecuación (3):
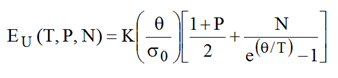
donde P y N están relacionados con el desorden estructural y la modificación del término de los fonones térmicos, respectivamente. En un sistema perfectamente ordenado se espera que P = 0 y N = 1.
En la figura 2 se observa la dependencia de la energía de Urbach con la temperatura y el ajuste de los datos con la ecuación (3), con P y N como parámetros variables. Los valores de estos parámetros se indican en la tabla 1. En esa tabla se observa que sólo una fracción del total de modos de los fonones interactúan con electrones/excitones, ya que el parámetro N varía entre 0 y 1.
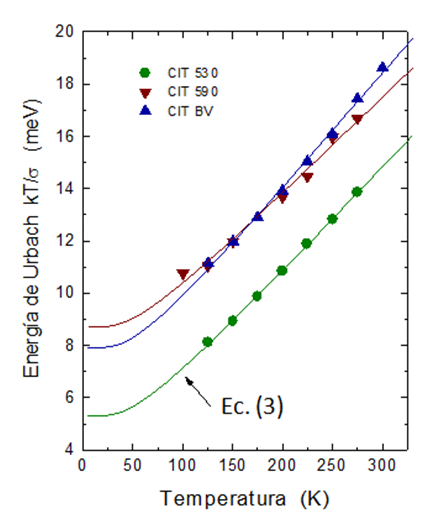
Figura 2. La energía de Urbach en función de la temperatura en tres muestras de CIT.
Explicación de los términos introducidos en la nueva ecuación de la energía de Urbach
La variación de P y N con hνp en las muestras de CIT se presenta en la figura 3. Se observa que P se incrementa linealmente con hνp, por lo que la extrapolación lineal hasta P = 0 da un valor de hνp = 17 meV. Este valor concuerda con la energía promedio de los fonones ópticos reportados y señalados en el texto y sugiere que la energía del fonón en P = 0 o X = 0 efectivamente corresponde a dicho promedio de energía.
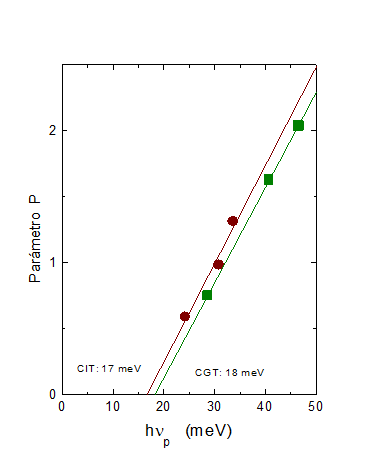
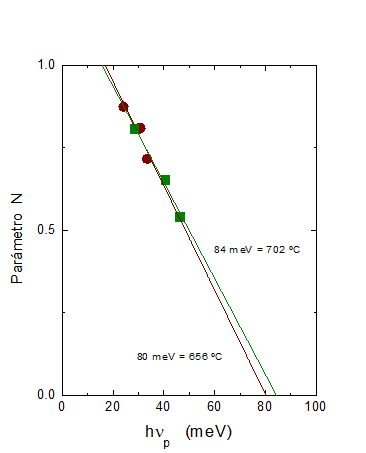
Figura 3. Variación de los parámetros relacionados con el desorden estructural P y la modificación del término térmico N (Ec. 3). En un sistema perfectamente ordenado se esperaría que P = 0 y N = 1. Se incluyen los datos experimentales del semiconductor CuGaTe2 para poner a prueba la nueva ecuación propuesta por nuestro grupo de trabajo.
Como se sabe, estos materiales experimentan una transición de fase en el estado sólido desde la fase ordenada calcopirita a la desordenada esfalerita a la temperatura de 670 ºC (CIT) y 795 ºC (CGT), que corresponden a 81 meV y 92 meV, respectivamente. En el caso de CIT concuerda con la energía de 84 meV obtenido en N = 0. Esto implica que en el máximo desorden representado por N = 0 se espera que ocurra una transición de fase relacionado con el orden-desorden estructural.
Tabla 1. Los parámetros E0, α0, σ0 y la energía del fonón hνp asociada a la cola de Urbach, el parámetro de desorden estructural X de la Ec. (2) y las variables P y N de la Ec. (3), en las muestras de CIT y CGT.
En conclusión:
- Se ha establecido la presencia de la cola de Urbach justo por debajo de la brecha de energía en el espectro de absorción a diferentes temperaturas, tanto en CIT como en CGT.
- Se encontró una relación lineal entre el término de desorden estructural X o P con la energía del fonón hνp en la interacción electrón/excitón. La extrapolación de esta relación hasta X=0 o P=0 concuerda con la energía promedio de todos los modos ópticos reportados en estos materiales.
- La versión modificada (Ec. 3) de la relación empírica de Cody et al. (Ec. 1), que toma en cuenta el efecto del desorden estructural sobre el término térmico, ajusta muy bien los datos experimentales de la variación de la energía de Urbach con la temperatura.
- Según el análisis realizado anteriormente, el estudio de la cola de Urbach en varias muestras semiconductoras que tengan diferente magnitud del desorden estructural podría utilizarse como un método alternativo para obtener una buena estimación de la temperatura de Debye (Ec. 2) y puede aportar una información relacionada con la transición de fase estructural en la extrapolación de N vs hνp hasta N = 0.
¿Qué les pareció este tipo de caracterización óptica de materiales semiconductores?
Para un científico no basta con realizar las mediciones rutinarias y aplicar los modelos existentes, siempre existirá un aporte a la ciencia, ya sea innovando o proponiendo una nueva formulación para explicar nuestro "mundo científico".
En la próxima publicación les presentaré más temas relacionados con las propiedades ópticas de los materiales, porque es una línea de investigación muy extensa y amplia para seguir desarrollando investigación científica!
Referencias:
[a] CODY G.D., TIEDJE T., ABELES B., BROOKS B., GOLDSTEIN Y. Phys Rev Lett 47: 1480-1483, 1981.
Lectura recomendada:
ABAY B., GÜDER H.S., EFEUGLU H., YOGURTÇU Y.K. Turk J Phys 25: 543-549, 2001.
URBACH F. Phys. Rev. 92: 1324-1325, 1953.
WASIM S.M., BONALDE I., MEDINA E., MARÍN G., RINCÓN C. J Phys Chem Solids 66: 1187-1191, 2005.
HOLAH G.D., SCHENK A.A., PERKOWITZ S., and TOMLINSON R.D. Phys. Rev. B 23, 6288 – 6292, 1981
ABAY B., GÜDER H.S., EFEUGLU H., YOGURTÇU Y.K. J Appl Phys 84: 3872-3879, 1998.
Esas relaciones son fenomenológicas o surgen de alguna teoría?
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Existe una teoría muy amplia y bien fundamentada en la formulación de esta nueva ecuación. Por desgracia ya existen pocos grupos de investigación que se dedican a estudiar este fenómeno en diferentes materiales semiconductores, lo cual reforzaría la explicación física que tienen los nuevos parámetros introducidos!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @iamphysical. Interesante artículo!.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias amigo @tsoldovieri
La idea es que los usuarios se interesen en las diferentes técnicas de caracterización de materiales!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muy interesante tu post amigo, lo encontré por casualidad pero ahora me quedo siguiéndote! me gustaría invitarte a que pases por mi blog pero para que te unas a mi comunidad, sé que a mis amigos también les gustarían mucho tus publicaciones, y viendo que tienes experiencia me gustaría invitarte a ser uno de los administradores.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Muchas gracias por tu propuesta. Siempre estoy a la orden para colaborar en beneficio de la comunidad steemit.com
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @iamphysical. Me llamo mucho la atención lo que escribes al final de post: "Para un científico no basta con realizar las mediciones rutinarias y aplicar los modelos existentes, siempre existirá un aporte a la ciencia, ya sea innovando o proponiendo una nueva formulación para explicar nuestro "mundo científico". Muchas veces, se usan las mediciones de forma rutinaria, pero no se buscan alternativas innovadoras que permitan salir de lo convencional. Muchos éxitos.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Con esta publicación ya cumplí mi misión, que es despertar esa curiosidad científica de mis estimados investigadores en dar un paso más en la búsqueda de cosas nuevas!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit