Propiedades ópticas de los semiconductores: variación de la brecha de energía con la temperatura

Saludos mis estimados usuarios de la comunidad científica #stem-espanol

Esta vez les presento un tema de interés a la hora de caracterizar los materiales semiconductores, la variación de la brecha de energía al disminuir la temperatura desde 300 K hasta 10 K usando un criostato de helio. Con este experimento podemos obtener valores nominales de ciertos parámetros físicos como: temperatura característica de Einstein, temperatura de Debye, coeficiente de variación de la brecha de energía con la temperatura, además de analizar la contribución de: excitones, dilatación térmica e interacción electrón-fonón como causantes de dicha variación.

Ya sabemos cómo determinar el valor de la brecha de energía E_G para transiciones directas entre la banda de valencia y la banda de conducción en el semiconductor CuInTe₂ por el método de extrapolación, ahora veremos detalles del método de Elliot [a] que es una adaptación estadística de la teoría propuesta por Hennerberger [b] sobre las transiciones ópticas.

Equipo y rango de medición

En la figura 1 observamos el equipo utilizado para estudiar la variación de la brecha de energía con la temperatura entre 10 K y 300 K, se utiliza un criostato de ciclo cerrado marca Acton SpectraPro 2750 (SP-2750) enfriado con helio gaseoso.

Figura 1. Criostato o “dedo frío” y partes del espectrofotómetro: monocromador, cámara portamuestra de medidas ópticas (CPMO), cabezal del criostato (CC), sistema mecánico-eléctrico (SME) y lámpara de xenón (LX).

Aquí debemos revisar los detectores del haz de fotones de la radiación incidente, ya que al bajar la temperatura hasta 10 K el valor de E_G aumenta y disponemos de los siguientes detectores: InGaAs ID-441 que tiene un rango de 850 a 1700 nm (0,73 a 1,46 eV) y Si-440-UV-P en un rango de 200 a 1050 nm (1,18 a 6,20 eV). Como el CuInTe₂ tiene una E_G = 0,98 eV utilizamos el detector ID-441.

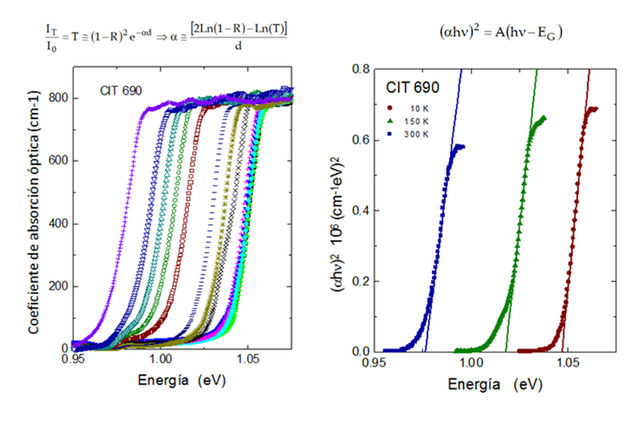
Vamos a aplicar lo que vimos en la publicación anterior y calculamos el coeficiente de absorción óptica para cada temperatura desde 10 K hasta 300 K, como se ve en la figura 2.
Se determina la brecha de energía por el método de extrapolación, como se ve en la figura 3.

.

Variación de la brecha de energía al bajar la temperatura

Para explicar el comportamiento de la brecha de energía en función de la temperatura (E_G vs. T), se utiliza el modelo empírico propuesto por Manoogian-Woolley [c] que incluye separadamente el efecto de la dilatación térmica de la red y la interacción electrón-fonón. En esta aproximación, la variación de E_G con la temperatura está dada por:

donde U, S y V son parámetros independientes de la temperatura y θ es la temperatura característica de Einstein y está vinculada con la temperatura de Debye por la relación θ ≈ ¾ θ_D

Se grafica la dependencia de E_G con la temperatura, figura 4. La línea continua es el ajuste que se hace con el modelo empírico propuesto por Manoogian-Woolley [c]

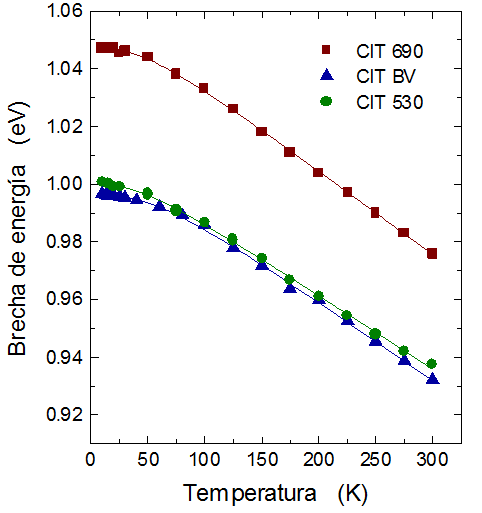
Figura 4. Dependencia de la brecha de energía obtenida por el método de extrapolación con la variación de la temperatura. Los parámetros de ajuste se indican en la tabla 1.

En los compuestos ternarios de cobre se ha determinado que el 80% de la variación de la brecha de energía con la temperatura se debe principalmente a la contribución de la interacción electrón-fonón y el 20% a la contribución de la dilatación térmica de la red. Un caso curioso ha sido en CuInSe₂ que ha mostrado un comportamiento anómalo a bajas temperaturas.

Hasta aquí no debería haber ningún problema, pues los diferentes gráficos vienen de cálculos ya explicados y el ajuste a los puntos experimentales vienen de los modelos empíricos propuestos en la literatura.

Sin embargo, viene el famoso "pero", los valores obtenidos por el método de extrapolación no son muy precisos. Esto se debe a la contribución de excitones al coeficiente α cerca del borde de absorción fundamental. En algunos casos estos no son observados como picos en las curvas α vs. hν, debido a que su energía de enlace es muy pequeña. Para determinar un valor más confiable de E_G, las curvas de α en el rango de temperatura desde 10 K hasta 300 K son analizadas usando el modelo propuesto por Elliot [a]. Este incluye los términos de contribución discreta y continua del excitón.

El coeficiente de absorción es expresada mediante la ecuación:

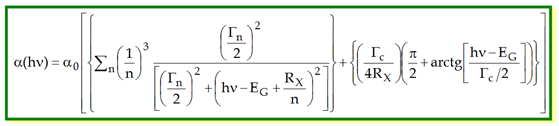
donde α₀ representa el pico de absorción del excitón en el estado base con energía de enlace R_X, Γ_n/2 y Γ_c/2 son los anchos de línea a media altura de la Lorentziana y del continuo del excitón, respectivamente.

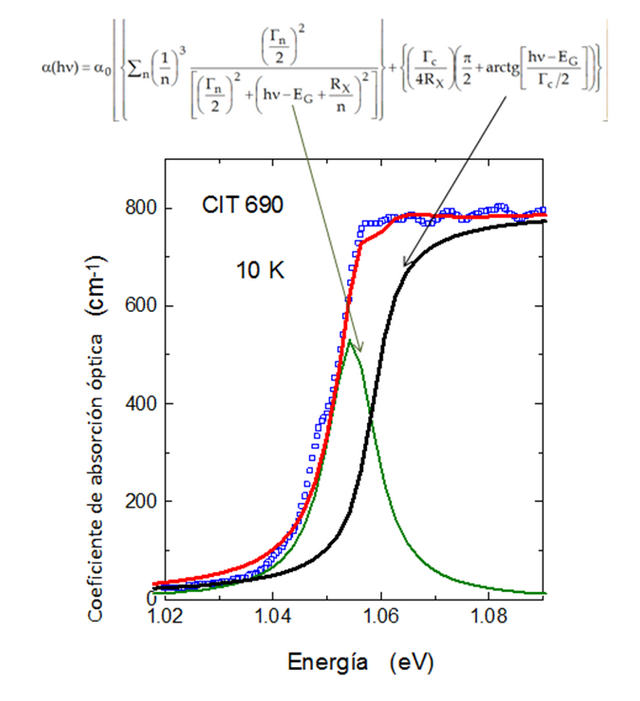
Figura 5. Se indican el ajuste realizado con el modelo de Elliot (rojo) y las contribuciones del excitón libre (verde) y del continuo (negro) a 10 K en CuInTe₂.

Este proceso lo hacemos para cada temperatura y obtenemos los parámetros de ajustes importantes para mi (en particular) como el valor de la brecha de energía que toma en cuenta la contribución de los excitones, que con el método de extrapolación se ignoraban, y la energía de enlace del excitón que me servirá para calcular la masa efectiva de huecos y electrones en este material semiconductor.

Ya vieron ¿porqué es importante aplicar los modelos físicos para caracterizar los materiales? y todo este procedimiento porque estamos estudiando la estructura de bandas en los materiales semiconductores, como les mencioné en la publicación anterior!

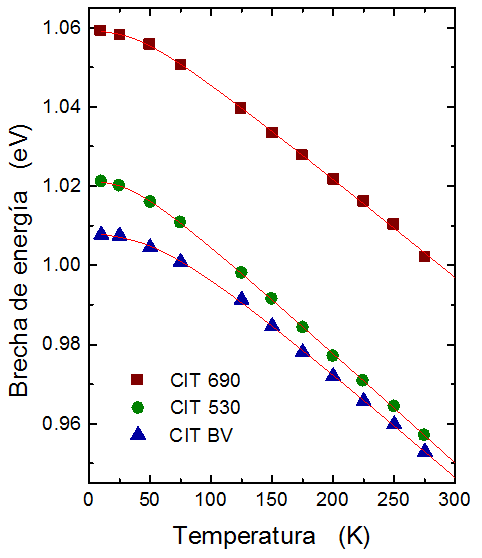
Figura 6. Dependencia de la brecha de energía obtenida por el método de Elliot con la variación de la temperatura. Los parámetros de ajuste se indican en la tabla 1.

Tabla 1. Valores de los parámetros E_G(0), U, V y θ_D obtenidos del ajuste con la ecuación Manoogian-Woolley de las curvas E_G vs T por: extrapolación "a" y modelo de Elliot "b", respectivamente.

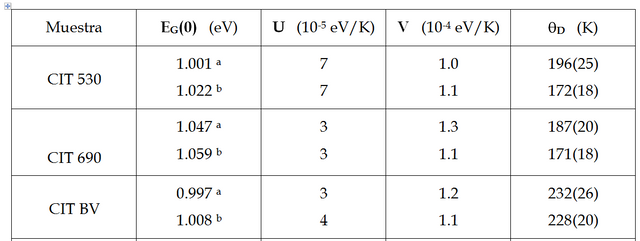
Vamos a hacer un análisis de estos resultados experimentales, ¿que les parece?

Comparando los resultados de E_G obtenidos por los dos métodos se observa que para la muestra CIT 690 a 10 K, por extrapolación se obtiene E_G = 1,047 eV, mientras que el calculado con el modelo de Elliot E_G = 1,059 eV. Este valor es mayor debido a que considera la contribución de excitones en los procesos de absorción óptica y la diferencia es de aproximadamente 10 meV, que es en promedio la energía de enlace del excitón libre!
Eso es bueno, las cuentas cuadran perfectamente!

Los valores de θ_D obtenidos están de acuerdo con lo reportado para θ_D = 165 K y 191.4 K [d].

La variación de la E_G con la temperatura en el rango de 10 K y 300 K es de aproximadamente 100 meV, esto también se ha observado en otros materiales semiconductores de la familia Cu-III-VI₂.

Pero, no crean que esto llega hasta aquí!

No, continúa y con los mismos resultados vamos a hacer otros análisis!

¿Qué tal si para la próxima publicación seguimos estudiando la estructura de bandas de este semiconductor y analizamos la "cola de Urbach"?

Por aquí les menciono algunas referencias casi que obligatorias cuando se hace la caracterización óptica y las que utilicé en esta publicación.

Jacques I. Pankove. Optical Processes in Semiconductors, Dover Publications (1971), 422 p.
K.V. Shalímova. Física de los semiconductores. Editorial Mir, (1975), 319 p.
R.B. Adler, A.C. Smith, R.L. Longini. Introducción a la Física de los semiconductores, SEEC, tomo 1, Editorial Reverté S.A. (1970), 239 p.
J. L. Shay and J. H. Wernick, Ternary Chalcopyrite Semiconductors:Growth, Electronic Properties and Applications, Pergamon, New York, 1974.
[a] R. J. Elliot, Phys. Rev. (1957) 108, 1384.
[b] F. Henneberger. phys. stat. sol. (b) (1986) 137, 371.
[c] A. Manoogian and J. C. Woolley, Can. J. Phys. (1984) 62, 285.
[d] V. Riede, H. Neumann, H. Sobotta, R. D. Tomlinson, E. Elliott, and L. Howarth, Solid State Commun. (1980) 23, 557 .