El potencial hídrico (Ψw) puede ser una medida útil para determinar el estado hídrico de las plantas. En estas se ve influenciado mayormente por tres factores: la concentración de solutos (potencial osmótico, Ψπ), la presión electroestática (potencial de presión) y la gravedad (potencial de gravedad) los cuales determinan el Ψw de los distintos tejidos y este a su vez influencia el movimiento del agua en la planta. En el presente estudio, se describe la determinación del potencial hídrico de tubérculos de Solanum tuberosum y Daucus carota y de hojas de Phaseolus vulgaris mediante gravimetría en función de los cambios al ser sometidas a una batería de soluciones con concentraciones de sacarosa diferentes y mediante la bomba de Scholander respectivamente. De manera similar, se calcula el Ψw y Ψπ de hojas y raíces de P. vulgaris empleando el método densitométrico de Chardakov. Finalmente, se midió la tasa de transpiración de Codiaeum sp. bajo diferentes condiciones de demanda evaporativa. Entre algunas conclusiones, se obtuvo que el Ψw de las hojas y raíces de P. vulgaris fue de -0,19 ± 0,02 y -0,14 ± 0,02 MPa respectivamente.
1. INTRODUCCIÓN
El agua es el componente químico más abundante en las plantas, llegando a alcanzar hasta entre un 80 y 95% del peso neto de los tejidos activos. Sus propiedades fisicoquímicas (molécula de tamaño pequeño y de naturaleza dipolar; alta polaridad y capacidad de formación de puentes de hidrógeno; altos valores de calor específico y de vaporización; facilidad para disolver sales iónicas; alta adhesión, cohesión y tensión superficial que permiten la capilaridad y la alta fuerza tensil) explican que esta pueda cumplir gran variedad de funciones en la planta (Barceló et al., 2014; Campbell et al., 2014). Así, el agua es el principal constituyente del citoplasma, es disolvente de gases, iones y nutrientes que difunden por toda la planta, y participa en procesos metabólicos y en el mantenimiento de la turgencia y de la temperatura mediante la transpiración (Barceló et al., 2014). El movimiento del agua en la planta, desde el suelo hasta las hojas y luego la atmósfera (el denominado continuo suelo-planta-atmósfera), está regido por gradientes de potencial hídrico (Ψw), de mayor potencial a menor potencial. En sí, Ψw es una medida del potencial químico del agua, es decir de la cantidad de energía libre asociada a esta, dividido entre el volumen molal parcial del agua, y usualmente expresado en mega Pascales (MPa) (Taiz & Zeiger, 2002).
En las plantas, los tres factores que influencian mayoritariamente al Ψw son la concentración de solutos, la presión y la gravedad. El primero se conoce como potencial de soluto o potencial osmótico (Ψπ) y representa el efecto de solutos disueltos sobre el Ψw. El segundo, la presión hidrostática o potencial de presión (Ψp), puede ser positivo si se trata de la presión de turgor o negativo si se trata de tensión. Por su parte, el tercer factor, la gravedad (Ψg), causa que naturalmente el agua tienda a moverse hacia abajo. Dicho esto, el Ψw se puede expresar en función de estos tres factores como: Ψw = Ψπ + Ψp + Ψg , en donde Ψg es solo considerado por encima de 10 m de altura y Ψπ=-RTCs según la ecuación de van’t Hoff (Azcón-Bieto & Talón, 2008; Taiz & Zeiger, 2002).
Normalmente la determinación del Ψw se basa en que cuando una célula o tejido esta en equilibrio con el líquido o vapor que lo rodea, el flujo dinámico es cero, es decir Ψw célula = Ψw medio , por lo que el Ψw de la solución patrón o medio nos suministra el valor de Ψw de la célula o tejido. En función de esto, la determinación puede darse al sumergir una muestra o tejido en distintas soluciones patrón de Ψw conocido y por observación de las variaciones de peso o volumen se puede saber el Ψw del tejido, que corresponde al de la solución en donde no tenga ningún cambio apreciable de peso (método gravimétrico) (Barceló et al., 2014).
Otros procedimientos, como el método de Chardakov, utilizan cambios densitométricos en las soluciones patrón en las que previamente se había introducido la muestra o tejido para reconocer el equilibrio y por tanto el Ψw (Barceló et al., 2014). Algunos, se basan en el equilibrio de vapor en vez de líquido, usando psicrómetros de termopar. De los métodos más empleados, por su rapidez y practicidad, se encuentra el método de la cámara de presión diseñado por Scholander, en el que el Ψw de las células de las hojas se compensa externamente por una presión ejercida en la cámara hasta que sobresale sabia del xilema. Este valor de presión externa, es aproximado al Ψw del tejido foliar (Barceló et al., 2014; Taiz & Zeiger, 2002).
El interés de estudio del estado hídrico y las relaciones hídricas radica en que son de importancia central en la economía y optimización del agua para la planta y en los mecanismos internos reguladores frente a la situación hídrica exterior (Barceló et al., 2014). En función de lo antes expuesto, en el presente estudio se describe la determinación del potencial hídrico de tubérculos de Solanum tuberosum y Daucus carota mediante el método gravimétrico, y del potencial hídrico y osmótico de hojas y raíces de Phaseolus vulgaris mediante el método densitométrico de Chardakov y la cámara de presión de Scholander. Finalmente, se describe también la determinación de la tasa de transpiración de Codiaeum sp en diferentes condiciones de iluminación (demanda evaporativa).
2. MATERIALES Y MÉTODOS
2.1. Determinación del potencial hídrico de tubérculos de Solanum tuberosum y Daucus carota mediante gravimetría
Empleando un horadador, se prepararon cilindros de dos tubérculos de papa (S. tuberosum) y de una zanahoria (Daucus carota) de 2 cm de longitud. En el caso de la zanahoria, estos se realizaron tanto en la zona del xilema, como en la corteza y se trabajaron por separado. Cada cilindro se pesó y se colocó en 20 mL de una única solución de sacarosa, haciendo lo mismo con varios cilindros y con una batería de soluciones de concentración 0, 0.1, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50 y 0.60 M. Luego de una hora, se retiraron los cilindros de la solución y se secaron ligeramente, determinando en este momento su peso final. Mediante una regresión lineal, potencial de la solución vs. diferencial de peso se calculó el Ψw de los tejidos.
2.2. Determinación del potencial hídrico y osmótico en hojas y raíces de Phaseolus vulgaris por el método densitométrico de Chardakov
Con la ayuda de un abre huecos, se hicieron discos de hojas de plántulas de caraota (P. vulgaris ). Se colocaron 25 discos de hojas sin nervaduras en tubos conteniendo 5 mL de una solución de sacarosa a una concentración específica dejándolo así durante una hora. La soluciones empleadas fueron de 0, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08, 0.1, 0.2 y 0.5 M. En el caso de las raíces, se pesaron 0,9 g de raíz para cada solución y se dejaron igualmente una hora. Terminado el tiempo de incubación, se agregaron dos gotas de azul de metileno al 1 % en cada tubo. Empleando una pipeta, se colocó una gota sumergida de la solución coloreada a aproximadamente 1 cm de la superficie en otra solución de la misma concentración. Se observó si la gota subía o bajaba. Para la determinación del potencial osmótico, se realizó exactamente el mismo procedimiento antes descrito, con la salvedad de que los discos de hojas fueron congelados a 4 °C durante 15 min, y luego introducidos en las respectivas soluciones.
2.3. Determinación del potencial hídrico en hojas de Phaseolus vulgaris regadas y en déficit hídrico empleando la cámara de presión de Scholander
Se usaron plántulas de caraota (P. vulgaris ) a las que se les realizó un corte limpio y rápido en el tallo. Inmediatamente después de ser cortada la plántula fue puesta en el tapón de la cámara de Scholander (Scholander et al., 1956) asegurándose que el extremo cortado sobresaliese de esta. Empleando la válvula de presión y la lupa, se aplicó aire comprimido a la cámara lentamente hasta que se observó que el tejido alrededor del corte se impregnó de nuevo en agua. En este punto de registro la presión marcada en el manómetro. Para esto se usaron tres plántulas en déficit hídrico y tres en buenas condiciones y se procesaron individualmente. Se evaluó diferencias empleando el software PAST 3.1, y la prueba de ANOVA (α=0,05).
2.4. Determinación de la tasa de transpiración de Codiaeum sp. bajo diferentes condiciones de iluminación
Tabla I. Promedio de diferenciales de masa de cilindros de S. tuberosum en el primer y segundo ensayo. Se observa ganancia de masa entre 0,20 y 0,25 M para el primer ensayo y entre 0,25 y 0,30 M en el segundo, representado por el cambio de signo.
| Sacarosa (M) | Ψw solución (MPa) | Diferencial de masa ensayo 1 (g) | Diferencial de masa ensayo 2 (g) |
|---|---|---|---|
| 0 | 0,0000 | 0,0333 | 0,05555 |
| 0,1 | -0,2478 | 0,0201 | 0,0355 |
| 0,15 | -0,3717 | 0,0143 | 0,0275 |
| 0,20 | -0,4956 | 0,0126 | 0,0150 |
| 0,25 | -0,6195 | -0,0127 | 0,0020 |
| 0,3 | -0,7434 | -0,0432 | -0,0295 |
| 0,35 | -0,8673 | -0,0756 | -0,0755 |
| 0,4 | -0,9912 | -0,0951 | -0,0930 |
| 0,45 | -1,1151 | -0,0985 | -0,1240 |
| 0,5 | -1,2390 | -0,1278 | -0,1480 |
| 0,6 | -1,4868 | -0,1535 | -0,1765 |
Tres tallos cortados de Codiaeum sp. o planta del croto fueron cortados bajo el agua y colocados en cilindros graduados obteniendo un volumen final de 10 mL. Una de ellas, recibió iluminación directa alta (flujo fotónico 35 w/m2), la otra una iluminación mediana producida por el mismo flujo fotónico pero con un filtro de agua, y la tercera con iluminación ambiental normal. Cada 15 min se determinó el volumen de la disminución de agua en el cilindro, la temperatura ambiental, la foliar y la humedad relativa del aire. Finalizado el ensayo, se midió el área foliar dibujando el contorno de las hojas en papel milimetrado y luego pesándolo y calculando la relación masa- área tomando como referencia el peso de 1 cm2. La tasa de transpiración se calculó como masa de agua perdida (mg)/ área foliar (cm2) y se expresó en un gráfica en función del tiempo. Las tasas de transpiración se compararon con la prueba de Kruskall-Wallis (α=0,05) y los de temperatura mediante ANOVA.
3. RESULTADOS
3.1. Determinación del potencial hídrico en tubérculos de S. tuberosum y D. carota mediante gravimetría
Para los tubérculos de S. tuberosum se observó que entre 0,20 y 0,25 M en el primer ensayo (Tabla I) y entre 0,25 y 0,30 M en el segundo ensayo hubo una ganancia de peso en los cilindros, representada por el cambio de signo en los diferenciales, de positivo a negativo. Se detalla además, que a pesar de lo antes mencionado, los diferenciales no fueron en ningún momento iguales a cero, sino que oscilaron alrededor de este en un rango o intervalo en específico. Por su parte, tanto en la corteza de D. carota como en el xilema (Tabla II) se detalló una ganancia de masa en los cilindros, representada nuevamente por el cambio de signo en el diferencial, entre 0,40 y 0,45 M. Ningún valor diferencial fue exactamente cero, a pesar de que algunos si se acercaron. Al realizar la regresión para los ensayos con S. tuberosum se observó que los datos se ajustaron al modelo lineal con valores de coeficiente de determinación (R2) de 0,9535 en el primer ensayo y 0,9592 en el segundo. Similarmente, la regresión para los datos de D. carota en la corteza y el xilema fueron arrojó valores de R2 de 0,9606 y 0,3932.
Tabla II. Promedio de diferenciales de masa de cilindros de D. carota tanto en la corteza como en el xilema. Se observa una ganancia de masa entre 0,40 y 0,45 M, representada por el cambio de signo en los diferenciales, de positivo a negativo.
| Sacarosa (M) | Ψw solución (MPa) | Diferencial de masa promedio corteza (g) | Diferencial de masa promedio xilema (g) |
|---|---|---|---|
| 0 | 0,0000 | 0,0745 | 0,0084 |
| 0,1 | -0,2478 | 0,0613 | 0,0272 |
| 0,15 | -0,3717 | 0,0572 | 0,0281 |
| 0,20 | -0,4956 | 0,0459 | 0,0269 |
| 0,25 | -0,6195 | 0,0409 | 0,0298 |
| 0,3 | -0,7434 | 0,0297 | 0,0124 |
| 0,35 | -0,8673 | 0,0176 | 0,0138 |
| 0,4 | -0,9912 | 0,0080 | 0,0287 |
| 0,45 | -1,1151 | -0,0121 | -0,0484 |
| 0,5 | -1,2390 | -0,0193 | -0,0043 |
| 0,6 | -1,4868 | -0,0577 | -0,0294 |
Con los ajustes realizados, se calcularon los valores de Ψw de todos los tejidos (Tabla III) observándose que tanto el valor promedio de Ψw en S. tuberosum como en el valor calculado en el xilema de D. carota se salen del intervalo de potencial antes establecido en función de los cambios de signo en los diferenciales de masa. Además, se observa que el Ψw calculado para el xilema es menor que el de la corteza.
Tabla III. Rango de potencial hídrico (Ψw) y Ψw calculado mediante la regresión para tubérculos de D. carota y S. tuberosum. Se puede observar que algunos valores se salen del intervalo establecido en el ensayo gravimétrico.
| Planta | Rango Ψw según el ensayo (MPa) | Ψw calculado (MPa) |
|---|---|---|
| S. tuberosum (tubérculos) | -0,49 a -0,74 | -0,44 ± 0,05 |
| D. carota (corteza) | -0,99 a -1,12 | -1 |
| D. carota (xilema) | -0,99 a -1,12 | -0,98 |
3.2. Determinación del potencial hídrico y osmótico en hojas y raíces de P. vulgaris por el método de Chardakov
En el ensayo para determinar Ψπ se pudo ver que la gota coloreada descendía en todos los casos, hasta que en 0,5 M ascendió (Tabla IV). De manera similar, se observó que la gota ascendió en 0,08 M y 0,06 M para hojas y raíces respectivamente. En función de esto se calcularon los valores promedio para los potenciales (Tabla V), pudiéndose detallar que el Ψw en las hojas es menor que en raíces y que ambos son mayores que el Ψπ de las hojas.
Tabla IV. Dirección de la gota coloreada en los ensayos de Chardakov para calcular el potencial hídrico (Ψw) de la hoja y la raíz, y osmótico (Ψπ) en la hoja. En todos los casos la gota desciende (-) y en algún punto empieza a ascender (+).
| Sacarosa (M) | Ψw de la solución | Ψπ hoja | Ψw hoja | Ψw raíz |
|---|---|---|---|---|
| 0 | 0,0000 | - | - | - |
| 0,03 | -0,0743 | - | - | - |
| 0,04 | -0,0991 | - | - | - |
| 0,05 | -0,1239 | - | - | - |
| 0,06 | -0,1486 | - | - | + |
| 0,07 | -0,1734 | - | - | + |
| 0,08 | -0,1982 | - | + | + |
| 0,1 | -0,2478 | - | + | + |
| 0,2 | -0,4956 | - | + | + |
| 0,5 | -1,2390 | + | + | + |
Tabla V. Potenciales hídricos (Ψw) de la hoja y la raíz y osmótico de la hoja (Ψπ) de P. vulgaris calculados mediante el método de Chardakov.
| Ψπ hoja (MPa) | Ψw hoja (MPa) | Ψw raíz (MPa) |
|---|---|---|
| -0,86 ± 0,53 | -0,19 ± 0,02 | -0,14 ± 0,02 |
Fue posible además calcular el potencial de presión de la hoja (Ψp) en función del Ψw y Ψπ. Este tuvo un valor de Ψp= 0,67 MPa, demostrando que las células del tejido se encontraban turgentes.
3.3. Determinación del potencial hídrico en hojas de P. vulgaris regadas y en déficit hídrico empleando la cámara de presión de Scholander
Se pudo determinar que el valor de Ψw promedio para las hojas en plantas hidratadas fue de -0,52 ± 0,03 y de -0,77 ± 0,13 para las deshidratadas. Mediante la prueba de ANOVA se determinó la existencia de diferencias (p=0,02), presentando las plantas en déficit hídrico un valor menor de Ψw que en las plantas bien hidratadas.
3.4. Determinación de la tasa de transpiración de Codiaeum sp. bajo diferentes condiciones de iluminación
En la Figura 1, se pueden observar las tasas de transpiración de Codiaeum sp. bajo iluminación nula, con filtro y directa. En la planta con filtro, la tasa de transpiración fue aumentando uniformemente en comparación con las otras dos plantas en diferentes condiciones. Además, alcanzó la tasa de transpiración más alta entre todas, en aproximadamente 6 mg/cm2. En contraste, la planta con iluminación nula, fue aumentando más lentamente su tasa de transpiración, alcanzando a penas un máximo de aproximadamente 3 mg/cm2. Por su parte, la planta que recibió iluminación directa alcanzó rápidamente una elevada tasa de transpiración, seguida de un largo periodo en el que esta se mantuvo relativamente constante. Luego de lo cual empezó a aumentar su actividad discretamente, llegando hasta una tasa máxima de aproximadamente 4,5 mg/cm2.
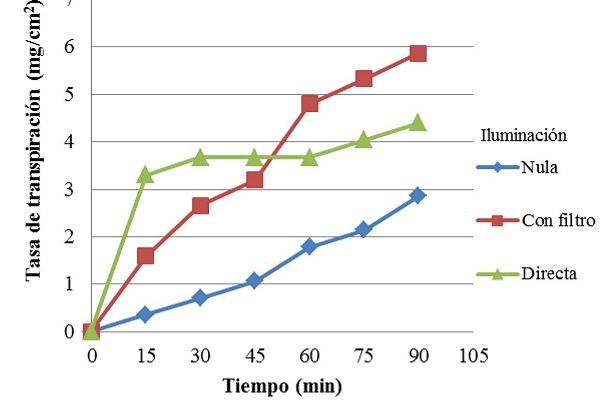
Figura 1. Tasa de transpiración de Codiaeum sp. bajo diferentes condiciones de demanda evaporativa. La planta que recibió iluminación a través de un filtro, presentó la máxima tasa de transpiración, mientras que la mínima la alcanzó la planta con iluminación nula. Por su parte, la planta con iluminación directa presentó un periodo en el cual su tasa de transpiración se mantuvo contante.
De manera similar, se observó que con iluminación nula, la temperatura foliar promedio fue casi idéntica a la ambiental (Tabla VI), mientras que el iluminación directa y con filtro, la foliar tendió a ser menor que la ambiental. Por su parte, la prueba de Kruskal-Wallis demostró que existían diferencias (p<0,05) en cuanto a las tasas de transpiración de la planta con iluminación nula y directa, mientras que la tasa de transpiración de la planta con iluminación indirecta no fue diferente a las demás (Mann-Whitney). Por otro lado, los valores de temperaturas no fueron diferentes entre si (p>0,05).
Tabla VI. Temperatura foliar y ambiental promedio, y humedad relativa promedio en las tres condiciones de iluminación. Humedad relativa promedio del aire: 71% ± 5,1
| Iluminación | Temp. Foliar promedio (°C) | Temp. Ambiental promedio (°C) |
|---|---|---|
| Nula | 28,2 ± 0,3 | 28,1 ± 0,05 |
| Con filtro | 31,1 ± 1,9 | 31,6 ± 1,6 |
| Directa | 40,5 ± 6,1 | 40 ± 5,4 |
4. DISCUSIÓN
4.1. Determinación del potencial hídrico en tubérculos de S. tuberosum y D. carota mediante gravimetría
En el ensayo gravimétrico, se observaron cambios en los diferenciales de peso en función de si los cilindros de tejido ganaban o perdían masa de agua. Este movimiento de agua, se debe principalmente al gradiente de Ψw entre el medio y el interior de las células. En este sentido, si el tejido ganó agua, significa que el Ψw del tejido es menor que el del medio, y si perdió agua, significa que el Ψw del tejido era mayor al de la solución (Barceló et al., 2014). Cuando no se observa variación, quiere decir que el potencial del tejido y el medio, es el mismo.
En los ensayos realizados, se observó que algunos de los valores de Ψw calculados se encontraron por fuera del intervalo experimental (Tabla III). Esto es debido a que los valores calculados se basan en una predicción establecida mediante un modelo matemático lineal, al cual los datos no se ajustaron del todo bien, posiblemente debido a desviaciones experimentales. En todo caso, el Ψw calculado para S. tuberosum se puede comparar con el determinado en otros estudios mediante cámaras de presión, correspondiendo a plantas bien hidratadas (Liu et al., 2005).
Por su parte, el potencial hídrico determinado para el xilema y la corteza de D. carota implican que el agua que pasa a través de tubérculo se direcciona hacia la corteza en vez de al xilema para subir hasta las hojas, ya que el Ψw es menor en la corteza. De entrada, esto es contrario a lo esperado, ya que el agua que entra por la raíz se dirige al xilema y de allí a las hojas, conformando el conocido continuo suelo planta atmósfera (Taiz & Zeiger, 2002). Esto, aunado al hecho de que el ajuste de los datos al modelo lineal fue bastante bajo, invita a pensar que los resultados están fuertemente influenciados por errores durante la experimentación. Por lo que sería prudente repetir el ensayo en condiciones más controladas.
4.2. Determinación del potencial hídrico y osmótico en hojas y raíces de P. vulgaris por el método de Chardakov
En el método de Chardakov, el fenómeno de que la gota ascienda o descienda en una solución que se supone era de su misma concentración, es una forma indirecta de estimar si las densidades de ambas soluciones son iguales. Así, si el tejido absorbió agua porque su Ψw es menor al del medio, este tiende a estar ahora más concentrado, es decir, más denso y por tanto a descender en una solución de menor densidad. Al contrario, si el tejido aportó agua al medio, este se diluye y disminuye su densidad, lo que determina que ascienda en un medio más denso. En función de esto, la concentración o rango en el que la gota cambia de ascender a descender o viceversa, representa el rango de concentración en el que el potencial del tejido es igual al del medio (Barceló et al., 2014).
Con base en esto, fue posible determinar que el Ψw en la raíz es mayor al de las hojas de P. vulgaris (Tabla V), lo cual es coherente con lo esperado si se entiende que para que el agua ascienda desde el suelo, pasando por la raíz, el xilema y finalmente hasta las hojas, se requiere de un gradiente de Ψw. En el que las hojas, por ser el órgano en donde se da la transpiración poseen un potencial menor al del resto de la planta ya que en ellas se evapora el agua y por tanto el Ψπ es siempre bajo (Taiz & Zeiger, 2002; Konrad & Wilhelm-Wolfgang, 1982). Esto último se corresponde también con lo encontrado, ya que el Ψπ en la hojas fue bastante menor con relación al Ψw , lo que implica que la célula se encontraba turgente, y existía un Ψp tal que el Ψw no fuese tan bajo como el Ψπ. Dicha presión de turgencia, permite inferir que el tejido se encontraba bien hidratado.
4.3. Determinación del potencial hídrico en hojas de P. vulgaris regadas y en déficit hídrico empleando la cámara de presión de Scholander
La determinación del Ψw en un tejido en específico mediante la cámara de Scholander se basa en que al romper la tensión de la columna de agua en el xilema, el agua es atraída hasta las hojas en función del gradiente de Ψw (si se trata de un tejido que transpira, ya que de no serlo no existiría gradiente de Ψw y el agua se dispersaría a los alrededores del xilema por ósmosis y no hacia las hojas) hasta que el gradiente no existe y el Ψw del xilema y las hojas son el mismo. Una vez en este punto, se agrega presión externa que logra desplazar el agua fuertemente atraída a las hojas hacia el xilema hasta su estado inicial. De manera que la presión ejercida es aproximadamente el valor de Ψw de las hojas, asumiendo que el Ψπ en el xilema es muy bajo (Taiz & Zeiger, 2002). En los ensayos realizados en P. vulgaris mediante este método, se pudo determinar que el Ψw de hojas de plantas hidratadas es mayor al de las hojas de plantas en déficit hídrico. Lo cual se explica porque al no haber suficiente agua en el suelo, existe un breve periodo antes de que la transpiración cese, en el que el agua que pierde la hoja no es suplida, de manera que los solutos se concentran y aumentan el Ψπ y por tanto el Ψw, ayudado además por la desaparición de la presión de turgencia (Trejo & Davies, 1991).
4.4. Determinación de la tasa de transpiración de Codiaeum sp. bajo diferentes condiciones de iluminación
Si bien solo se encontraron diferencias en cuanto a la tasa de transpiración entre la planta con iluminación nula y directa, se comparan todas en función de su tendencia y de lo que ocurre en la planta. En especial dado el hecho de que si se realizaran varias medidas y se compararan punto a punto, muy probablemente se encontraran diferencias entre las tres plantas en la mayoría del tiempo. Las temperaturas también se evalúan en función de tendencia. Para empezar, se observa que la planta con mayor tasa de transpiración fue la planta con iluminación indirecta. Esto es debido a que al tener un filtro de agua, la luz aún llegaba a las hojas pero la energía térmica asociada a esta era filtrada o absorbida y disipada por el agua. De manera que se observó un aumento casi lineal de la tasa de transpiración respecto al tiempo.
Contrariamente, la planta con iluminación directa al no poseer ningún filtro recibió toda la luz y energía térmica, lo cual aumentó su temperatura hasta por encima de los 40 °C, valor en el que las hojas de la zona superior murieron, deteniendo súbitamente la tasa de transpiración, que luego empezó a aumentar muy discretamente. Probablemente debido a que algunas de las hojas de la zona inferior de la planta, al encontrarse más lejos de la fuente de luz aun transpiraban aunque a tasas muy bajas. Finalmente, la planta con iluminación nula solo se valió de la luz ambiental residual para transpirar. De manera que su tasa de transpiración fue siempre más baja en los otros dos casos, y aumentó muy lentamente.
5. CONCLUSIONES
• El potencial hídrico calculado mediante gravimetría para tubérculos de S. tuberosum fue de -0.44 ± 0,05 MPa.
• El potencial hídrico del xilema y corteza calculado mediante el método gravimétrico en D. carota son respectivamente -0,98 y -1.00 MPa.
• Los potenciales hídricos de la hoja y raíz de P. vulgaris calculados a partir de método densitométrico de Chardakov son -0,19 ± 0,02 y -0,14 ± 0,02 MPa respectivamente. Por su parte el potencial osmótico calculado para las hojas fue de -0,86 ± 0,53 MPa.
• El potencial de presión de las hojas de P. vulgaris calculado fue de 0,67 MPa.
• Mediante el método de la cámara de presión de Scholander se determinó que el potencial hídrico de plantas hidratadas es estadísticamente mayor que el de plantas con déficit hídrico. Presentado valores de -0,52 ± 0,03 y -0,77 ± 0,13 MPa.
• La tasa de transpiración máxima fue alcanzada por la planta de Codiaeum sp. sometida a iluminación con un filtro de agua. Presentando un aumento aproximadamente lineal.
• La tasa de transpiración mínima la presentó la planta de Codiaeum sp. con iluminación mínima o nula. Siendo esta diferente de la tasa de la planta con iluminación directa.
• En la planta de Codiaeum sp. sometida a iluminación directa se observó la muerte de algunas hojas y el detenimiento temporal del aumento de la tasa de transpiración.
6. REFERENCIAS BIBLIOGRÁFÍCAS
Azcón-Bieto, J. & M. Talón. (2008). Fundamentos de fisiología vegetal. McGraw Hill Interamericana. Madrid, España.
Barceló, J., G. Nicolás, B. Sabater & R. Sánchez. (2014). Fisiología Vegetal. Ediciones Pirámide. Madrid, España.
Campbell, N., J. Reece, L. Urry, M. Cain, S. Wasserman, P. Minorsky & R. Jackson. (2014). Biology. Pearson Education, Inc. Estados Unidos de América.
Konrad, K. & A. Wilhelm-Wolfgang. (1982). Effect of potassium on the water potential, the pressure potential, the osmotic potential and cell elongation in leaves of Phaseolus vulgaris. Physiol. Plant. 54: 402-408.
Liu, F., C. Jensen, A. Shahanzari, M. Anderson & S. Jacobsen. (2005).ABA regulated stomatal control and photosynthetic water use efficiency of potato (Solanum tuberosum L.) during progressive soil drying. Plant Science.168: 831-836.
Scholander, P., F. Hammel, H. Bradstreet & D. Hemtningsen. (1965). Sap pressure in vascular plants. Science. 148: 339-346.
Taiz, L. & E. Zeiger. (2002). Plant physiology. Sinauer Associates, Inc. Sunderland, Estados Unidos de America.
Trejo, C. & W. Davies. (1991). Drought-induced Closure of Phaseolus vulgaris L Stomata Precedes Leaf Water Deficit and any Increase in Xylem ABA Concentration. Jour. Exper. Bota. 42(245): 1507-1515.
Wow es mucha información la que compartes aqui y muy interesante, supongo que esta información la usa mucho mi tio ya que maneja varios invernaderos de jitomates
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos, intento mostrar los trabajos con el mayor detalle que puedo para llevar al lector paso a paso a través de mis investigaciones en biología experimental
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
muy buena info, muy interesante gracias por tu aporte :D!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Gracias a ti, intentaré seguir subiendo información interesante
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Saludos @khrisaeroth, interesante ensayo realizaste con tres cultivos de interés agroalimentario , los aspectos fisiológicos que abordaste en tu post son de importancia para conocer el comportamiento de algunos cultivos, permitiendo tomar decisiones al momento de establecerlos. saludos !
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
This post has been voted on by the steemstem curation team and voting trail.
There is more to SteemSTEM than just writing posts, check here for some more tips on being a community member. You can also join our discord here to get to know the rest of the community!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you so much!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Congratulations @khrisaeroth! You have completed the following achievement on Steemit and have been rewarded with new badge(s) :
Click on the badge to view your Board of Honor.
If you no longer want to receive notifications, reply to this comment with the word
STOPDo not miss the last post from @steemitboard:
SteemitBoard World Cup Contest - Semi Finals - Day 1
Participate in the SteemitBoard World Cup Contest!
Collect World Cup badges and win free SBD
Support the Gold Sponsors of the contest: @good-karma and @lukestokes
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
¡Felicidades, #proconocimiento te valoró!
Has sido reconocido(a) por tu buen post por el Comité de Arbitraje y Valoración del Proyecto Conocimiento @proconocimiento.
Apoyamos y valoramos tu esfuerzo...
Proyecto Conocimiento es parte de la comunidad @provenezuela.
Pioneros en la plataforma #steemit en el reconocimiento y valoración a la Producción Intelectual en habla hispana.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit