En primer lugar mis saludos respetuosos para toda la comunidad de #stem-espanol, #steemstem, #utopian-io y #proconocimiento, así como para el resto de la prestigiosa comunidad de steemit, continuando con la temática geometría y su importancia en nuestro desempeño tanto en lo académico como en lo profesional. En esta oportunidad les estaré hablando sobre la Geometría analítica la cual representa desde su llegada la aplicación del lenguaje algebraico así como el análisis matemático a la geometría en general, lo cual impactó positivamente en todo el campo de las matemáticas, la ciencia y otras áreas de desarrollo humano, iniciaremos con el estudio de los aspectos fundamentales de la geometría analítica plana en una primera entrega, ya que la misma constituye la base para la comprensión de esta fabulosa parte de las matemáticas como lo es la geometría analítica.

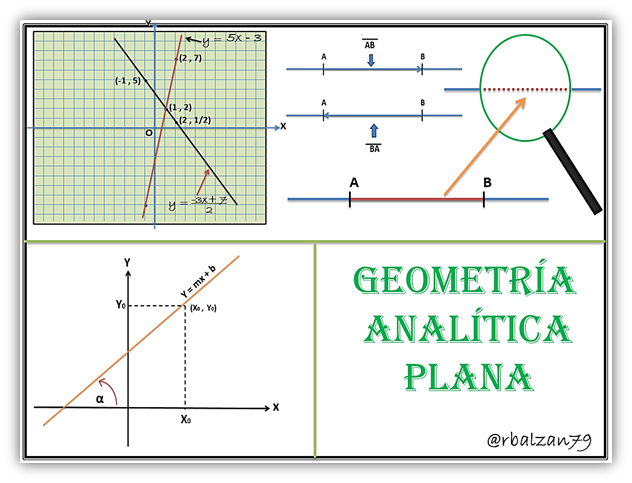
Podemos decir que la geometría analítica plana tiene como principio fundamental asociar cada punto ubicado en el plano con un único par ordenado de números, pero que análogamente a cada uno de estos pares ordenados de números le corresponda únicamente un punto en el plano, pero antes de seguir profundizando en este aspecto conoceremos algunos conceptos y propiedades fundamentales que nos permitan ir construyendo tal principio fundamental de la geometría analítica plana, tan importante para el aspecto analítico en cualquier aspecto matemático, por lo tanto, estaremos estudiando puntos conceptuales tales como:

• Segmento rectilíneo.

• Segmento rectilíneo dirigido.

• Sistema coordenado lineal o unidimensional.

• Distancia entre dos puntos dados.

• Sistema coordenado bidimensional o plano cartesiano.

• Funciones afines o lineales, la recta en el plano.

• Método gráfico para solucionar un sistema lineal de dos ecuaciones y dos incógnitas (2x2).

En la pasada publicación pudimos conocer algunas propiedades e importantes conceptos que caracterizan y fundamentan a la geometría elemental, también conocimos debido al amplio alcance de estudio de la geometría las ramificaciones de las mismas, en donde encontramos a la geometría analítica plana, la cual será objeto de estudio en esta publicación, esto en una primera entrega de este capítulo de dicha geometría analítica plana, aquí les dejo el enlace de mi publicación anterior Importancia de la geometría.

Para construir el aprendizaje de cualquier tipo de conocimiento siempre es importante dar a conocer los aspectos conceptuales, es decir, aquellos que soportan o fundamentan toda la estructura de dicho conocimiento, por lo tanto, ese será nuestro propósito inicial dar a conocer algunos de estos conceptos fundamentales para la geometría analítica plana, así pues, podremos notar cómo es posible generalizar muchos de los principios o nociones de la geometría elemental mediante la aplicación de métodos utilizados por la geometría analítica, en este preciso momento al introducirnos al estudio de la geometría analítica plana, es necesario resaltar que el docente pueda enlazar algunos conocimientos previos de sus estudiantes en cuanto a la conceptualización de geometría elemental (punto, recta, plano, trigonometría, por nombrar algunos) con nuevos aspectos o métodos analíticos de carácter geométricos.

Unos de los principales propósitos de esta publicación es poder dar a conocer algunos conceptos básicos para la geometría analítica plana, con la finalidad de ir conformando las bases fundamentales para el entendimiento de esta parte de la geometría analítica, en su aspecto o carácter bidimensional, por lo tanto, tenemos:

Segmento rectilíneo:

Para conceptualizar este término es importante tener presente lo siguiente, desde el punto de vista de la geometría elemental conocemos que todo conjunto de punto forma lo que nosotros conocemos como figuras, en donde encontramos desde la línea recta hasta cualquier figura geométrica conformada por un determinado conjunto de puntos, ahora bien, un segmento es considerado como una porción o parte de una línea recta, donde el mismo está determinado o limitado por dos puntos perteneciente a dicha recta a los que denominamos extremos del segmento, entonces, en términos más precisos, podemos decir que, un segmento representa un subconjunto de puntos de una recta, ejemplo:

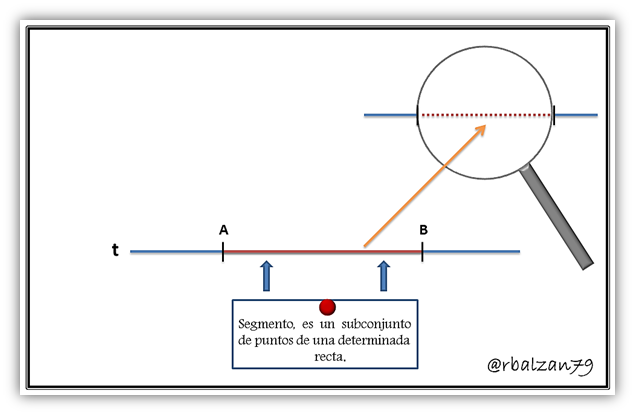
Segmento rectilíneo dirigido:

Es muy probable que estén familiarizados con el concepto antes descrito en la geometría elemental, pero ahora debemos inyectarle algunas propiedades utilizadas por la geometría analítica a la anterior definición de segmento con el firme propósito de estructurar nuevos fundamentos y poderlos utilizar en la conformación de conceptos más complejo, entonces, añadiremos a la anterior definición de segmento rectilíneo o simplemente segmento la idea de sentido o dirección (orientación), desde este punto de vista le damos al segmento (ahora segmento rectilíneo dirigido) una capacidad de movimiento de uno de sus puntos, este punto ira o seguirá el sentido o dirección de la punta de una fecha, la cual representara tal sentido o dirección , por ejemplo:

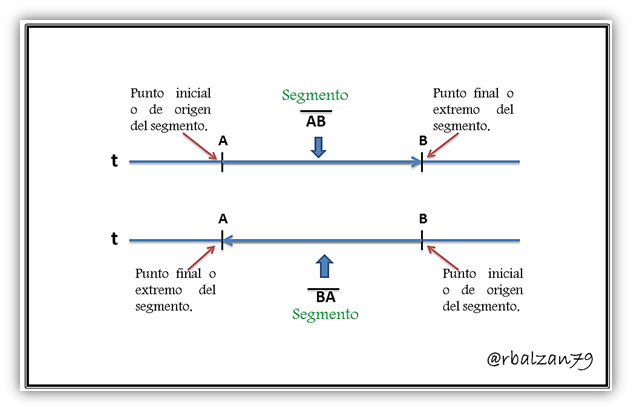
Por lo tanto, podemos decir que el segmento AB es originado por un punto el cual se moviliza por toda la recta (t) con el sentido o la dirección de A hacia B, donde el punto A representara nuestro origen y B nuestro extremo, pero en termino analítico es posible también obtener el mismo segmento con el sentido o dirección contraria, es decir, de B hacia A en donde nuestro punto de origen seria ahora B y nuestro extremo A, entonces, el sentido o dirección de un determinado segmento dirigido lo indicamos siempre colocando primero el punto de origen o inicial.

Entonces, desde el punto de vista analítico ya le hemos dado sentido o dirección a un segmento que ahora lo denominamos segmento dirigido, sin embargo, seguiremos inyectándole propiedades analítica ahora al segmento dirigido, para la geometría elemental las longitudes de los segmentos dirigido para nuestro caso los segmentos AB y BA son iguales, desde el punto de vista de la geometría analítica podemos hacer una distinción en cuanto a sus longitudes mediante la utilización de signos, las mismas serán positivas (+) o negativas (-), por lo tanto, podemos especificar de manera arbitraria (aspecto que nos permite otorgar características adecuadas para un determinado análisis) que un determinado segmento dirigido en un sentido lo consideremos de longitud positiva, en donde el otro, dirigido en sentido opuesto lo consideremos un segmento de longitud negativa, ejemplo:

En nuestros segmentos dirigidos anteriores, es decir, AB y BA podemos asignarle una longitud positiva al segmento dirigido con sentido de A hacia B, por lo tanto, el segmento dirigido de B hacia A tendrá una longitud negativa, ejemplo:

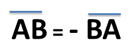
Otro ejemplo: Considerando que la longitud positiva del segmento dirigido es la que tiene dirección en el sentido de la punta de la flecha, es decir, de izquierda a derecha, tenemos entonces la siguiente relación de longitudes:

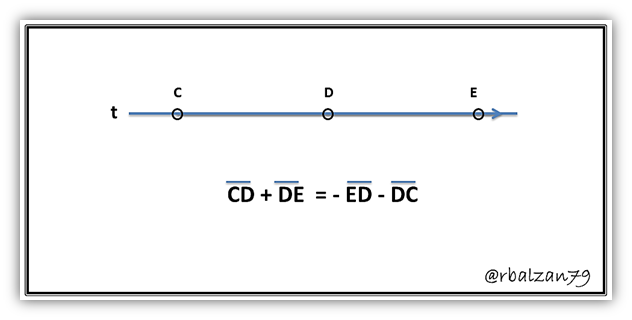
Sistema coordenado lineal:

Hasta ahora hemos ido concatenando y dando características analítica al concepto de segmento llevándolo a un segmento dirigido (orientado, con sentido o dirección) y después otorgándole un signo a su longitud de acuerdo al sentido que arbitrariamente queramos que sea positiva o negativa dicha longitud, todo dependerá del análisis que deseemos realizar, ahora daremos otro paso más en cuanto a la fundamentación de la geometría analítica plana, en donde introduciremos la idea de proporcionalidad entre un punto geométrico y un determinado número, con la finalidad de poder dar sentido o conformación a un sistema coordenado lineal, el cual nos llevará a dar los pasos necesarios para la conformación de los demás sistemas coordenado tanto en el aspecto bidimensional o tridimensional.

Inicialmente identificamos nuestra recta X´X la cual será la base de nuestro sistema coordenado lineal, podemos determinar su dirección positiva de izquierda a derecha, en donde dicha recta posee un punto fijo al cual denominaremos (O) el mismo será nuestro punto referencial o de origen, es importante que consideremos una distancia conveniente (proporcional) la cual nos servirá como unidad de medida para nuestro sistema coordenado lineal, si tenemos que (B) es un punto de dicha recta pero distinto de (O) y a su vez situado a su derecha, la longitud (OB) podemos considerarla como nuestra unidad de longitud (carácter de proporcionalidad), ya que el segmento esta entre 0 y 1, pero consideremos otros puntos tales como (R) el cual puede ser un punto cualesquiera de dicha recta base y situado también a la derecha de (O), entonces dicho segmento dirigido (OR) cuya longitud es positiva contiene longitud (x) veces a la unidad establecida proporcionalmente, por lo que podemos decir que dicho punto (R) corresponde al número positivo (x), de igual manera podemos decir que el punto (R´) es también un punto cualesquiera perteneciente a la recta (X´X) y ubicado a la izquierda de (O), esto hace que el segmento dirigido (OR´) posea longitud negativa de (x´) unidades, por lo que podemos decir, que dicho punto (R´) corresponde al número negativo (x´), de esta forma podemos afirmar que cualquier número real (x) puede ser representado por cualquier punto (R) de la respectiva recta (X´X), pero también es posible decir, que cualquier punto (R) sobre la recta (X´X) pudiera representar un determinado número real (x), en donde su valor numérico estará representado por la longitud del segmento (OR) y su signo será positivo si el punto está a la derecha de (O) y negativo si está a la izquierda de (O), por ejemplo:

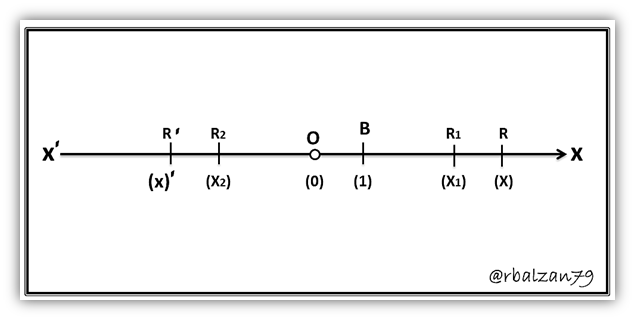
De esta manera hemos elaborado un sistema coordenado lineal o unidimensional, en donde pudimos establecer una correspondencia biunívoca entre los números reales y puntos de una recta, en donde resumiendo la figura de nuestro ejemplo, la recta (X´X) se denomina eje, el punto (O) representa nuestro origen, la coordenada de nuestro punto (R) está representada por el número real (x), podemos concluir diciendo que en el sistema coordenado unidimensional a cada número corresponderá uno y únicamente un punto sobre el eje, y de manera análoga podemos decir que a cada punto del eje le corresponderá uno y solamente un número real, por lo que el Punto (R) junto a su coordenada (x) constituyen la representación geométrica del número real (x) y en donde la coordenada (x) constituye la representación analítica del referido punto.

Para poder determinar la longitud numérica de un segmento el cual une dos puntos dados, para el caso de un sistema unidimensional por ejemplo; R1(x1) y R2(x2), resaltando que en geometría analítica se dice que dos puntos están dados cuando conocemos sus coordenadas, entonces, para nuestro ejemplo tanto x1 y x2 son conocidos, por lo tanto, la distancia que existe entre dos puntos lo podemos definir como el valor numérico o valor absoluto de la longitud de un determinado segmento el cual une a los dos puntos involucrados, ejemplo:

Sistema coordenado en el plano:

Como pudimos notar en un sistema coordenado lineal los puntos se encuentran restringidos sobre una recta, la cual hemos denominado eje, claramente si deseamos profundizar nuestro estudio hacia figuras más complejas como el estudio de las propiedades de los puntos de un triángulo, cuadrado, rombo, circunferencia, entre otras, nos encontraríamos muy limitados para la aplicación de un análisis de las propiedades geométricas sobre tales figuras antes mencionadas.

Esto nos lleva al estudio de un sistema coordenado con mayor libertad en donde un determinado punto pueda moverse en distintas direcciones pero siempre dentro de un plano, por lo tanto, el sistema que nos permita esta característica es el que conocemos como sistema coordenado bidimensional o plano cartesiano utilizado por la geometría analítica plana.

Ya hemos dados algunos pasos importantes antes de poder llegar a este punto, sobre todo pudimos estructurar y conocer las propiedades de un sistema coordenado unidimensional el cual será parte de la estructura de este sistema coordenado pero en este caso será con dos dimensiones, es decir, dos ejes perpendiculares entre sí.

Este tipo de sistema está conformado por un par de rectas dirigidas (X´X) , (Y´Y), denominadas ejes de coordenadas, las mismas son perpendiculares entre sí como ya se había expresado, donde la recta (X´X) la llamamos eje X, mientras que a la recta (Y´Y) eje Y; y el punto donde se intersectan lo denominamos origen (O). Mediante la intersección de estos ejes coordenados se origina una división del plano en cuatro regiones denominadas cuadrantes, en donde la dirección hacia la derecha del eje X representa el sentido positivo, mientras que para el eje Y el sentido positivo es hacia arriba, ejemplo:

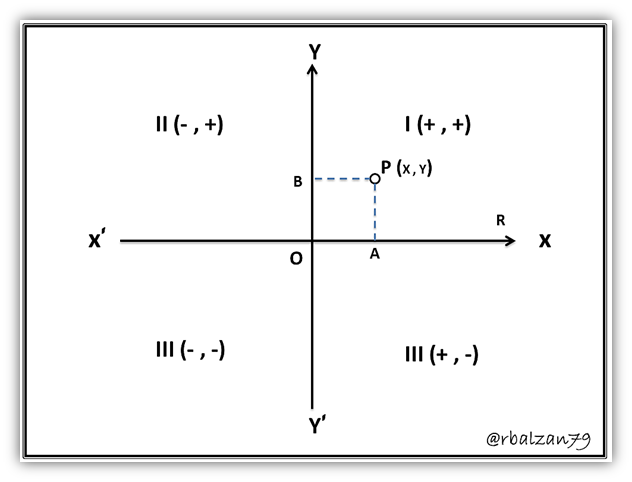
Recordando que para el sistema coordenado unidimensional a cada número le corresponderá uno y solo un punto sobre el eje, así de igual manera podemos decir que a cada punto del eje le corresponderá uno y solamente un número real, para este tipo de sistema tenemos que para cada punto (P) del plano coordenado le corresponde uno y únicamente un par de coordenadas (x,y) de manera análoga para un determinado par de coordenada (x,y) representara solamente un punto en dicho plano cartesiano, en la geometría analítico se ha establecido un orden para escribir el par de coordenadas, se escribe en primer lugar la abscisa (X) y después la ordenada (Y) en segundo lugar, por tal razón el par de coordenadas en un plano lo denominamos par ordenado de números reales.

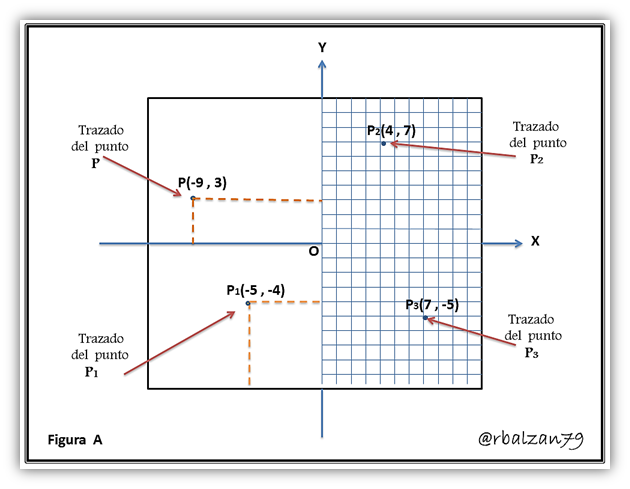
Es importante destacar que generalmente de forma práctica realizamos cualquier gráfica en el plano mediante cualquier tipo de papel u hoja en blanco como podemos observar en la figura (A) lado izquierdo, pero es necesario que los estudiantes en sus inicios utilicen papel milimetrado con la finalidad de obtener mayor precisión en el trazado de los puntos, ya que un pequeño error de proporcionalidad podría dificultar la elaboración de una representación gráfica, generando confusión y desanimo en el estudiante.

Cuando localizamos un punto cualesquiera en el plano utilizando sus coordenadas, esta acción la denominamos trazado del punto, como lo hemos realizado en la figura (A) del ejemplo anterior.

Funciones afines y lineales, la recta en el plano:

Una vez estudiado el sistema coordenado bidimensional o plano, es importante realizar el estudio de la recta y otras figuras en tal sistema, una de las características más importantes de la geometría analítica, es poder estudiar las propiedades de las figuras geométricas más allá de una idealización de sus formas.

Mediante la geometría analítica hemos podido establecer una correspondencia entre las funciones definidas en aspecto o términos de expresiones algebraicas y los objetos geométricos, por lo tanto, una función afín cuya expresión algebraica sea de la forma y = mx + b corresponderá a una línea recta al referir sus puntos en el plano a un sistema coordenado bidimensional o cartesiano, y que particularmente también una función lineal cuya expresión algebraica de la forma y = mx representa la ecuación que corresponda a una determinada recta que pasa por el origen del sistema coordenado cartesiano, ejemplo:

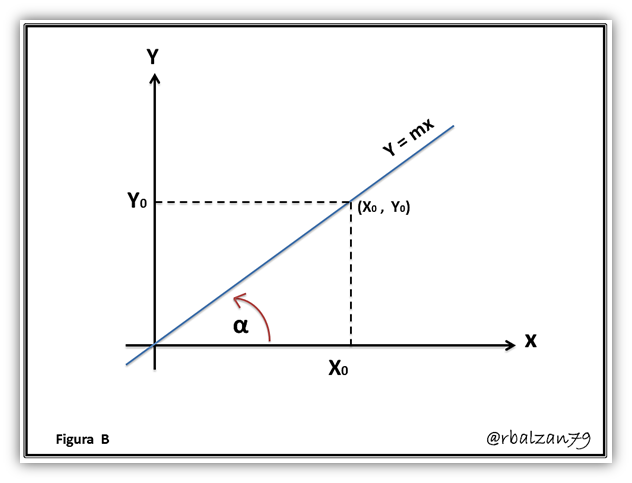
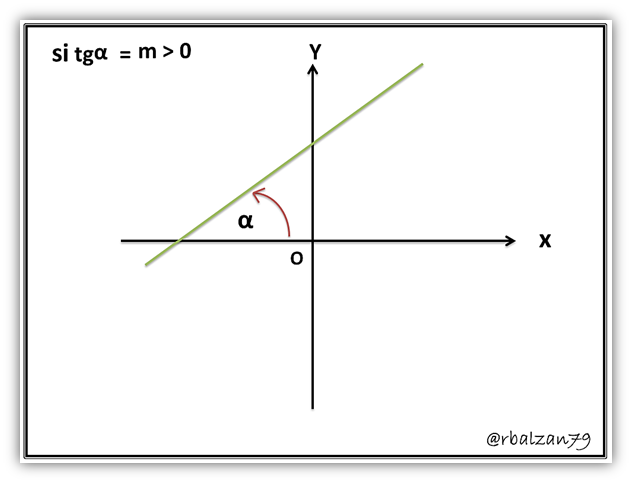
Podemos notar que en la figura (B), una determinada recta que tiene la forma de la ecuación y = mx, forma un ángulo con la dirección positiva del eje de las abscisas o de las X, en donde cualquier punto (x, y) de dicha recta podrá cumplir con la condición:

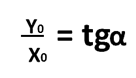
Y como y0 = mx0 tenemos que en definitiva m = tgα, esto también se cumplirá para una recta que posea ecuación general y = mx + b; donde b representa la ordenada que corresponde al punto de intercepción de una determinada recta con el eje de ordenadas o eje de Y, ejemplo:

Observamos en la figura (B) que para cualquier punto (x,y) de dicha recta se podrá cumplir lo siguiente:

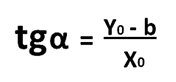
Por lo tanto, si tenemos en cuenta que y0 = mx0 + b, tendremos en definitiva:

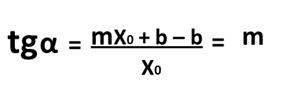
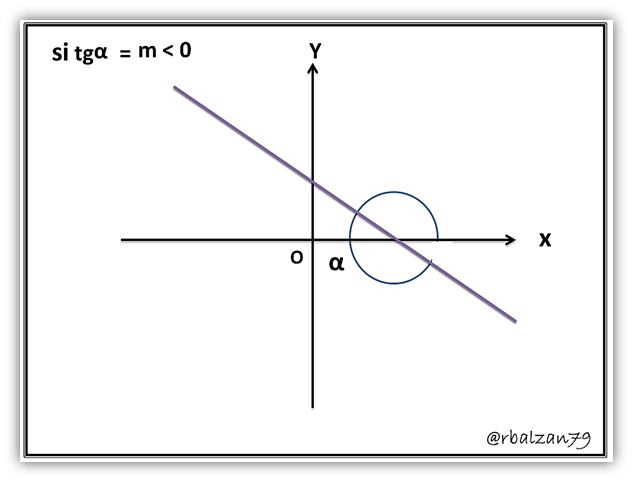
Entonces el coeficiente (m) de nuestra variable independiente será el valor de la tangente trigonométrica de dicho ángulo α, el cual se forma mediante la intersección de la recta con el eje horizontal o eje de las abscisas, es por esto que a (m) la llamamos pendiente de la recta, ya que mide la inclinación respecto a dicho eje horizontal, es importante destacar el comportamiento de dicha tangente trigonométrica ya que será positiva cuando los ángulos están situados tanto en el primer como tercer cuadrante, y será negativa para los ángulos situados en el segundo y cuarto cuadrante, y para la ubicación de la recta con respecto a los ejes coordenados no los dirá el signo de la pendiente o coeficiente (m).

Método gráfico para solucionar un sistema lineal de dos ecuaciones y dos incógnitas (2x2):

La geometría analítica haciendo uso del lenguaje algebraico pone de manifiesto ciertas ecuaciones de este tipo (algebraicas) las cuales corresponden a figuras geométricas, para este caso dos rectas interpretadas por una expresión algebraica (ecuación) con la finalidad de poder brindar la solución (si la tiene) de un determinado sistema lineal de ecuaciones 2x2, esto haciéndolo equivalente a un problema de hallar la intersección de dos rectas, dicho procedimiento lo hemos denominado método gráfico, inicialmente debemos despejar la variable y de ambas ecuaciones para luego crear una tabla de valores para cada expresión obtenida después de despejar a y, por lo tanto, consideremos el siguiente sistema de ecuaciones lineales:

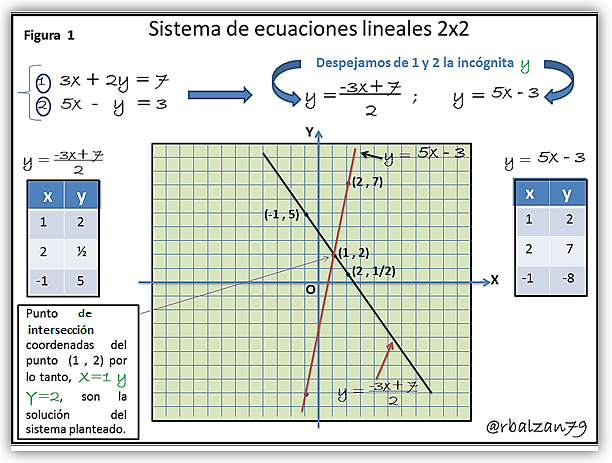
Podemos resaltar que hemos obtenido mediante el método gráfico el resultado de dicho sistema relacionándolo con la intersección de dos rectas antes descritas por las expresiones obtenidas despejando a y, para resolver estos sistemas 2x2 conocemos los métodos de sustitución, igualación y reducción, por lo tanto, podemos a través de cualquiera de ellos comprobar el resultado arriba descrito, sin embargo, para profundizar en la aplicación de tales métodos les dejo el enlace de una de mis publicaciones donde analizamos la aplicación de los mismos, Ajuste de ecuaciones químicas.

Conclusiones:

• La obtención de un determinado conocimiento pasa por el hecho de ubicar las herramientas conceptuales y prácticas adecuadas para tal fin, pero necesario es poder ir paso a paso con la finalidad de armar una adecuada estructura de los saberes mediante el maravilloso camino del aprendizaje, debemos aprovechar cada aspecto positivo que podamos encontrar en nuestro recorrido, por lo que es vital evaluar o conoce la serie de conocimientos previos que podamos encontrar en nuestros estudiantes, por lo tanto, es importante siempre resaltar el grado de atención que podamos lograr de ellos, esto fortalece sin dudas la combinación binomial docente-estudiante logrando elevar tanto el entusiasmo como el interés del docente por enseñar así como del estudiante por aprender, a pesar de parecer repetitivo lo antes expuesto estoy convencido que el éxito de un determinado aprendizaje se fundamenta en la atención y en el entusiasmo tanto del docente como de sus estudiantes.

• El haber conocido el aspecto básico de un segmento rectilíneo desde el punto de vista de la geometría elemental, nos permitió poder dar nuestros primeros pasos, ya que el mismo representa una porción de una determinada recta, constituyéndose entonces como un subconjunto de puntos de dicha recta, pero que a través de la geometría analítica le hemos podido dar a esta figura geométrica mayores características y propiedades tales como dirección y sentido (orientación), además con la firme intención de poderlos utilizar para la consolidación de conceptos muchos más complejos, además mediante la geometría analítica le asignamos a las longitudes de un segmento rectilíneo dirigido la característica de positivo o negativo esto dependerá de la aplicación que deseamos darle mediante la realización de un estudio a cualquier figura geométrica.

• Debido a la inyección analítica a las propiedades o características de un segmento nos llevó a la construcción de un sistema coordenado lineal o unidimensional, donde logramos establecer una adecuada proporcionalidad entre un punto geométrico y un determinado número real, sentando las bases de esta manera para otros tipos de sistemas coordenados con mayores dimensiones como la del plano y el espacio.

• El sistema coordenado bidimensional o también conocido como plano cartesiano se ha constituido como una de las más útiles de las herramientas que la geometría analítica plana nos ha brindado, mediante el plano hemos podido estudiar las características y propiedades de figuras geométricas más complejas (circunferencia, rectángulos, rombos, triángulos, elipse, entre otras), además mediante la utilización de expresiones algebraicas las cuales representan funciones como para la recta.

• La geometría analítica plana desde el mismo momento de su llegada se convirtió en un maravilloso instrumento necesario para la comprensión de las formas o figuras geométricas, mediante el plano cartesiano o bidimensional empezamos el estudio de la recta, esta figura geométrica nos proporcionó importantes propiedades como pendiente y ángulos, con la ayuda de la interpretación trigonométrica y el álgebra, dichas propiedades o características juegan hoy en día un papel fundamental en áreas como el cálculo y en consecuencia en la ingeniería y de igual forma para la arquitectura.

• La geometría analítica plana, permite que las ecuaciones o expresiones algebraicas correspondan a figuras geométricas, ya que mediante la ecuación de la recta es posible el estudio de las mismas en el plano, pero además nos ha permitido interpretar la solución ( si la tiene) de un determinado sistema de ecuaciones lineales relacionándolo con un planteamiento equivalente al de poder hallar la intersección de dos rectas, el cual lo denominamos analíticamente como un método gráfico, esto es lo que ha caracterizado a la geometría analítica, la profundización del estudio de cualquier figura geométrica en sus distintas dimensiones.

• Mucha tela que cortar y compartir pero podemos ir paso a paso para una mejor comprensión de las distintas áreas tanto de la geometría como de las matemáticas en general, los espero en la próxima entrega o parte sobre el estudio de esta magnífica herramienta practica como lo es la geometría analítica plana, para poder avanzar hacia otros conocimientos más profundos y complejos en los distintos ámbitos de las matemáticas.

Nota: Todas las imágenes fueron elaboradas en paint y power point 2010 para Windows7.

Referencias Bibliográficas:

• Charles H. Lehmann. Geometría Analítica. Décima tercera reimpresión. Editorial Limusa. México, D.F. 1989.

• Jennings, G.A. Geometría moderna con aplicaciones. Springer, New York, 1994.

• Snapper, E., Troyer, R.J. Geometría afín métrica. Dover, New York, 1971.

Autor: @rbalzan79