El estudio de las fuentes ópticas representa una de las partes más cruciales e importantes en los diseños de sistemas por fibras, precisamente las fuentes son los elementos activos dentro de la etapa de transmisión, es decir, estos dispositivos serán los portadores de la información los cuales “traducirán” en energía fotónica el flujo de datos en cuestión , por ello es preciso dominar a un nivel más o menos específico lo que sucede en el interior de estos aparatos electrónicos; en esta primera entrega de la serie referente a la Fuentes Ópticas se estudian los principios cuánticos (comportamiento luminoso sobre los materiales) que hacen posible la correcta actividad de las fuentes ópticas así como el reconocimiento de los materiales semiconductores empleados para su elaboración.
En primera instancia, las fuentes que se emplean para la transmisión deben cumplir con ciertos requisitos, el que se asume de manera más inmediata e intuitiva es que las longitudes de ondas generadas por las fuentes deben coincidir con las ventanas de transmisión (850nm, 1310nm, y 1550nm); otro aspecto relevante es que las dimensiones de las fuentes sean equiparables a las reducidas longitudes de la fibra y por supuesto, para que la eficiencia en el sistema se maneje de forma más optimizada , la anchura del espectro de una fuente debe lograr ser relativamente “pequeña” para que los efectos por dispersión no sean críticos en la comunicación.
Profundizando en aspectos más técnicos (y antes de asumir de lleno las fuentes ópticas), se analizan los fenómenos de la interacción radiación-materia, los cuales describen la generación y detección de fotones, pero primero se plantean los niveles de Energía E1 y E2 donde se encuentran los electrones cuyas transiciones provocan el meollo del asunto:
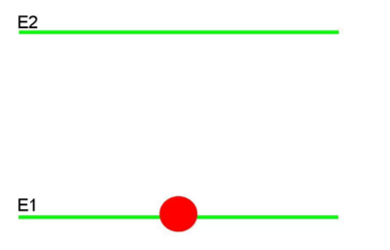
Figura 1 Niveles de Energía E1 y E2 Fuente
La pelotica roja representa un electrón, y este puede estar tanto en E1 como en E2
La luz al incidir en la superficie de un material, por naturaleza conlleva a que el campo electromagnético propiamente dicho, genere ciertos efectos, estas perturbaciones se denominan: emisión espontanea, emisión estimulada y absorción ; de forma general, se pueda asumir como una alteración a las partículas de dicho material, alteraciones que precisamente conllevan a la transición de electrones a distintos niveles de energía (como se hizo mención en una entrega anterior). La materia prima que gobierna la fabricación de fuentes ópticas son los materiales semiconductores, por tanto, los niveles de energía que se mencionaban previamente para este caso serán “La Banda de Valencia y la Banda de Conducción”.
Para determinar la cantidad de estos electrones que se alojan en dichos niveles, se emplea la estadística de Boltzman:
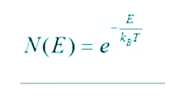
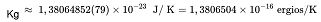
E representa el valor de ese novel de energía, Kg o K según la bibliografía , es un valor constante denominado constante de Boltzman y T es la temperatura. La estadística de Boltzman nos servirá más adelante.
De lo anteriormente dicho, se define entonces a la emisión espontanea como un proceso de carácter aleatorio, pues dado dos niveles de energía, en los cuales tendremos lógicamente dos poblaciones de electrones, de manera arbitraria (o espontanea como su nombre lo indica) un electrón en el nivel más alto sufrirá una transición al nivel inferior y por consecuencia se producirá un desnivel energético que puede ser calculado de la siguiente manera:
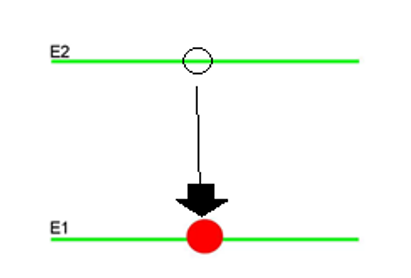
Figura 2 Transición de un electro de E1 a E2 , adaptado por @vjap55 de la fuente Fuente
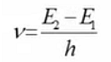
Es decir, la frecuencia del fotón resultante v , será la diferencia de estos niveles de energía dividido por la constante de plank h, dado entonces que la fase del campo electromagnético está asociado a niveles de incertidumbre muy altos, se dice que la radiación es no coherente, pues no se sabe con exactitud los parámetros que componen a la onda en cuestión , lo que se pudiera hacer es determinar una tasa de emisión espontanea tomando en cuenta las variaciones que tienen las poblaciones de electrones en el nivel más alto con respecto al tiempo, en efecto esta tasa será proporcional a lo que se denomina coeficiente de Einstein de esta misma emisión :
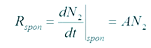
Por otra parte y en relación a lo antes mencionado, el fenómeno que explica el funcionamiento de los detectores ópticos, es conocido como fenómeno de absorción, en esta oportunidad, imagine que dado los niveles de energía que se presentaron anteriormente, y al aplicar un campo electromagnético a el nivel inferior, cuya energía está definida por la ecuación que asocia la diferencia de energética de dichos niveles, el fotón al ser absorbido por el material , provoca que un electrón se pase de la banda de valencia a la banda de conducción, una observación que se puede hacer , es que el campo electromagnético que oscila o atraviesa dichos materiales conduce a que su potencia efectiva se vea reducida.
Como en el caso anterior, la tasa de absorción se calcula como una variación temporal en el nivel más bajo, y además de ser proporcional a la población de este nivel, será proporciónala a la densidad espectral de la radiación incidente.
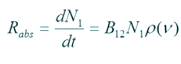
Y finalmente , la emisión estimulada tiene su interpretación en la situación que las partículas se encuentran en el nivel más alto y dada la incidencia de un conjunto de fotones, producirá la transición de un electrón al nivel energético más bajo , como consecuencia se liberara más energía equivalente a la resta de E1 Y E2, se tendrá entonces un fotón adicional por cada fotón incidente con propiedades bastante similares, en este caso la radiación se dice que es coherente, pues el nuevo fotón tendrá energía, frecuencia y fase equivalente al fotón original, como en las dos situaciones previas, la tasa de emisión estimulada se cuantifica como la variación temporal de la población en el nivel más alto, de igual manera, será proporcional a la densidad electromagnética incidente:
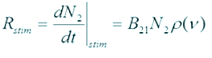
Una fuente óptica se entiende por lo general como un material en equilibrio termodinámico, es decir, que el número de las partículas en los dos niveles son equivalentes o constates, por consecuencia el número de las transiciones que sufren los electrones de un nivel a otro también serán iguales, dicho de forma matemática, la suma de la tasa de emisión estimulada y la tasa de emisión espontanea es igual a la tasa de absorción:
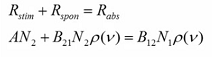
Sustituyendo las expresiones de las poblaciones para cada nivel, la cual fueron inducidas por la estadistica de Boltzman, se tiene entonces que:
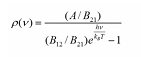
Esta expresión resultante es una relación que cumple cualquier campo electromagnético, es decir, que esta fórmula verifica la densidad espectral de la radiación de cualquier campo.
Para entender mejor como se relacionan los coeficientes de Einstein de absorción y emisión, comparamos la expresión recién expuesta con la razón que define la radiación de un cuerpo negro:
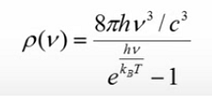
"Un cuerpo negro, es un material u objeto capaz de absorber toda la radiación que se le es suministrada sin que este refleje absolutamente nada , la radiación electromagnética que emiten estos cuerpos es debida únicamente a la temperatura de dicho cuerpo."
Figura 3 Cuerpo NegroFuente
Comparando las expresiones se puede observar que los coeficiente B12 y B21 son iguales, por su parte el coeficiente A de Einstein se relaciona con una constante que depende de la frecuencia de B :
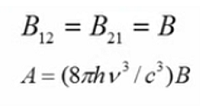
En concreto, esta es una función de la frecuencia y de la temperatura.
Pues bien, ¿a qué se debe todo este bosquejo teórico?, en efecto, con esta revisión de los principios termodinámicos se puede comprender el funcionamiento de una fuente óptica cuando es accionado su LED o Láser; para concluir con este apartado, se ejemplifican con algunos valores las ecuaciones resultantes que se han expuesto:
En condiciones normales, a temperatura ambiente :298°K, se puede calcular el producto con constante de Boltzman :
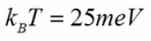
Y para el caso de una longitud de onda de 1 micra, se calcula el termino de la constante de plank por la frecuencia:
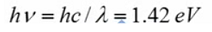
Por tanto, en condiciones de equilibrio termodinámico , el termino hv es mucho mayor que la constante de Boltzman por la temperatura:
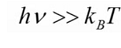
Entonces esto conlleva a que en condición de equilibrio, la emisión espontanea es predominante:
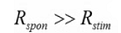
Materiales
Como se dijo previamente, las fuentes ópticas son en esencia materiales semiconductores; recordar que un material semiconductor es aquel cuyas propiedades eléctricas se intermedian entre las propiedades de los conductores y los aislantes , poseen una estructura cristalina donde los grupos de átomos se distribuyen sobre un patrón especial denominado “red” ; en este texto no se pretende realizar una revisión exhaustiva de este tema, se recomienda la lectura de los artículos de @iamphysical y @carloserp-2000 , quienes profundizan en detalle el estudio de semiconductores.
Sabiendo entonces que una fuente es compuesta por materiales semiconductores, se proceden a especificar concretamente los materiales usados para la fabricación:
Para el caso de la primera ventana ubicada en los 850 nm se emplea Arseniuro de Galio, en muchas de sus implementaciones, se sustituyen algunos átomos de galio por aluminio, en la siguiente expresión X, representa esa porción molar de Aluminio :
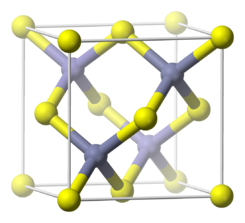
Figura 4 Estructura del Arseniuro de galio-aluminioFuente
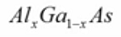
De igual manera para la 2da y 3era ventana se usan el Arseniuro de galio, en esta ocasión el dopaje se realiza intercambiando los átomos de Galio por Indio y el Arsénico por fósforo, I representara la fracción de Indio:
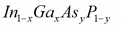
Estrictamente hablando las fuentes ópticas son uniones del tipo P-N, concretamente, una unión P-N en hetereoestructura , en otras palabras, se necesitan varios materiales de la misma familia y para evitar la presencia de defectos que puedan reducir la eficiencia cuántica de la fuente, sus propiedades de red deben ser similares, he allí entonces la mención de estos semiconductores, pues la familia de arseniuro de galio con indio y fosforo cumplen con la concentración molar I la cual presenta una constante de red uniforme.
Habiendo abordado los principios y materiales de las fuentes ópticas, se puede entonces develar las formas de radiación específica que son utilizadas, es decir coherente y no coherente, o LED y Laser, estos temas serán bien definidos en las próximas entregas. Espero les sea útil y sobre todo les sea su agrado.
Referencias
Optical Fiber Comunications ; Gerd Keiser (2008)
Fuentes Ópticas - Comunicaciones Opticas
Material Audiovisual variado de la Universidad Politécnica de Valencia( UPV) ; MOOC Fundamentos de Comunicaciones Ópticas
