FUNCIONES DE BESSEL Y SUS APLICACIONES EN LAS TELECOMUNICACIONES Y ELECTRODINÁMICA

¡Hola amigos steemit!

En el análisis de algunos sistemas físicos encontramos Ecuaciones Diferenciales que presentan particularidades especiales debido a su complejidad, tal es el caso de la Ecuación Diferencial de Bessel cuyas soluciones son conocidas como las Funciones de Bessel.

Las funciones de Bessel juegan un papel fundamental en la solución y entendimiento de problemas en distintas área de la Física e Ingeniería.

Los modos de propagación de las ondas electromagnéticas en cavidades cilíndricas, tales como Coaxiales o Fibras ópticas, la propagación de calor y los Espectros de Frecuencia de una Modulación Angular son algunos de los casos donde encontramos el aporte de las funciones de Bessel.

Figura 1. Biografía de Friedrich Wilhelm Bessel
Fuente

ECUACIÓN DIFERENCIAL DE BESSEL

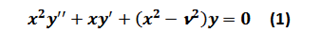
La solución de la ecuación de Bessel para cualquier valor de "ν" obtenida a través del método de series es de la forma:

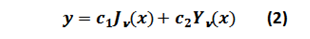
Donde:

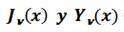➞ Se conocen como las Funciones de Bessel de primera clase y segunda clase respectivamente y están dadas por las Ecuaciones:

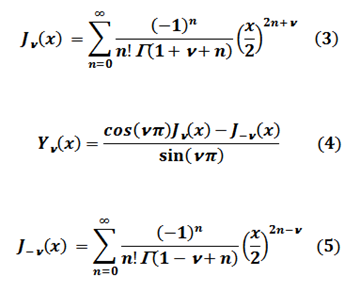
Γ ➞ Función Gamma

REPRESENTACIÓN GRÁFICA DE LAS FUNCIONES DE BESSEL

Figura 2. Representación Grafica de la Función de Bessel de Primera clase.
Fuente

Figura 3. Representación Gráfica de la Función de Bessel de Segunda clase.
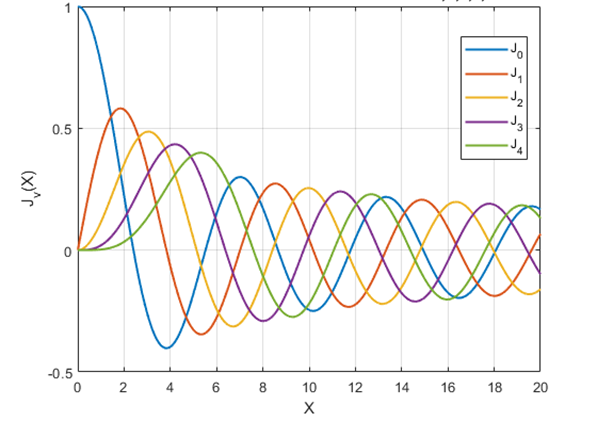
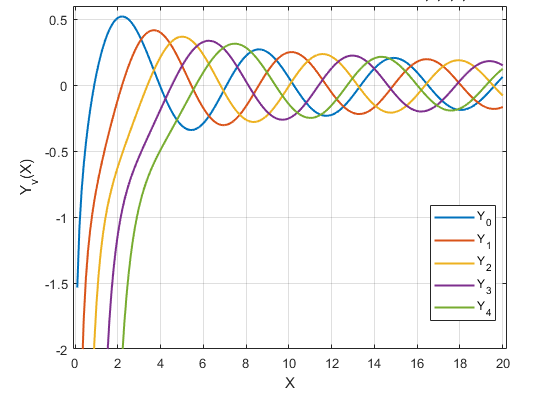
Fuente

En la representación gráfica de la funciones de Bessel de segunda clase, también conocidas como funciones de Neumann se puede observar que estas tienden al infinito cuando (x→0).

Debido a esta tendencia en muchos sistemas esta solución es desechada ya que carece de sentido físico.

APLICACIONES

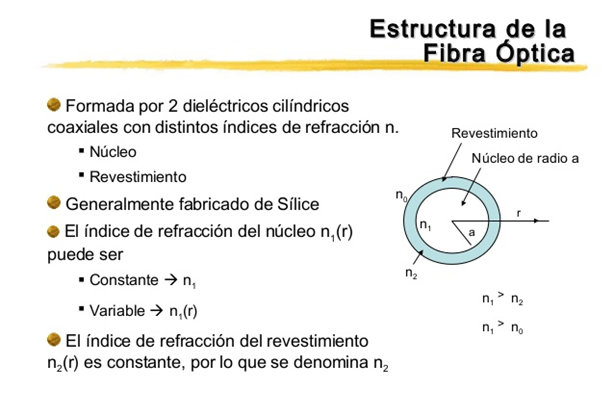
FIBRA ÓPTICA

En una cavidad cilíndrica el potencial "Φ " en su interior esta descrito por la Ecuación de Laplace según la expresión:

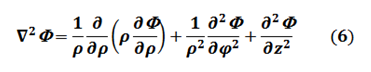
REGIÓN CILÍNDRICA

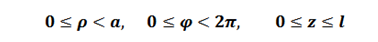
La solución de (6) por el método de separación de variables es de la forma:

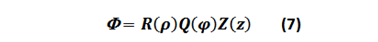
Cada una de las soluciones R(ρ),Q(φ) y Z(z) es gobernada por las Ecuaciones diferenciales:

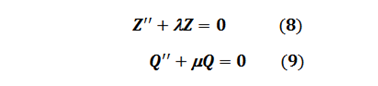
λ, μ ➞ constantes.

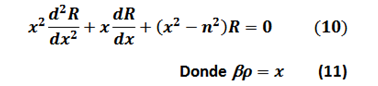
Las Ecuaciones Diferenciales (8) y (9) muestran el comportamiento de la onda en la direcciones de Z y φ y cuya solución es obtenida a través de métodos relativamente simples.

Estas soluciones son de la forma:

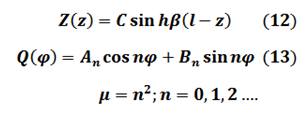
La Ecuación diferencial (10), la cual gobierna el comportamiento radial de la onda, es una Ecuación Diferencial de Bessel y su solución está dada por la expresión:

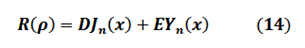
En una Fibra óptica la ecuación (14) se expresa de la forma:

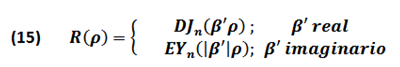
Donde:

n₁ ➞ indice de refracción del núcleo
n₂ ➞ indice de refracción del revestimiento
k₁ ➞ magnitud del vector de onda en el núcleo
k₂ ➞ magnitud del vector de onda en el revestimiento

Figura 4
Fuente

El comportamiento de las ondas en cavidades cilíndricas descrito por las funciones de Bessel ha contribuido en el diseño y operatividad de fibras ópticas las cuales han permitido la transmisión de señales en un amplio rango de frecuencias.

MODULACIÓN EN FRECUENCIA (FM)

La modulación consiste en la transmisión de una señal (mensaje) usando para este fin una señal portadora. La modulación en frecuencia es un tipo de modulación angular en el que la señal mensaje “m(t)” es proporcional al ángulo de fase .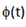

La señal modulada en ángulo es de la forma:

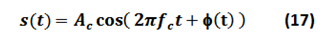
En FM:

Si el mensaje que se desea transmitir es de la forma:

Donde:

“β” es conocido como el índice de modulación.

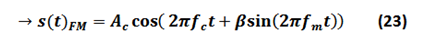
El espectro de la señal (comportamiento en frecuencia) es un requerimiento en el análisis de transmisión de señales. Dado que la Modulación en Frecuencia es no lineal, su espectro no puede ser obtenido a través de una Transformada de Fourier.

La transformación a Frecuencia es evaluada numéricamente en términos de la función de Bessel a través de la Ecuación.

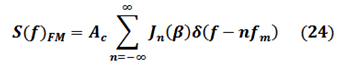
En la ecuación (24) se observa que las amplitudes del espectro de una señal FM son controladas por la función de Bessel de primea clase. (Ver Figura 5).

Figura 5. Espectro de Bessel de una señal FM
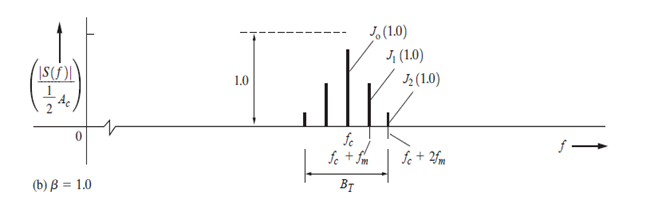
Fuente: Sistemas de comunicación digital y analógico. León W. Couch-7ma-edición.

Figura 6. Coeficientes de Bessel Tabulados para valores de β entre 0 a 15
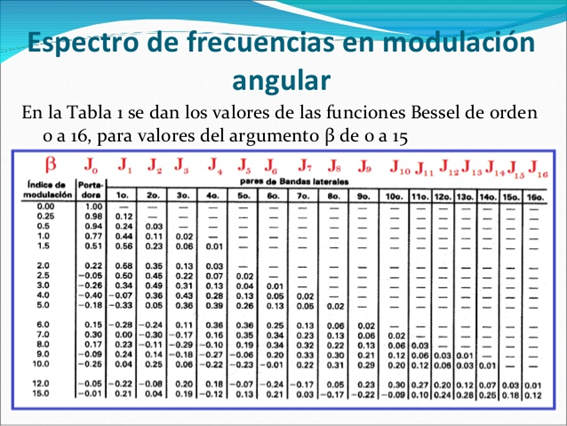
Fuente

REFERENCIAS

• Ecuaciones Diferenciales con aplicaciones de modelado. Dennis G. Zill. 6ª edición.

• Sistemas de Comunicación Digital y Analógico Leon.W.Couch, 7ma-edición.

• Teoría Electromagnética. William. H. Hayt, John. Buck.

• http://la-mecanica-cuantica.blogspot.com/2009/08/aspectos-matematicos-de-las-ondas.html.

• http://aprendiendoingenieriaquimica.blogspot.com/2016/02/conduccion-de-calor-en-regimen.html.

• https://es.slideshare.net/machas94/ecucacion-de-bessel.