Engineering Slut || How Bernoulli's equations could solve engineering problems

You might be riding a big hell of a car, having an attention catching home and in general, living a very romantically luxurious life but well, trust me, we are living in an imperfect world – to put it simple. I mean no matter how hard you try to solve a problem, or prevent one from happening, things still go wrong. It is the way of life. And sometimes, it means your basement or the whole city gets flooded. Heavy rain might claim the credit but who cares? Damn it! Let the dude have his way.

Source: Pixabay (Public domain - CCO licensed)

But when things get this messy, what do you do? You need to get the water out, right But how?

Well, you are going to need some equipment. Some pipes. A pump. And to choose the right pump for the job, you will need Bernoulli's principle. As a budding engineer, I believe you already know about fluid mechanics and the energy transfers involved. But engineering is about more than just learning - It is also about using your knowledge to build things and solve problems. Like your flooded basement or house.

To get the water out, you will need a pump - a device that is used to move liquids, compress gases, or force air into things like tires. In this case, obviously you will want a pump that is designed to move liquid and powerful to push all that water in the basement somewhere else, like outside, perfectly far away. You could just pick a random pump and hope it works, but that is not the engineering way.

To do this properly, you can calculate how powerful your pump needs to be with the help of 18th century Swiss mathematician - Daniel Bernoulli. There were actually eight mathematicians in the Bernoulli's family in the 17th and 18th centuries, including Daniel's father and two brothers. His father was especially jealous of his success. Their rivalry was so bad that when the two of them jointly won a scientific prize, his father banned him from the house. He also went on to plagiarize Daniel's later work, changing the date so it seemed like he had actually published it before his son.

As competitive as their relationship was, it is possible that the challenge pushed the younger Bernoulli to become a better innovator and mathematician. But either way, he discovered a god deal about fluid flow in his life. He specifically wanted to understand the relationship between the speed at which blood flows and its pressure. So to learn more, he conducted an experiment on a pipe filled with fluid.

Bernoulli noticed that when he punctured the wall of the pipe with an open-ended straw, the height at which the fluid rose in the straw was related to the pressure of the fluid in the pipe. Soon, physicians all over Europe were measuring their patient's blood pressure by sticking sharp glass tubes directly into their arteries. Luckily for us, they have developed more gentle methods.

But while the physicians of his day were being quite the pain in the arm, Bernoulli was onto something very important. He realised that energy has conserved in a moving fluid. It could be converted between different forms like kinetic - the energy of motion and potential energy, but the total energy within the fluid will stay the same. So if one form of energy decreases, for example, like if the fluid slows down, there has to be a corresponding increase in another form of energy so the total remains constant.

Bernoulli’s principle

Bernoulli's insight is that energy could also be converted between kinetic and potential energy and pressure. Today, this is known as Bernoulli's principle and it states that

As the speed of fluid is flowing horizontally increases, the pressure drop will decrease and vice versa.

This means that the fluid's speed will have an inverse relationship with its pressure, or, as one arises, the other falls.

Now this principle only applies to what is known as an isentropic flow, meaning it doesn't involve any heat transfer and its reversible, so it can go back to its initial state with no outside work. Or at least, close enough that you can neglect the effect of heat transfer or irreversibility.

To keep things simple, we will assume this applies to our system. For Bernoulli's principle, the fluid also needs to flow horizontally, or not have a drastic change in height, because it doesn't consider the effects of gravity. So to account for height and gravity and apply Bernoulli's principle to the design of our pump system, we are going to need more general equation - The Bernoulli's equation.

The Bernoulli's equation

There are many forms of Bernoulli's equation. But the one we will look at in this post relates to pressure, speed, and height of any two points in a steadily flowing fluid with a density p. Since something’s density is just its mass divided by its volume, this equation actually works out really neatly: On both sides of the equation, you can see that we are defining a point's total energy per unit volume by its pressure, plus its kinetic energy per unit volume, and then finally adding its potential energy per unit volume.

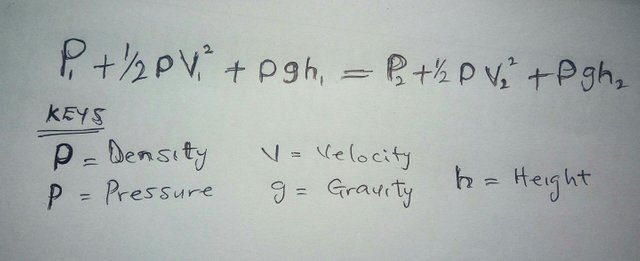
Basically, this equation says that the total energy of the first point is equal to the total energy of the second point. So, if the two points have different speeds, it makes sense that they have different pressure and potential energy to balance off the equation. This potential energy will be the same at every point of the equation and also gets us the equation in this format:

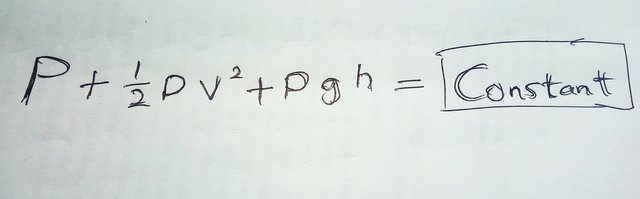
It is very similar to what we had before, but since the total energy will always be the same, you can replace the right side of the equation which represents the total energy at the second point of the pipe with constant. That is much simpler. And it gets even simpler if the fluid only flows horizontally. In other word, if there is no change in height between the points we are comparing. That means we can cancel out the potential energy, leaving us with only the pressure on the kinetic energy uniformly equal to constant.

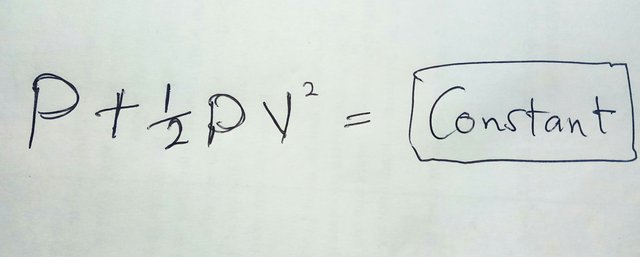
Right now, you are probably wondering how we can find out the actual value of this constant we are talking about. Well, we know that the total energy of the given volume and one way to find it is to add up the pressure, kinetic energy over volume and the potential energy of the volume.

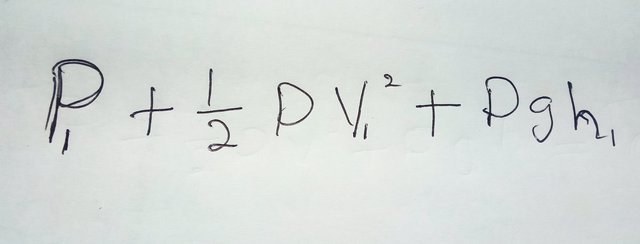
Some stuffs we need to take into account

When we talk about a life scenario with the pumping vault, we have to take into account, the energy that has been put into, and lost from the system to move the fluid. We said that this energy can take two forms - work and heat. Work is what is driving the pump. That work is what is moving the water along and contributing to the total energy. But that is not the only factor. There is something else we need to take into account.

The other thing to take into account is friction. As the water flows through the pipe, the movement will induce stress I the fluid which causes friction. That silly resistance you get when two things slide against each other. Friction makes a system to loose energy to heat, and there is going to be lot of it as the water rubs against the inside of the pipe.

Now, even with the pump, the total energy of the fluid will still be constant throughout the pipe. This means that the changes in energy from work to fiction will need to balance up with the changes to the three forms of internal energy. So, pressure, kinetic energy and potential energy. That is the only way the total energy will remain the same.

Going back to Bernoulli’s equation, we can now modify it slightly. The first thing we need to do is rewrite it in terms of changes in energy. On the left side, there are changes to the entire form of energy, the change in pressure plus the change in kinetic energy per unit volume plus the change in potential energy per unit volume and that all equals to constant. Then we will need to divide the whole things by density which is really the same as multiplying the volume and dividing by mass.

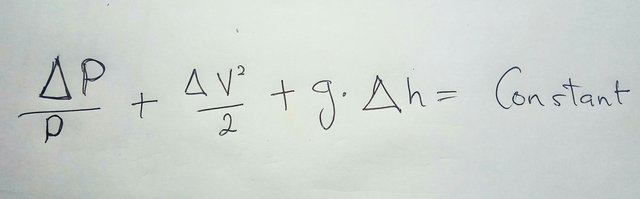
So now we are talking about overall change per unit mass throughout the flow instead of changes per unit volume. This is what we needs to balance out with energy added by the pump and lost to friction. So instead of the constant, we can now say that the left side of the equation is equal to W which is the work put in to achieve change the energy per unit mass minus frictional energy loss per mass.

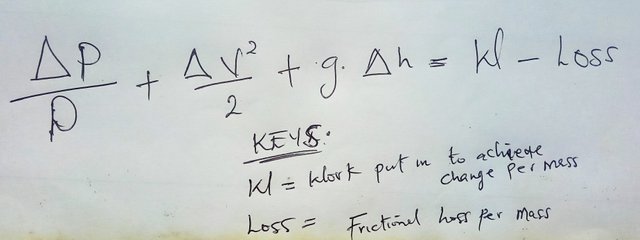
So many engineers will take this equation a step further and divide the whole thing by gravity, which gets us to the value known as H – the height to which the pump can drive the fluid.

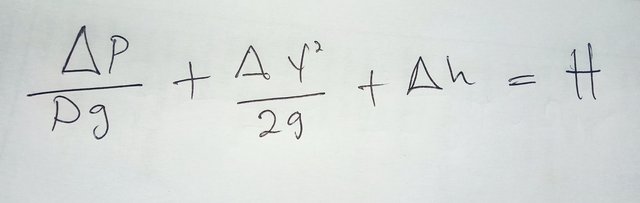
Now, the actual amount of energy lost to friction depends on a bunch of different parameters. One of the big ones is the velocity of the fluid. The greater this velocity, the greater the frictional loses. This makes sense if you think about it. It makes it much more intense at the side of the pipe, if the water is moving faster.

What increases friction here

The turbulent of fluctuating flow will increase the friction. The length of the pipe matters too. If there is more path for the water to rub against, it will loss more energy to friction. And then, there is roughness. The rougher the pipe, the more friction there would be.

To figure how perfect the pipe needs to be to get the water out of the basement. In another word, how much work it should be capable of producing, you have to account for all of these. You want to minimise friction by keeping the pipe as simple and as short as possible. This way, you won’t need much work to counter energy loss. The pump also needs to be able to perform enough work to account for the pressure velocity of water as well as any changes in elevation.

Conclusion

The reality tends to be a little messy of the simplified version Bernoulli’s equation we are using, but it should be enough to get a sense of which pump you need to finally clear out your basement. Who knows how much is going down right now? But generally, Bernoulli’s equation is a good foundation for working with fluid and figuring out how to build designs of our own.

---

References

• Bernoulli's principle
• Fluid dynamics
• Friction

---

Join other STEM writers on Discord and keep using the #steemstem tag for STEM related posts. Join the Nigerian STEm writers here