In a previous post on Tauchain I discussed the idea that TML could be used as a SAT solver. I did not go into much detail on the concept of depth first search which is the common way SAT solvers work. I used the example of a Rubik's cube to illustrate how when you have a finite amount of states you can apply machine intelligence to brute force search through these states. This post will provide a bit more detail on the search algorithms which fall under "State Space Search".
State Space Search
Depth first search is a method of doing a state space search. All state space searches start at some initial state and are optimizing to research a desired state. The concept of a search space relates to the concept of solution space. There are usually a limited number of solutions to any problem. Any problem with multiple solutions can be optimized if you can find a way to compare all the solutions to each other in an attempt to rank the solutions. The highest ranked solution is the optimal solution to the problem.
The search space (solution space) can be traversed either algorithmic in the sense of depth first search for example or it can be traversed using a genetic algorithm. The genetic algorithm approach is the evolutionary computation approach which I stumbled upon as a means of solving problems . This evolutionary approach can be also highlighted as a universal Darwinistic approach to problem solving for those familiar with what universal Darwinism is.
Ohad in developing Tauchain appears likely to take an algorithmic approach due to his background in these areas. His approach to TML seems likely to lead to TML being implemented as a sort of SAT solver which more likely than not will apply a depth first search method. That is why I used the example of depth first search and because TML is likely to apply this I will give a brief discussion of depth first search.
Depth First Search
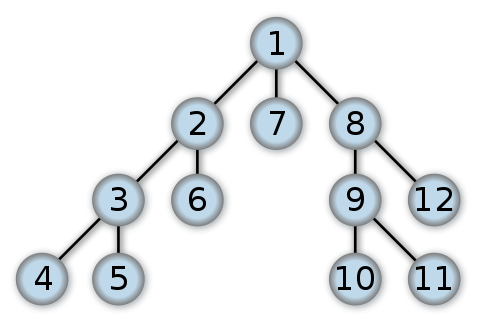
Alexander Drichel [CC BY-SA 3.0 (https://creativecommons.org/licenses/by-sa/3.0)]
To understand depth first you have to think of the tree. A tree can map out all the possible solutions to a problem. Note and this is very important that Ohad went with partial fixed point logic and that one of the goals of TML is to be capable of solving any P-space problem. In the sense of space P-space means all problems solvable in polynomial space can be solved in polynomial time. In the sense of time, polynomial time problems can be solved by simply traversing down the finite tree to find the solutions and then all solutions can be compared to rank them until the optimal solution is found.
Not all problems are able to be solved in this way and for example many problems cannot be solved by any algorithmic means in a reasonable amount of time. For example if a Sudoku has an infinite grid then it is not possible to solve by any algorithm in polynomial time no matter how fast you make the computer but if the grid is finite then you can solve it but it's still considered O(1) if it's a traditional finite Sudoku 9x9 grid.
P-space problems can be solved if you have unlimited time but with a polynomial amount of space. To search using binary search you need log(n) for example. This log(n) means logarithmic and it tells us how much time the algorithm would take to do the search. When optimizing algorithms we want to turn slow search time into fast search time which means to somehow take exponential time algorithms and somehow optimize them into polynomial search algorithms. Problems fit into classes so that if you can solve one problem of a certain class you solve all problems of that class. This means Sudoku is the same problem class as the Rubix cube and as Chess, but the difference maker is the size of the grid where if you make the grid big enough then all the time in the universe will not be enough to solve it even if the size of the grid is finite because of the complexity explosion effect delaying the combinatoric search process.
Non deterministic search algorithms can apply an evolutionary style or approach to search for a solution. Once a solution is found then the process can be switched from non deterministic to deterministic through cache or through saving the search. For example if you somehow had a way to try many moves on the chest board you may not be able to find the true optimal move but you can over time reach better and better moves by trial and error, by approximation, by simply playing a lot of games, and this process can over time evolve a good chess player. This is not the same as being able to map every possible move from every possible position, and it requires a lot of memory to preserve the trial and error discovery of good moves or good move patterns over time. I realize this is a very simplistic view of things and it's probably more complex but this is to illustrate what a non deterministic algorithm can do which a deterministic algorithm cannot do because you cannot solve certain problems using any deterministic means. Non deterministic polymonimal time algorithms can be solved in polynomial time through non deterministic means and while Chess for sure is a class I would consider a non-deterministic solvable problem I do not know if Chess can be solved by non-deterministic means in polynomial time which is ultimately the reason why we don't have an unbeatable chess computer even if they are very very good there may always be a computer which can be built which is a little bit better (until we max out on the hardware side).
What is Depth First Search? It is a method of searching tree like structures which TML will heavily make use of. I do not know how this relates exactly to tree extraction but I do realize the importance of the tree structure for anything involving problem solving, knowledge search, or SAT. Depth First Search can be done in O(log n) space or O(n + m).. Example code:
preorder(node v) { visit(v); for each child w of v preorder(w); } dfs(vertex v) { visit(v); for each neighbor w of v if w is unvisited { dfs(w); add edge vw to tree T } }https://www.ics.uci.edu/~eppstein/161/960215.html
The way this works is each node is visited only once. This allows for the search to be maximally efficient. Another way is to think of it as
Recall on Github it is mentioned that Ohad will be implementing "Cycle detection" along with tree extraction. If a graph contains cycles then we may reach the same node more than once. Trees as far as I know don't hit any node more than once.
We can see a full example of Depth First Search code:
// C++ program to print DFS traversal from // a given vertex in a given graph #include<iostream> #include<list> using namespace std;
// Graph class represents a directed graph // using adjacency list representation class Graph { int V; // No. of vertices
// Pointer to an array containing // adjacency lists list<int> *adj;
// A recursive function used by DFS void DFSUtil(int v, bool visited[]); public: Graph(int V); // Constructor
// function to add an edge to graph void addEdge(int v, int w);
// DFS traversal of the vertices // reachable from v void DFS(int v); };
Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; }
void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Add w to v’s list. }
void Graph::DFSUtil(int v, bool visited[]) { // Mark the current node as visited and // print it visited[v] = true; cout << v << " ";
// Recur for all the vertices adjacent // to this vertex list<int>::iterator i; for (i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFSUtil(*i, visited); }
// DFS traversal of the vertices reachable from v. // It uses recursive DFSUtil() void Graph::DFS(int v) { // Mark all the vertices as not visited bool *visited = new bool[V]; for (int i = 0; i < V; i++) visited[i] = false;
// Call the recursive helper function // to print DFS traversal DFSUtil(v, visited); }
// Driver code int main() { // Create a graph given in the above diagram Graph g(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.addEdge(3, 3);
cout << "Following is Depth First Traversal"" (starting from vertex 2) \n"; g.DFS(2);
return 0; } https://www.geeksforgeeks.org/depth-first-search-or-dfs-for-a-graph/
In any case this is getting a bit too technical but the point being that depth first search is very powerful and is one of the main methods of state space search. While I cannot confirm that Ohad will implement depth first search (although it is likely), it is in my opinion going to be a necessity for TML to implement some form of state space search. Just as BDDs are a necessary data structure, and trees are necessary, it will be necessary to have a way to do search to traverse these trees and graphs which means I can predict that there will be some form of state space search implemented if it isn't being worked on.
And knowing that TML will be capable of doing state space search and knowing Tauchain will have this capability we can extrapolate some of the possible use cases of Tauchain to get an idea on the potential value it might have.