The MONA Project
For all who are interested in Monadic Second Order Logic, the Mona Project may be of interest. As some may already know, Tau developer Ohad Asor has arrived at Monadic Second Order Logic (MSOL over Graphs) as the foundation for Tau. These concepts to most people are very new and maybe you don't even know what MSOL can do, so the MONA Project is a nice introduction to MSOL.
A quote from the website says:
MONA is a tool that translates formulas to finite-state automata. The formulas may express search patterns, temporal properties of reactive systems, parse tree constraints, etc. MONA analyses the automaton resulting from the compilation and prints out "valid" or a counter-example.
MONA implements decision procedures for the Weak Second-order Theory of One or Two successors (WS1S/WS2S). The theory of one successor, known as WS1S, is a fragment of arithmetic augmented with second-order quantification over finite sets of natural numbers. Its first-order terms denote just natural numbers. The theory has no addition, since that would make it undecidable, but it has a unary operation +1, known as the successor function. WS2S is a generalization to tree structures. Since the theories are monadic second-order logics, we call our tool MONA.
Finite state automata
A finite automaton relies on input to shift through a finite amount of states. A finite state automaton is also called a finite state machine. These function as abstract mathematical models of computation. A regular expression can be converted to a finite state automaton where the regular expression becomes states and edges.
Finite languages (regular languages)
All finite languages are context free. And finite languages are regular language. What is a regular language?
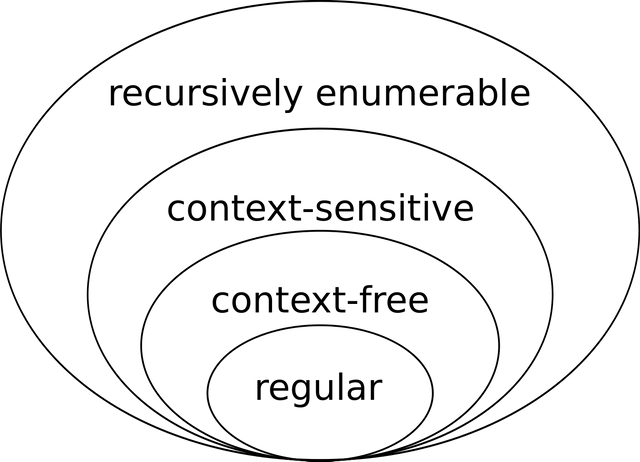
Regular languages are below context free on the Chomsky hierarchy. The Chomsky hierarchy is a containment hierarchy of classes of formal grammars. What are formal grammars? A formal grammar is a set of production rules for for strings in a formal language.
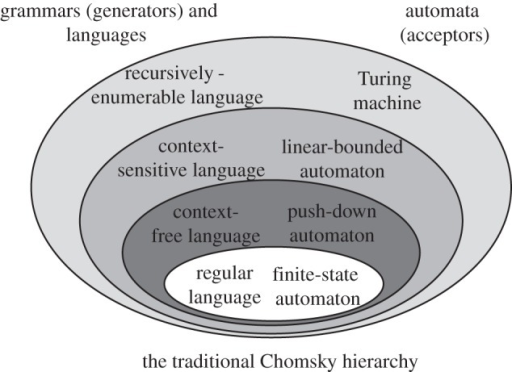
What is a formal language? A formal language is a set of strings of symbols which which may be constrained by rules specific to it. A programming language is a formal language. So we can see that Chomsky hierarchy applies to formal languages, and it includes programming languages.
Lessons:
- Finite languages are always regular.
- Infinite languages can sometimes be regular but are not always regular.
- Monadic Second Order Logic (Second Order Logic is restricted to Unary Relationships).
- A regular expressions can be converted to a finite state automaton.
- Input security is gained by language analysis, langsec, etc.
Publications
Their website offers a publications section for people who want to understand the concepts. I suggest everyone look at that section and some of the publications will be summarized by their abstracts below:
Jesper G. Henriksen, Jakob Jensen, Michael Jørgensen, Nils Klarlund, Robert Paige, Theis Rauhe, and Anders Sandholm
Abstract
The purpose of this article is to introduce Monadic Second-order Logic as a practical means of specifying regularity. The logic is a highly succinct alternative to the use of regular expressions. We have built a tool MONA, which acts as a decision procedure and as a translator to finite-state automata. The tool is based on new algorithms for minimizing finite-state automata that use binary decision diagrams (BDDs) to represent transition functions in compressed form. A byproduct of this work is an algorithm that matches the time but improves the space of Sieling and Wegener's algorithm to reduce OBDDs in linear time.
The potential applications are numerous. We discuss text processing, Boolean circuits, and distributed systems. Our main example is an automatic proof of properties for the ``Dining Philosophers with Encyclopedia'' example by Kurshan and MacMillan. We establish these properties for the parameterized case without the use of induction.
Our results show that, contrary to common beliefs, high computational complexity may be a desired feature of a specification formalism.
Abstract
In this note, we describe how a fragment of arithmetic can be decided in practice. We follow essentially the ideas of [Thatcher & Wright], which we have embedded in the Mona tool.
Mona is an implementation of Monadic Second-order Logic on finite strings (and trees). The previous semantics used in Mona is the one provided in current literature [Straubing, Thomas], where the meaning of first-order terms is restricted to being a position in the string over which the formula is interpreted.
In this note, we describe our new semantics, where terms are interpreted relative to all natural numbers. With this semantics Mona becomes a decision procedure for the calculus called WS1S, the Weak Second-order theory of 1 Successor.
We also show how the Mona representation of automata subsumes a recent proposal for representing queues. We exploit the natural semantics to carry out automated reasoning about queue operations.
References
- http://www.brics.dk/mona/
- https://www.cs.rochester.edu/u/nelson/courses/csc_173/fa/fa.html
- https://en.wikipedia.org/wiki/Chomsky_hierarchy
- https://en.wikipedia.org/wiki/Formal_grammar
- https://en.wikipedia.org/wiki/Formal_language
- https://cs.stackexchange.com/questions/6609/infinite-language-vs-finite-language
wow amazing the mona project you very good. good luck sir
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
@dana-edwards Very interesting! Thank you for sharing! :)
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Can not understand completely
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Sounds complicated. Math to me is just a more complicated way of describing the world than regular languages.
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Content reads like ancient Mandarin to me, but hey, alwways keep expanding your mind!
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
danke
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit
Thank you for the fantastic explanantion
Downvoting a post can decrease pending rewards and make it less visible. Common reasons:
Submit